§ 1.2. Уравнение Эйлера-Лагранжа.

Как показывает практика, в теории оптимального управления наиболее распространенной формой критерия оптимизации является интегральный функционал. Значение функционала определяется формой кривой подынтегральной функции. Функция, экстремизирующая функционал, называется экстремалью. Решение задачи определения экстремали было дано математиком Эйлером в середине XVIII века [2]. Аппроксимируя подынтегральные кривые ломаными, Эйлер вывел дифференциальное уравнение второго порядка, которому должны были удовлетворять экстремали. Впоследствии Лагранж назвал это уравнение уравнением Эйлера. В дальнейшем перед математиками встал вопрос решения более сложной задачи. Требуется определить экстремаль функционала при наличии ограничений в виде равенств, которым должна удовлетворять экстремаль. При решении этой задачи исследователи применили правило множителей Лагранжа, что позволило получить необходимые условия, которым должна удовлетворять искомая экстремаль. При этом уравнение Эйлера вошло в эти условия как составная часть. Далее рассмотрим вывод необходимых условий экстремума функционала при ограничениях в виде дифференциальных уравнений объекта, для которого решается задача оптимизации. Эти ограничения называются уравнениями связи. Однако прежде чем перейти к изложению вывода, напомним некоторые сведения, характеризующие понятие и свойство функционала [4].

1.2.1. Определение функционала. Если каждой функции из множества поставлено в соответствие по некоторому правилу число , то говорят, что на множестве (в классе ) определен функционал . Множество функции (класс функций ), на котором определен функционал , называется областью задания функционала.

Вариация аргумента функционала. Вариацией или приращением аргумента функционала называется разность между двумя функциями и из выбранного множества :

, .

Кривые и , заданные на отрезке , близки в смысле близости нулевого порядка, если модуль разности для , где - малая величина. Геометрически это означает, что кривые при близки по ординатам. Если для этих же кривых и при (где обозначено ), то кривые близки в смысле близости первого порядка. Геометрически это означает, что кривые при близки как по ординатам, так и по направления касательных в соответствующих точках. Кривые и близки в смысле близости -го порядка, если выполняются неравенства:

, ,…

при . Если кривые близки в смысле близости -го порядка, то они тем более близки в смысле близости любого меньшего порядка.

Непрерывность функционала. Функционал , определенный на множестве функции , называется непрерывным на элементе множества в смысле близости -го порядка, если для любого числа существует число , такое, что для всех допустимых функций , удовлетворяющих условиям

, ,…

выполняется неравенство . Функционал, не являющийся непрерывным смысле близости -го порядка, называется разрывным в смысле названной близости.

Приращение функционала. Приращением функционала , отвечающим приращению аргумента , называется величина:

Дифференцируемость функционала. Вариация функционала. Функционал , заданный на множестве , называется дифференцируемым в точке , если существует такой линейный относительно приращения аргумента функционал , что для любого допустимого приращения функции приращение функционала имеет вид:

и

При этом называется сильным дифференциалом (дифференциал Фреше) функционала или его первой вариацией и обозначается

(1.16)

Экстремум функционала. Если в окрестности точки функционального пространства , где , разность сохранят знак, то функционал имеет локальный экстремум на кривой . Если неравенство выполняется для всех кривых функционального пространства определения функционала, то на кривой достигается абсолютный максимум. Аналогично, если справедливо неравенство для всех кривых , то на кривой достигается абсолютный минимум.

Теорема 1.4. Необходимое условие экстремума функционала. Если дифференцируемый функционал имеет экстремум на , где - внутренняя точка области определения функционала, то на кривой выполняется неравенство

(1.17)

Функции, для которых , называют стационарными функциями или стационарными точками функционального пространства задания функционала [4].

Основная лемма вариационного исчисления. Если функция , заданная на отрезке , непрерывна и для любой непрерывной функции , заданной на отрезке , имеет место равенство

, то

1.2.2. Вывод уравнения Эйлера-Лагранжа. Рассматривается задача Больца с закрепленными концами и безусловными ограничениями в виде дифференциальных уравнений связи. Исходные данные имеют следующий вид:

критерий оптимизации функционал

уравнения связи (уравнения объекта) ; (1.18)

граничные условия: , .

Функции являются непрерывными и дифференцируемыми (принадлежат пространству ), функция - непрерывная (принадлежит пространству ). Постановка задачи оптимизации:

определить ,

На основании метода Лагранжа перейдем от решения оптимизационной задачи на условный экстремум функционала (при наличии ограничений в виде уравнений связи) к задаче на безусловный экстремум. Для этого составим лагранжиан:

(1.19)

где - непрерывная вектор-функция множителей Лагранжа.

Поскольку ограничения в виде уравнений объекта (1.18) должны быть выполнены в любой момент времени , что фактически означает наличие бесконечного числа ограничений, числовые множители Лагранжа представляются функцией времени.

От первоначальной задачи переходим к задаче:

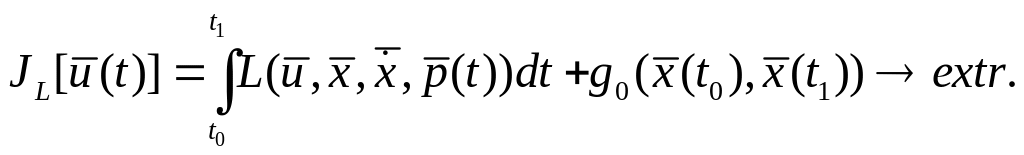(1.20)

Предположим, что оптимальное управление найдено. Следовательно, определена оптимальная траектория САУ , на которой функционал (1.20) достигает экстремума. Рассмотрим его приращение за счет малой - вариации оптимального уравнения и соответствующей ей вариации траектории системы . Так как функции и являются гладкими, малые вариации управления дают и малые вариации значения функционала . Допустим, что функция непрерывна по совокупности своих аргументов и имеет непрерывные частные производные второго порядка по всем аргументам в области , , , . Приращение функционала , отвечающее приращению аргумента, где имеет вид

(1.21)

В постановке оптимизационной задачи концы траектории закреплены, вариация траектории на концах недопустима, поэтому терминантный член функционала (функция ) отсутствует в выражении (1.21). Представим разность функций под интегралом (1.21) в виде разложения Тейлора, что допустимо вследствие непрерывности функции

(1.22)

где - остаточный член разложения ряда Тейлора. После подстановки (1.22) в (1.21) получим

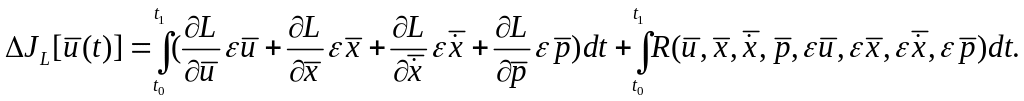(1.23)

Первое слагаемое в правой части (1.23) линейно относительно и . Пусть все вторые частные производные функции по , , и не превосходит по абсолютной величине некоторой константы . Выберем таким образом, чтобы была справедлива оценка:

(1.24)

Здесь . Следовательно, второе слагаемое в правой части (1.22) – второго порядка малости относительно и согласно определению функционал является дифференцируемым в пространстве и его первая вариация имеет вид:

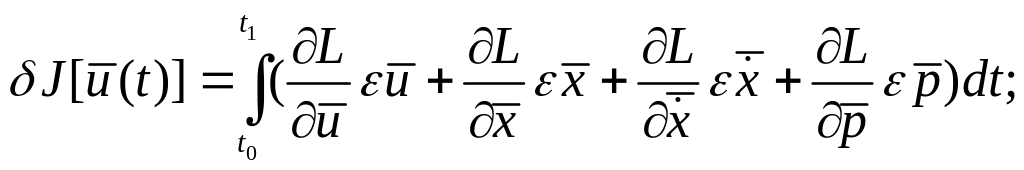(1.25)

где , , - векторы вариации траектории, управления и множителей Лагранжа соответственно. В результат интегрирования по частям третьего слагаемого в (1.25) имеем:

(1.26)

Первое слагаемое в (1.26) равно нулю, так как концы закреплены, и вариация траектории на концах исключается . С учетом (1.25) и (1.26) необходимое условие экстремума функционала (1.20) имеет вид:

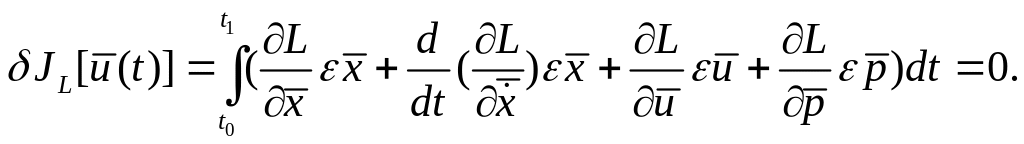(1.27)

В связи с тем, что вариации переменных в (1.27) произвольны, условие может быть выполнено, если интеграл от каждого слагаемого равен нулю. Тогда согласно основной лемме вариационного исчисления можно записать:

, , (1.28)

Если учесть выражение для лагранжиана (1.19) то система (1.28) примет вид:

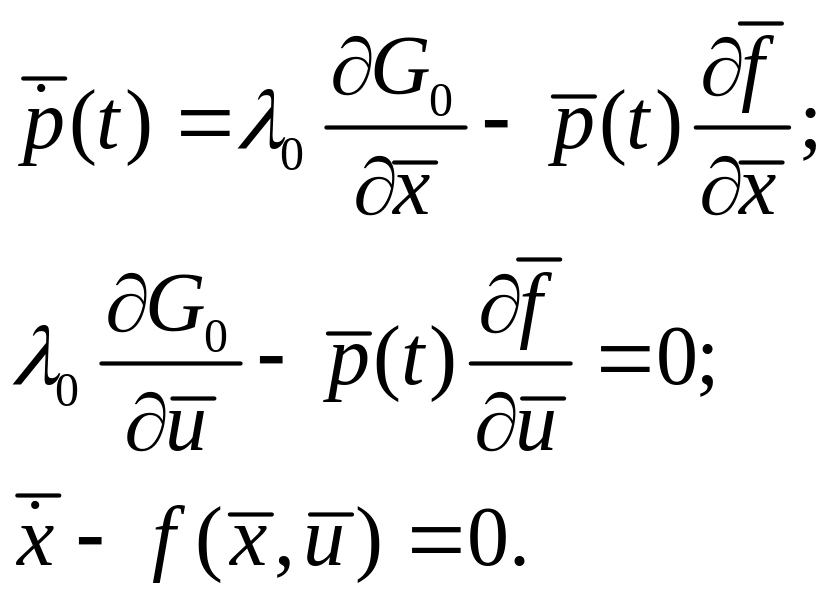(1.29)

Система уравнений (1.28) представляет собой необходимые условия экстремума функционала (1.20) при наличии ограничений в виде уравнений связи и называется уравнениями Эйлера-Лагранжа. Набор условий, который содержит система (1.28 или 1.29) является полным для определения всех неизвестных функций , , . Всего неизвестных функций _, для их определения имеется уравнений. Выражая из второго (когда это возможно) через и , получаем систему из скалярных дифференциальных уравнений. Ее решение зависит от произвольных постоянных. В задачах с закрепленными концами для их определения имеется граничных условий. Таким образом, число неизвестных совпадает с числом уравнений. Однако, возможность разрешимости полученной системы уравнений относительно искомых переменных зависит от формы исходных данных.

Теперь рассмотрим необходимые условия для задачи оптимизации со свободным правым концом (значение не задано). В такой постановке допускается вариация значения , и поэтому первая вариация функционала может быть представлена в виде:

Необходимое условие экстремума согласно необходимому условию экстремума функционала (1.17) в этом случае содержит уравнения равенства в виде (1.28), а также следующие соотношения:

(1.30)

Уравнение (1.30) называется условиями трансверсальности для свободного правого конца траектории. Подобное соотношение может быть написано для левого конца траектории, если он не закреплен. Условия трансверсальности восполняют недостаток информации за счет потери граничных условий при свободных концах траектории.

Для решения многих задач более удобной является другая форма представления системы (1.28), которая называется канонической. Определим скалярную функцию – гамильтониан:

В отличие от лагранжиана не содержит слагаемого , поэтому

Отсюда

Каноническая форма системы (1.28) имеет вид:

, (1.31)

Очевидно, система (1.31) содержащая два векторных уравнения, эквивалентна двум уравнениям системы (1.28) Далее рассмотрим применение полученных теоретических положений для решения практических задач.

Пример 1. Требуется определить оптимальную траекторию движения объекта при следующих исходных данных [6]:

описание движения объекта

краевые условия ,

критерий оптимизации

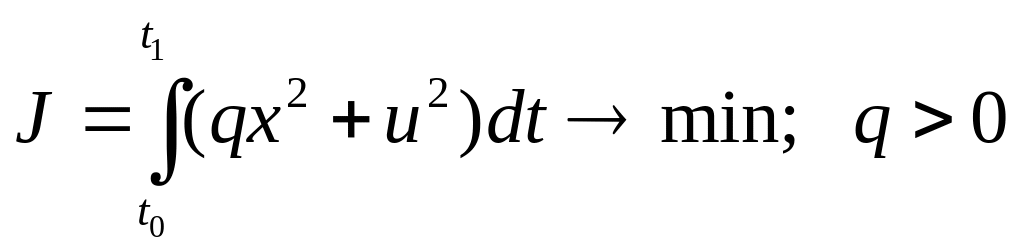
Для решения задачи составим лагранжиан:

причем и выпишем необходимые условия экстремума функционала:

стационарность по :

стационарность по :

Полученные уравнения позволяют выразить функцию управления через и исключить затем ее из уравнения связи:

Из последнего уравнения выразим множитель , затем продифференцируем его по времени и подставим , в уравнение стационарности по :

Решение этого уравнения:

,

Неизвестные коэффициенты можно определить из краевых условий:

Пример 2. Задача синтеза оптимального регулятора [5]. Требуется определить структуру регулятора, который обеспечивал бы оптимальный режим движения объекта, передаточная функция которого имеет вид колебательного звена:

В пространстве состояний динамика колебательного звена описывается системой уравнений:

Рассматривается режим отработки ненулевых начальных условий, что соответствует задаче с закрепленными концами:

,

Критерий оптимизации имеет вид:

где , , - некоторые весовые коэффициенты. Для решения задачи синтеза регулятора нужно найти уравнение, связывающее управляющий сигнал и переменные состояния и . Для решения задачи формируется лагранжиан при :

Система уравнений Эйлера-Лагранжа имеет вид:

Из последнего уравнения системы можно выразить управляющее воздействие:

и, подставив во второе уравнение связи, получим систему уравнений:

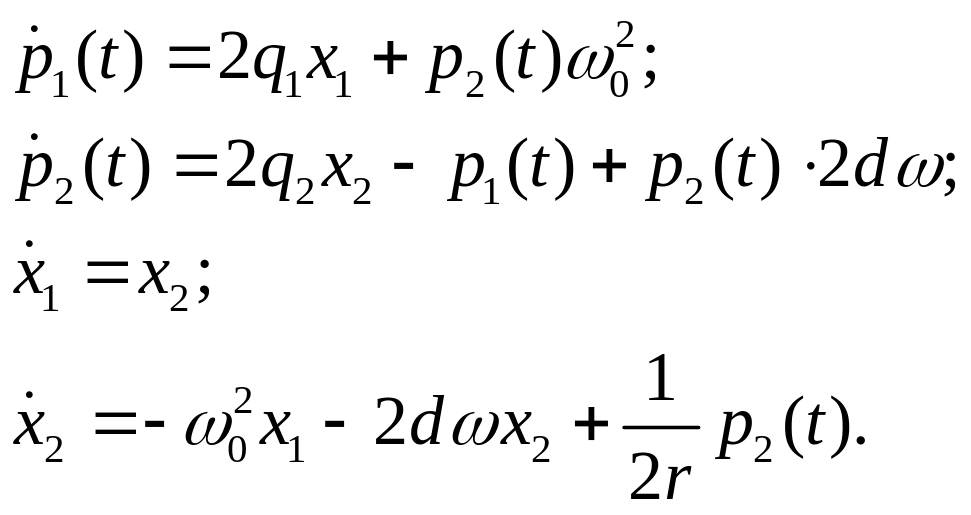
Характеристическое уравнение этой системы:

Обозначим ,

Тогда расположение корней характеристического уравнения на комплексной плоскости будет определяться соотношением между и . При и все корни характеристического уравнения чисто мнимые и оптимального регулятора не существует. При и корни действительные:

,

где , ,

и решение системы уравнений для переменной можно представить

На основании краевых условий для произвольные постоянные и, следовательно,

Из последних соотношений определяются постоянные и через и :

,

и вторая производная по времени для выходной переменной колебательного звена:

Теперь из второго уравнения системы уравнений связи можно получить уравнение регулятора:

Таким образом, регулятор оптимизации движения объекта управления в виде колебательного звена для критерия в виде имеет структуру из параллельно соединенных пропорционального и дифференцирующего звеньев с коэффициентами передачи соответственно и :

Рис. 1.1.

При корни характеристического уравнения будут комплексными. Структура регулятора не изменится, но коэффициенты передачи будут иметь другое значение.