Глава II: Варианты построения адаптивных систем. §4. Адаптивная система с определением градиента методом вспомогательного оператора, содержащая настраиваемую модель (идентификационного типа).

Согласно заголовку параграфа рассматривается АдСУ идентификационного типа [12]. Текущие параметры регулятора определяются с использованием беспоискового алгоритма вычисления текущих значений градиента функционала качества в пространстве вектора . Контур адаптации содержит настраиваемую модель объекта управления (ОУ), представленную оператором . Структурная схема системы изображена на рис.2.1.

Рис. 2.1

Рассматривается пример один вход и один выход. Структура регулятора основного контура известна и на рисунке обозначена в виде оператора R с параметрами в форме вектора , которые настраиваются в процессе работы АдСУ. В алгоритмах настройки параметров регулятора используется текущая измерительная информация в основном контуре о значении переменных и оценки текущих и неизвестных параметров ( объекта управления заданного оператором . Для вычисления оценок используется настраиваемая модель с оператором W_M( ,эквивалентным оператору объекта управления . Математическое описание основного контура в операторной форме имеет вид:

(2.1)

Для настройки параметров регулятора выбирается критерий качества управления в виде функции , где - функция обобщенной ошибки адаптивного управления, задаваемая аналитически. При условии отсутствия ограничений на изменение вектора , оптимальное значение этого вектора определяется на основании необходимого условия безусловного экстремума критерия качества , что значит .

При значениях , где параметры регулятора обеспечивают минимальное значение критерия качества, . Принимая во внимание, что значение выходной переменной зависит от параметров регулятора , выражение для частной производной по можно записать:

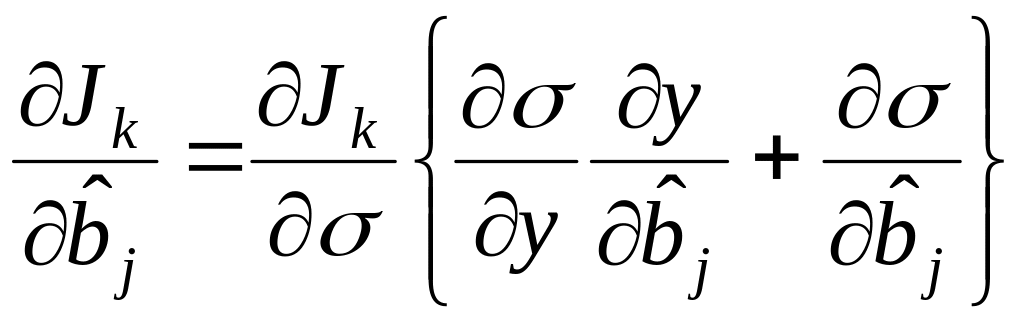(2.2)

Для вычисления значений производных проводим по уравнению (2.1):

, (2.3)

На основании (4.3) можно получить соотношение для вычисления производных : 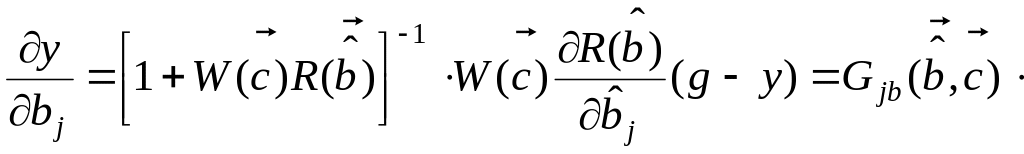e (2.4)

Скалярную функцию называют вспомогательным оператором (фильтр ). В соответствии с (2.4) компоненты градиента критерия вычисляются в общей аналитической форме.

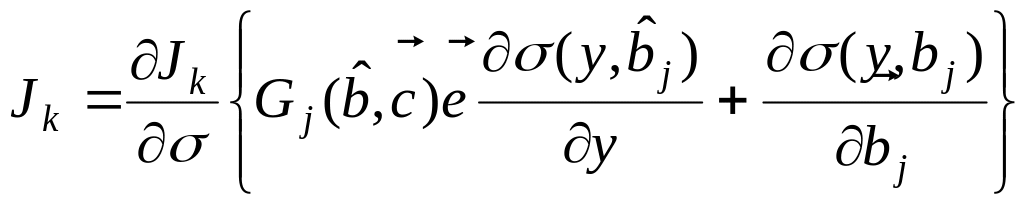(2.5)

При выбранных начальных значениях алгоритм настройки параметров с использованием вычисляемых текущих значений градиента в соответствии с (2.5) при использовании алгоритма градиентного спуска имеет вид

(2.6)

Согласно способу вычисления градиента на основе оператора и алгоритма градиентного спуска, метод построения адаптивной системы получил название метод вспомогательного оператора. Основной недостаток метода заключается в необходимости иметь точную априорную информацию о математической модели ОУ. Если изменение параметров в процессе функционирования невелико, то можно взять среднее значение составляющих вектора . Но основное использование метода вспомогательного оператора предполагает наличие в АдСУ настраиваемой модели, т.е. предполагает реализацию структуры и алгоритмов системы, изображенной на рис. 4.1.

Для определения значений оценок составляющих целесообразно применение также алгоритма градиентного спуска и метода вспомогательного оператора. Решение задачи идентификации объекта управления, представленного оператором , осуществляется на основании критерия оптимизации как функции рассогласования выходных переменных ОУ и модели: , где - невязка, определяющая степень отличия оператора модели и оператора ОУ . Значения оценок вектора определяются на основе экстремизации функции от невязки по аналогии с вышеописанной вычислительной процедурой определения оценок параметров регулятора . Частная производная для по оценке

, где (2.7)

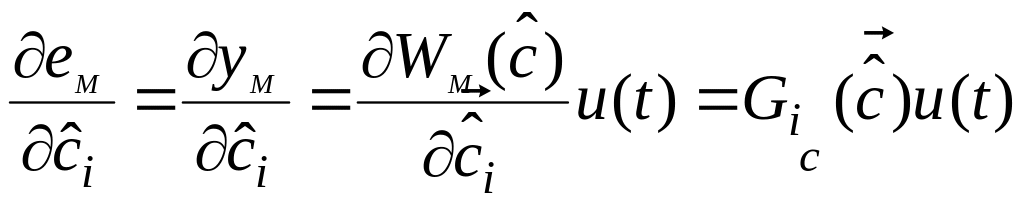
В выражении (2.7) скалярная функция - вспомогательный оператор или функция чувствительности оператора настраиваемой модели к изменениям оценок . Следовательно, градиент критерия имеет вид:

Алгоритм вычисления оценок вектора окончательно записывается в форме:

(2.8)

Для определения оценок согласно (2.8) необходимо задать начальное значение оценок и выбрать значение коэффициента >0 из условия сходимости и качества процедуры (2.8). Значение раскрывается в явной аналитической форме. Полная структурная схема АдСУ, построенная в соответствии с уравнениями (2.1, 2.5, 2.6, 2.8) изображена на рис.2.1, где двойными линиями отображаются векторные связи и многомерность вычислительных алгоритмов.

При решении конкретной задачи синтеза АдСУ на основании вышеописанных вычислительных процедур операторы регулятора, ОУ и модели следует представить в виде передаточных функций. Следует заметить, что функционирование системы может осуществляться в нестационарном режиме, когда скорость изменения параметров и сопоставима со скоростью изменения переменных .Это объясняется непрерывностью вычислений, проходящих в темпе протекания процессов в контурах системы. Однако гарантировать достижимость цели адаптивного управления в таких случаях без дополнительных условий (например, с использованием функций Ляпунова) нельзя.