Закономірність розподілу та його форми
Розглядаючи РР неважко помітити певні залежності між змінами значень ознаки (варіантами) та частотами:
частоти зі збільшенням значень ознаки спочатку збільшуються до певної max величини, а потім приблизно з середини ряду – зменшуються.
Закономірності зміни частот у варіаційних рядах у зв’язку зі зміною варіаційної ознаки називається закономірністю розподілу.
Законом розподілу виражаються властивості явищ, загальні умови і основні фактори, що впливають на формування варіації ознаки.
Тому однією із найважливіших задач аналізу РР є: виявлення закономірності розподілу, визначення її форми, типу та кількісного виразу.
Формою розподілу називається крива, що виражає закономірність розподілу одиниць сукупності за величиною варіюючої ознаки.
Розрізняють емпіричні та теоретичні криві розподілу.
Емпірична – це фактична крива розподілу (полігон або гістограма), що побудована за даними статистичного спостереження, в якій відображаються як загальні, так і випадкові фактори.
Теоретична – це крива, яка виражає функціональний зв'язок між змінами варіаційної ознаки і частотами, та характеризує певний тип роподілу.
Криві розподілу за формою бувають одно-, дво- та багатовершинними.
Для однорідних сукупностей характерні, як правило, одновершинні розподіли.
Наявність 2-х і більше вершин свідчить про неоднорідність сукупності.
Одновершинні бувають симетричними та асиметричними. В залежності від того, яка гілка кривої розподілу витягнута – права чи ліва, розрізняють правосторонню чи лівосторонню асиметрію.
Характеристика форм розподілу
Найпростішою
мірою асиметрії є відхилення між
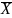, Ме, Мо.
У симетричному (нормальному) розподілі: =Мe= Мo, а R=6σ; σ=1,25 .
При правосторонній асиметрії >Ме> Мо.
При лівосторонній <Ме< Мо.
Тобто у симетричному ряді розподілі рівновіддалені від центру значення ознаки мають однакові частоти.
Для характеристики 2-х або декількох рядів використовується коефіцієнт асиметрії (А):
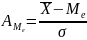або
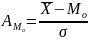
Якщо А>0 – правостороння асиметрія;
А<0 – лівостороння;
А=0 – симетричний розподіл.
Чим ближчий чисельник коефіцієнта (А) до нуля, тим менша асиметрія.
Графіки
Криві розподілу мають різну гостровершинність. Крутизна, гостровершинність або пологовершинність кривої розподілу називають ексцесом.
Розрізняють ексцеси: нормальний, вище нормального, нижче нормального.
Рис.
Для характеристики ексцесу застосовується коефіцієнт ексцесу, який розраховується на базі центральних моментів розподілу (ЦМР).
ЦМР – це середнє арифметичне k–го ступеня відхилення варіантів ознаки від їх середньої величини.
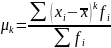
Тоді при k=0 отримаємо ЦМР нульового порядку.
При k=1 отримаємо ЦМР І-го порядку = 0.
При k=2 – ЦМР ІІ-го порядку = дисперсії.
k=3, ЦМР – характеризує асиметрію і використовується при розрахунку стандартизованого коефіцієнту асиметрії (відношення ЦМР ІІІ-го порядку до СКВ у кубі).
При
правосторонній асиметрії
,
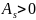лівосторонній
асиметрії
,
в
симетричному розподілі
.
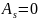Цей показник асиметрії більш точний, ніж попередні і застосовується більш широко.
Вважається,
що при
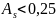асиметрія незначна.
При
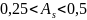– середня.
При
– значна.
ЦМР IV-го порядку використовується для характеристики ексцеса (при розрахунку коефіцієнта ексцеса):
Якщо розподіл нормальний (симетричний), то ексцес – нормальний Е=3.
При: Е>3 – вище нормального (гостровершинний);
Е<3 – нижче нормального (плосковершинний).
Розглянуті характеристики варіаційних рядів допомагають більш детально вивчити особливості статистичних сукупностей та їх закономірності.
Висновок: При вивченні даної теми потрібно звернути особливу увагу на той факт, що в аналітичній роботі не можна обмежуватися обчислювачем і аналізом середніх величин. Якісний аналіз не можливий без вживання показників варіації, які дають не менше цінну інформацію про вивчення явища, ніж середні величини.