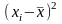Тема 6. Показники варіації та закономірність розподілу

1. Поняття варіації та її основні показники.

2. Дисперсія, її різновиди, властивості та взаємозв’язок дисперсій.

3. Закономірність розподілу та його форми.

4. Характеристика форм розподілу

1. Поняття варіації та її основні показники

Для повноти аналізу і кращого обґрунтування його результатів використовують показники варіації.

Варіація (від лат. variatio) – зміна значень ознаки у одиниць сукупності в один і той же момент або період часу.

У статистико-економічному аналізі застосовуються такі показники варіації:

1) розмах варіації – (R).

2) середнє лінійне відхилення – ( ).

3) дисперсія (середній квадрат відхилень) – ( ).

4) cереднє квадратичне відхилення – (σ).

5) коефіцієнт варіації – ( ).

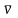Варіаційний розмах (амплітуда коливань) є найпростішим показником варіації ознаки. Обчислюється як різниця між найбільшим і найменшим значеннями кількісної ознаки в деякій сукупності.

Їх сутність та методи обчислення розглянемо на простому ПРИКЛАДІ:

Є дані про виробіток робітниками 2-х бригад, у складі 5-и чоловік:

№ з/п	I бр.	II бр.
1	8	4
2	2	5
3	3	4
4	5	3
5	2	4
Всього	20	20

Тоді середній виробіток по бригадах:

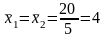
Яку із бригад доцільно найняти для виконання робіт? Адже середній виробіток у них однаковий?

Обчислимо показники варіації:

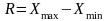, (1)

де 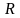– розмах варіації;

– найбільше значення ознаки;

– найменше значення ознаки.

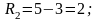
Отримані дані свідчать, що II бригада більш однорідна за виробітком і класифікацією.

Простота підрахунку розмаху варіації сприяє його широкому застосуванню в теоретичних дослідженнях і практичних розрахунках.

Разом з тим цей показник має істотний недолік: він не дає уявлення про ступінь коливання ознаки всередині сукупності, оскільки обчислюється на основі тільки двох крайніх значень ознаки. Ці ознаки можуть мати випадкові характеристики, не типові для даної сукупності. Тому цей показних використовується для попередньої, орієнтовної оцінки варіації.

Більш досконалим показником, який враховує відхилення значення кожної ознаки від середньої є середнє лінійне відхилення (СЛВ)

Воно є середньою арифметичною з відхилень окремих абсолютних значень ознаки від їх середнього значення. Може бути простим і зваженим.

Просте середнє лінійне відхилення обчислюється за формулою

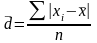, (2)

де – середнє лінійне відхилення;

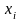– конкретне значення варіанта ознаки;

– середнє значення ознаки;

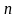– число варіантів.

Для варіаційного ряду обчислюють зважене СЛВ:

. (3)

ПРИКЛАД.

Табельний номер робітника	I бр.				II бр.
1	8	4	16	4		0	0
2	2	2	4	5		1	1
3	3	1	1	4		0	0
4	5	1	1	3		1	1
5	2	2	4	4		0	0
Всього:	20	10	26	20		2	2

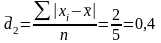шт. шт.

Отже, в середньому виробіток робітників I бригади відхиляється від середньої на 2 шт. Тобто, II бригада більш однорідна.

Варіаційний розмах і СЛВ були єдиними вимірниками варіації на початку розвитку теорії статистики.