Міністерство освіти, науки, молоді і спорту України
Педагогічний коледж
Чернівецького національного університету ім. Ю.Федьковича
Схвалено методичною радою
Педагогічного коледжу
Чернівецького національного
університету ім. Ю.Федьковича
Протокол № 4 від 21.11.2012
Русакова О.Я.
Короткий курс лекцій з методики навчання математики
Частина 2. Текстові задачі
Навчально-методичний посібник
Електронна версія
Для студентів педагогічних навчальних закладів І – ІІ рівня акредитації та вчителів початкових класів
Розглянуто на засіданні
предметно-циклової комісії
викладачів математики, фізики,
основ інформатики, ТЗН
Протокол № 3 від 18.10.2012
Чернівці
2012
Зміст
Лекція 1. Сюжетні задачі як особлива частина змісту початкового курсу математики . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Лекція 2. Види простих задач та їх класифікація. Деякі особливості формування в учнів умінь розв’язувати прості задачі. Ознайомлення з оберненою задачею . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Лекція 3. Методика навчання учнів розв’язування складених задач . . . . . . 14
Лекція 4. Методика навчання розв’язування типових задач . . . . . . . . . . . . . 20
Список рекомендованої літератури . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
Лекція 1. Сюжетні задачі як особлива частина змісту початкового курсу математики
Додаток 2 до Державного стандарту
ДЕРЖАВНІ ВИМОГИ до рівня загальноосвітньої підготовки учнів
Зміст початкової загальної освіти |
Державні вимоги до рівня загальноосвітньої підготовки учнів |
Задача. Структура задачі. Загальні прийоми роботи із задачею
|
Учень повинен мати уявлення про сюжетну задачу, виділяти її структурні компоненти; проводити семантичний аналіз тексту задачі та подавати його результати у вигляді схеми, рисунка, таблиці; складати план розв’язання складеної задачі, пояснювати вибір дій; записувати розв’язання задачі діями з поясненням, виразом або рівнянням; знаходити різні способи розв’язування задачі, визначати раціональний, перевіряти правильність розв’язання задачі; складати задачі за рисунком, схемою, математичним виразом, за практичними діями з предметами, задачі, аналогічні та обернені до розв’язаної |
Прості і складені задачі |
Учень повинен вміти розв’язувати прості сюжетні задачі, що розкривають зміст арифметичних дій, задачі на знаходження невідомого компонента дій, задачі, які містять відношення різницевого та кратного порівняння, задачі на знаходження частини від числа або числа за його частиною, задачі з пропорційними величинами; розв’язувати складені задачі, що є композицією з двох-чотирьох видів простих задач, задачі на знаходження четвертого пропорційного, задачі на пропорційне ділення, на знаходження невідомого за двома різницями, на подвійне зведення до одиниці, на спільну роботу, на одночасний рух двох тіл |
Роль і місце задач у початковому курсі математики. Функції сюжетних задач
В системі навчання учнів початкових класів загальноосвітньої школи переважають арифметичні задачі, які, з одного боку, становлять специфічний розділ програми, а з другого, виступають як дидактичний засіб навчання, виховання і розвитку школярів.
Арифметичною задачею називають вимогу знайти числове значення деякої величини, якщо дано числові значення інших величин і існує залежність, яка пов’язує ці величини як між собою, так і з шуканою величиною.
Арифметичні задачі формулюють природною, тобто звичайною, мовою. Тому їх називають текстовими. А ще їх називають сюжетними, оскільки вони описують ті чи інші реальні ситуації.
Текстова задача – це опис на звичайній мові деякої ситуації, в якій потрібно дати кількісну характеристику якої-небудь компоненти цієї ситуації, встановити наявність чи відсутність певного відношення між її компонентами чи визначити вид цього відношення.
Будь-яка текстова задача складається з двох частин: умови і вимоги (питання). В умові повідомляються дані про об’єкти і деякі величини, що характеризують ці об’єкти, про відомі і невідомі значення цих величин, про відношення між ними. Вимога задачі – це вказівка того, що потрібно знайти. Ця вимога може бути сформульована як у наказовій формі (Знайдіть площу прямокутника), так і у вигляді запитання (Яка площа прямокутника?).
Текстові задачі у початковому курсі математики мають навчальні, виховні та розвиваючі функції..
Навчальні функції задач полягають у формуванні в школярів системи математичних знань, умінь та навичок, необхідних як у повсякденному житті, так і для подальшої освіти, в тому числі і при вивченні інших дисциплін.
Зміст конкретних задач дає змогу реалізовувати виховну функцію задач. Зокрема, виховуються патріотичні почуття, свідоме і бережне ставлення до навколишнього середовища, повага до батьків та їхньої праці, бережне ставлення до результатів людської праці. Крім того, розв’язування задач потребує від дитини формування у неї вольових якостей характеру таких як наполегливість, посидючість.
Розвивальна функція задач проявляється у першу чергу у формуванні в учнів вмінь виконувати різні розумові операції (аналіз, синтез, конкретизація і абстрагування, порівняння і узагальнення), чітко і лаконічно висловлювати свої судження, робити висновки. Зміст значної кількості задач сприяє формуванню в учнів наукового світогляду.
2. Способи розв’язування текстових задач а) арифметичний
Задача 1. (М. 4 (Б), № 334, с. 53) за три місяці завод випустив 4603 автомобілі. Скільки автомобілів випустив завод окремо за кожний місяць, якщо за перший і другий місяці він випустив 2978 автомобілів, а за перший і третій місяці -3093?
2-ий місяць
- ?
2978
4603 1-ий місяць - ?
3093
3-ій місяць - ?
_4603
2978
1625 (авт.) – випустив завод за третій місяць;
_4603
3093
1510 (авт.) – випустив завод за другий місяць;
_2978 або 3) _ 3093
1510 1625
1368 (авт.) 1368(авт.) – випустив завод за перший місяць.
Відповідь: за перший місяць завод випустив 1368 автомобілів, за другий – 1510, за третій – 1625.
Відповідь на запитання задачі знаходять в результаті виконання однієї чи кількох арифметичних дій над числами, заданими в умові задачі чи знайденими в процесі виконання цих дій. Цей спосіб розв’язування задач у початковому курсі математики є найпоширенішим. Якщо відповідь задачі отримуємо в результаті виконання однієї арифметичної дії, то задача називається простою. Якщо відповідь на питання задачі отримуємо в результаті двох чи більше арифметичних дій, то задача називається складеною.
б) алгебраїчний
Задача 2. У двох цистернах 5300 л бензину. В одній із цих цистерн 2598 л бензину. Скільки бензину у другій цистерні?
За умовою здачі складають рівняння, в якому за невідому величину, як правило, приймають шукану. Розв’язавши складене рівняння, отримують відповідь на запитання задачі. Розв’язання задач алгебраїчним способом у початковому курсі використовується не так часто, як арифметичним.
Розв’язання
Припустимо, що у другій цистерні х літрів бензину. Тоді у двох цистернах разом 2598 + х літрів. З умови задачі відомо, що у двох цистернах разом 5300 літрів бензину. Тому маємо таке рівняння: 2598 + х = 5300. Розв’яжемо це рівняння. (Коментар дається усно, записується тільки рівняння і його розв’язання)
2598 + х = 5300 _ 5300 + 2598
х = 5300 – 2598 2598 2702
х = 2702 2702 5300
2598 + 2702 = 5300
5300 = 5300
Відповідь: у другій цистерні 2702 л бензину.
в) геометричний
Задача 3. ( М. 4 (Б), № 626, с. 96) Два велосипедисти виїхали одночасно з міста до бази відпочинку. Один їхав зі швидкістю 10км/год, другий – 13км/год. Через дві години другий велосипедист проколов камеру, тому далі йшов пішки зі швидкістю 4км/год. На якій відстані від міста перший велосипедист дожене другого?
Інтерпретуючи величини відрізками і дотримуючись масштабу, знаходять відповідь на запитання задачі.
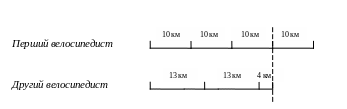
З малюнка-схеми видно, що перший велосипедист наздожене другого в кінці третьої години від початку руху. Це буде на відстані 10км · 3 = 30км. Перевіряємо, що другий велосипедист за цей же час пройде також 30км (13км + 13км + 4км = 30км).
Спосіб ефективний тим, що задіяне наочно-образне мислення, яке переважає у молодших школярів. Але задач, що можуть бути розв’язані чисто геометричним способом, у початковому курсі математики дуже мало. Проте варто зауважити, що є випадки, коли геометрична ілюстрація є одним із кроків до встановлення іншого, нестандартного, способу розв’язання деяких задач, наприклад, такої.
Задача 4. Для дитячого садка купили 63 червоних кульки, зелених – на 17 менше, ніж червоних, а синіх – на 29 менше, ніж зелених. Скільки купили синіх кульок?
Розв’язання
Спосіб 1.
1) 63 – 17 = 46 (к.) – зелених;
2) 46 – 29 = 17 (к.) – синіх.
Спосіб 2.
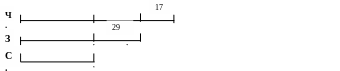
1) 17 + 29 = 46 (к.) – на стільки менше синіх, ніж червоних;
2) 63 – 46 = 17 (к.) – синіх.
Відповідь: Купили 17 синіх кульок.
Лекція 2. Види простих задач та їх класифікація. Деякі особливості формування в учнів умінь розв’язувати прості задачі. Ознайомлення з оберненою задачею.
А) Задачі, що розкривають зміст дій
а) Задача на знаходження суми, розкриває зміст дії додавання
У кошику лежало троє кошенят. Неподалік гралося ще двоє. Скільки кошенят було у мами-кицьки?
3 к. 2
к.
?
3 + 2 = 5 (к.).
Відповідь: було 5 кошенят.
Або
У вазі лежало 6 цукерок. Мама поклала ще 3. Скільки цукерок стало у вазі?
Було – 6 ц.
Поклала – 3 ц.
Стало – ?
6 + 3 = 9 (ц.).
Відповідь: стало 9 цукерок.
б) Задача на знаходження остачі, розкриває зміст дії віднімання
У дворі гралося 5 кошенят. Одне кошеня відбігло. Скільки кошенят залишилося?
Було – 5 к.
Відбігло – 1 к.
Залишилося ?
5 – 1 = 4 (к.).
Відповідь: залишилося 4 кошенят.
Ознайомлення із задачею проводиться якраз через цих два перших види задач. Учні повинні добре усвідомити структуру задачі (де умова, де запитання), розрізняти розв’язок задачі і відповідь. На перших порах і у підручнику, і в зошитах з друкованою основою на це звертається особлива увага, зроблені відповідні записи.
При навчанні розв’язування цих задач звертається увага ще і на такі моменти: якщо ми об’єднуємо (приєднуємо) множини (групи) предметів, то задача розв’язується дією додавання; якщо ми забираємо (вилучаємо) частину предметів, то задача розв’язується дією віднімання.
Варто вчити учнів також знаходити ті слова, які є визначальними для вибору дії. Наприклад у задачі «Відрізали 2 м стрічки, а потім ще 3 м. Скільки всього метрів стрічки відрізали?» визначальним є не слово «відрізали», а слово «всього».
в) Задача, що розкриває зміст дії множення
У пакет вміщується 5 яблук. Скільки яблук можна покласти у 7 таких пакетів?
7 п. по 5 ябл., ? ябл.
Для того, щоб діти краще усвідомили зміст дії множення, на перших порах розв’язання задачі записують спочатку дією додавання, а нижче – відповідною дією множення.
5 + 5 + 5 + 5 + 5 + 5 + 5 = 35 (ябл.).
5 · 7 = 35 (ябл.).
Відповідь: у 7 пакетах 35 яблук.
г) Перша задача, що розкриває зміст дії ділення – ділення на рівні частини
12 морквин розділили порівну на 3 пучки. Скільки морквин клали в один пучок?
12 м. у 3 п. по ? м.
12 : 3 = 4 (м.).
Відповідь: в одному пучку 4 морквини.
д) Друга задача, що розкриває зміст дії ділення – ділення на рівні частини
12 морквин розділили на пучки, беручи у кожний по 3 морквини. Скільки вийшло пучків?
12 м. у ? п. по 3 м.
12 : 3 = 4 (п.).
Відповідь: вийшло 4 пучки.
При ознайомленні з цією парою задач варто проілюструвати ситуації, що описуються в задачах, відповідними діями з лічильним матеріалом. При діленні на рівні частини морквини розкладаємо по одній по черзі на кожен із трьох пучків, рахуємо кількість морквин, що припадає на кожний пучок. При діленні на вміщення морквини розкладаємо по три, рахуємо кількість пучків.
Особливу увагу заслуговує задача на ділення на вміщення. Учні часто не можуть визначити правильно, яке найменування слід дати числу-відповіді. Тому щоразу треба наголошувати на те, про що запитується у відповіді.
Б) Задачі, що розкривають новий зміст арифметичних дій
а) Задача на збільшення на кілька одиниць, пряма форма
У Михайлика було 5 марок, а у Сергійка на 2 марки більше. Скільки марок було у Сергійка?
М. – 5 м.
С. – ?, на 2 м. більше
5 + 2 = 7 (м.).
Відповідь: у Сергійка 7 марок.
Більше на 2 – це стільки ж та ще 2. Щоб знайти відповідь на питання, треба виконати дію додавання.
б) Задача на збільшення на кілька одиниць, непряма форма
У Михайлика було 5 марок, це на 2 марки менше, ніж у Сергійка. Скільки марок було у Сергійка?
М. – 5 м., на 2 м. менше
С. – ?
5 + 2 = 7 (м.)
Відповідь: у Сергійка 7 марок.
Якщо у Михайлика на 2 марки менше, ніж у Сергійка, то у Сергійка на 2 марки більше, ніж у Михайлика. Щоб знайти кількість Сергійкових марок, треба виконати дію додавання.
в) Задача на зменшення на кілька одиниць, пряма форма
У Михайлика було 5 марок, а у Сергійка на 2 марки менше. Скільки марок було у Сергійка?
М. – 5 м.
С. – ?, на 2 м. менше
5 – 2 = 3 (м.).
Відповідь: у Сергійка 3 марки.
Менше на 2 означає, що до того, щоб було порівну, не вистачає двох, тобто, це стільки ж але без двох. Отже, щоб знайти скільки марок у Сергійка, треба виконати дію віднімання.
г) Задача на зменшення на кілька одиниць, непряма форма
У Михайлика було 5 марок, це на 2 марки більше, ніж у Сергійка. Скільки марок було у Сергійка?
М. – 5 м., на 2 м. більше
С. – ?
5 – 2 = 3 (м.)
Відповідь: у Сергійка 3 марки.
Якщо у Михайлика на 2 марки більше, ніж у Сергійка, то у Сергійка на 2 марки менше. Щоб дізнатися скільки марок у Сергійка, треба виконати дію віднімання.
д) Задача на різницеве порівняння із словом «більше»
У Михайлика було 5 марок, а у Сергійка 3. На скільки марок більше було у Михайлика, ніж у Сергійка?
5 – 3 = 2 (м.).
Відповідь: на 2 марки більше.
е) Задача на різницеве порівняння із словом «менше»
У Михайлика було 5 марок, а у Сергійка 3. На скільки марок менше було у Сергійка, ніж у Михайлика?
5 – 3 = 2 (м.).
Відповідь: на 2 марки менше.
Щоб дізнатися на скільки одне число менше від другого або більше від другого, від більшого числа віднімаємо менше.
є) Задача на збільшення у кілька разів, пряма форма
У ящику 8 кг цукру, а у мішку – в 9 разів більше. Скільки кілограмів цукру у мішку?
Ящик – 8 кг
Мішок - ?, у 9 разів більше
8 · 9 = 72 (кг).
Відповідь: у мішку 72 кг цукру.
Більше у 9 разів означає що це 9 раз по 8 кг. Щоб знайти скільки це буде, треба виконати дію множення.
ж) Задача на збільшення у кілька разів, непряма форма
У ящику 8 кг цукру, що у 9 разів менше, ніж у мішку. Скільки кілограмів цукру у мішку?
Ящик – 8 кг, у 9 разів менше
Мішок – ?
8 · 9 = 72 (кг).
Відповідь: у мішку 72 кг цукру.
Якщо у ящику у 9 разів цукру менше, ніж у мішку, то у мішку його у 9 разів більше. Щоб дізнатися скільки цукру у мішку, треба виконати дію множення.
з) Задача на зменшення у кілька разів, пряма форма
У спортивний табір прибуло 24 футболісти, а волейболістів – у 3 рази менше. Скільки волейболістів прибуло у спортивний табір?
Ф. – 24
В. – ?, у 3 рази менше
24 : 3 = 8 (в.).
Відповідь: 8 волейболістів
У 3 рази менше означає, що число волейболістів 3 рази вміщується у числі футболістів. Щоб дізнатись кількість волейболістів, треба кількість футболістів поділити на 3.
и) Задача на зменшення у кілька разів, непряма форма
У спортивний табір прибуло 24 футболісти, що у 3 рази більше, ніж волейболістів. Скільки волейболістів прибуло у спортивний табір?
Ф. – 24, у 3 рази більше
В. – ?
24 : 3 = 8 (в.).
Відповідь: 8 волейболістів
Якщо футболістів у 3 рази більше, ніж волейболістів, то волейболістів у 3 рази менше. Щоб дізнатись кількість волейболістів, треба виконати дію ділення.
і) Задача на кратне порівняння із словом «більше»
Для приготування клею взяли 2 склянки крохмалю і 18 склянок води. У скільки разів більше взяли води, ніж крохмалю?
18 : 2 = 9 (р.).
Відповідь: у 2 рази більше.
ї) Задача на кратне порівняння із словом «менше»
Для приготування клею взяли 2 склянки крохмалю і 18 склянок води. У скільки разів менше взяли крохмалю, ніж води?
18 : 2 = 9 (р.).
Відповідь: у 9 разів менше.
Щоб дізнатися у скільки разів одне число менше чи більше за друге, більше число ділимо на менше.
Учні часто плутають поняття «більше на …» і «більше у …», «менше на …» і «менше у …». Тому корисним є розв’язування пар подібних задач і їх порівняння.
а) У чайнику 3 л води, а у каструлі на 2 л більше. Скільки води у каструлі?
б) У чайнику 3 л води, а у каструлі у 2 рази більше. Скільки води у каструлі?
Результати порівняння:
Задачі про одне і те ж. Числові дані однакові. Але у першій задачі відношення «на … більше», тому задача розв’язується дією додавання. У другій задачі відношення «у … більше», тому задача розв’язується дією множення. Виконання різних дій дає різну відповідь до задач.
В) Задачі на знаходження невідомих компонентів дій
а) Задача на знаходження невідомого доданка
На урок фізкультури принесли 10 м’ячів: із них – 6 великих, а решту малі. Скільки малих м’ячів принесли на урок фізкультури?
В
еликих
– 6 м.
Малих – ? 10 м.
10 – 6 = 4 (м.).
Відповідь: 4 малих м’ячі.
б) Задача на знаходження невідомого зменшуваного
У дворі гралися діти. Коли троє із них пішли додому, то у дворі залишилося ще п’ятеро. Скільки дітей було у дворі спочатку?
Було - ?
Пішли – 3 д.
Залишилося – 5 д.
3 + 5 = 8 (д.).
Відповідь: спочатку було 8 дітей.
в) Задача на знаходження невідомого від’ємника
На годівниці сиділо 10 пташок. Коли кілька пташок відлетіло, то там залишилося ще 6. Скільки пташок відлетіло?
Сиділо – 10 п.
Відлетіло – ? п.
Залишилося – 6 п.
10 – 6 = 4 (п.).
Відповідь: відлетіло 4 пташки.
Задачі на знаходження невідомих компонентів дій додавання і віднімання розв’язуються, як правило, арифметичним способом. Шлях до розв’язання підказує короткий запис задачі з використанням відповідних символів чи опорних слів. У третьому-четвертому класах автори підручника рекомендують розв’язувати деякі такі задачі алгебраїчним способом.
Задачі на знаходження невідомих компонентів дій множення і ділення у підручнику подаються абстрактні, розв’язуються вони, як правило, алгебраїчним способом. За текстом складають і розв’язують рівняння.
г) Задача на знаходження невідомого множника
Якщо задумане число помножити на 3, то одержимо 18. Яке число задумали?
д) Задача на знаходження невідомого діленого
Невідоме число зменшили у 3 рази і дістали 9. Знайди невідоме число.
е) Задача на знаходження невідомого дільника
На яке число треба поділити 42, щоб одержати 7? Склади рівняння і розв’яжи його.
Крім цих простих задач, основне призначення яких розкривати випадки застосування арифметичних дій, у початковому курсі розглядають ще прості сюжетні задачі, які розкривають зв'язок між трьома взаємо пов’язаними величинами: швидкість, час, відстань; ціна, кількість, вартість та ін., а також на обчислення площі прямокутника та задачі на знаходження частини від числа і числа за його частиною. Проте абстрагуючись від величин, ту чи іншу задачу із вказаних можна віднести до одного із розглянутих вище видів. Наприклад, задачу на знаходження числа за його частиною можна інтерпретувати як задачу на знаходження невідомого діленого.
Ознайомлення із оберненою задачею
1клас
Поняття про обернену задачу вводиться на прикладі задачі на знаходження суми
Самовар вміщує 5 л води, а банка 3 л. Скільки літрів води вміщують разом самовар і банка?
5 + 3 = 8 (л).
Відповідь: У самоварі і банці разом 8 літрів води.
Самовар і банка вміщують разом 8 л води. Самовар вміщує 5 л води. Скільки літрів води вміщує банка?
8 – 5 = 3 (л).
Відповідь: банка вміщує 3 л води.
С п і л ь н е: Один і той же сюжет (одна і таж ситуація); частина чисел співпадає;
В і д м і н н е: Те що запитувалось у першій задачі, стало відомим у другій задачі, а одне з чисел, що було відомим у першій задач, стало невідомим; різними діями знаходиться розв’язання задачі; різні відповіді, але відповідь другої задачі співпадає з числом, даним у першій задачі.
Друга задача є оберненою до першої, а перша є оберненою до другої, обидві задачі разом називаються взаємно оберненими. До кожної з цих задач можна скласти ще одну обернену задачу, в якій буде знаходитись кількість води, що вміщує самовар. В загальному: до кожної задачі можна скласти стільки обернених задач, скільки чисел вказується у даній.
Лекція 3. Методика навчання учнів розв’язування складених задач