13.3. Сила Лоренца

• Сила Лоренца действует со стороны магнитного поля на движущийся заряд. Воспользуемся выражением силы Ампера:

; — скорость частицы, — заряд частицы, — сила Лоренца, поэтому

.

• Д 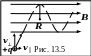вижение заряженной частицы в магнитном поле

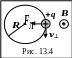
Сила Лоренца пропорциональна векторному произведению скорости частицы и вектора индукции, поэтому она всегда перпендикулярна скорости, то есть является центростремительной силой. Сила Лоренца не совершает механической работы, частицы движутся в однородном поле по круговой траектории (рис. 13.4) или по спирали (рис. 13.5).

На первом рисунке положительно заряженная частица массой m со скоростью движется перпендикулярно индукции магнитного поля B. Определим радиус кривизны ее траектории R. По второму закону Ньютона

.

13.4. Закон Био-Савара-Лапласа

• З 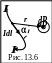акон Био-Савара-Лапласа определяет магнитную индукцию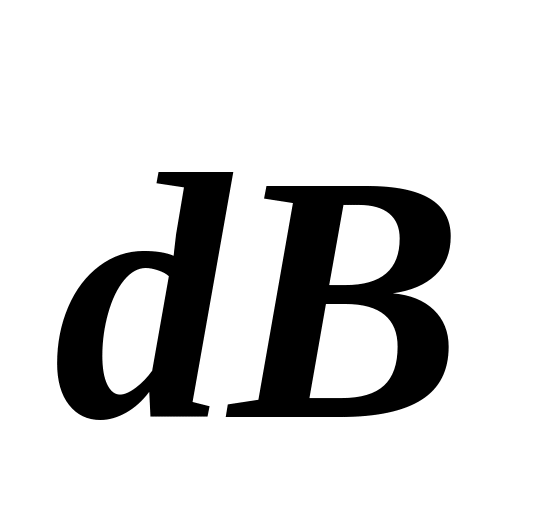 , создаваемую элементом тока в заданной точке (рис. 13.6):

.

Здесь ₀ — магнитная постоянная, ₀ = 4πּ10^–7 Ф/м. Для определения магнитной индукции, создаваемой конечным током, используется принцип суперпозиции: , где L — контур проводника с током.

— магнитная проницаемость среды показывает во сколько раз магнитная индукция поля в среде B отличается от индукции в вакууме B₀:

.

• Напряженность магнитного поля , А/м — вспомогательная силовая характеристика магнитного поля, не зависящая от магнитных свойств среды:

• Закон Био-Савара-Лапласа для напряженности магнитного поля:

.

• Н апряженность и индукция поля в центре и на оси кругового тока

Рассмотрим круговой контур радиуса R с током I (рис. 13.7).

Используя принцип суперпозиции и закон Био –Савара –Лапласа для напряженности магнитного поля, получаем в центре витка:

.

Таким образом,

, .

Если исследуемая точка находится на оси витка, то

, .

Эта формула подобна напряженности поля электрического диполя (11.3).

• Н 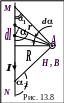апряженность и индукция магнитного поля прямого тока

По закону Био—Савара—Лапласа напряженность , создаваемая элементом тока в точке А равна (рис. 13.8):

_.

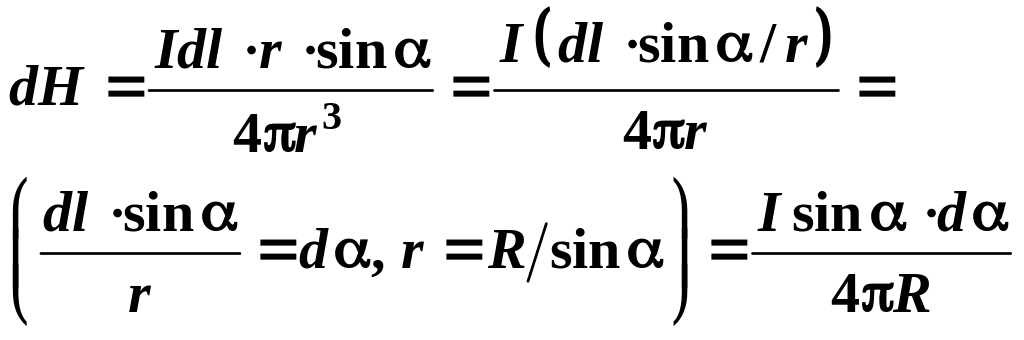Векторы всех малых элементов провода MN направлены в точке наблюдения поля А одинаково — из-за чертежа перпендикулярно его плоскости, поэтому

.

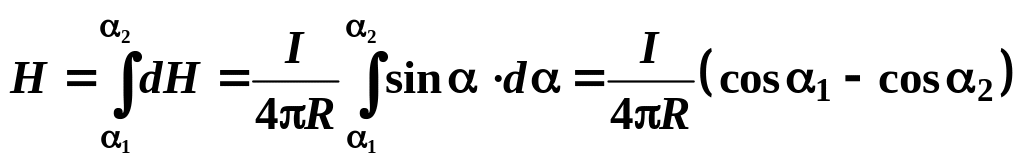Для бесконечного провода , где — расстояние от тока до точки наблюдения поля .

13.5. Теорема Остроградского – Гаусса для магнитного поля

Линии магнитной индукции — в каждой точке этих линий вектор магнитной индукции направлен по касательной. Линии магнитной индукции замкнуты (нет магнитных зарядов). Их направление связано с направлением тока правилом правого буравчика. Такие поля называются вихревыми. Индукция магнитного поля вне тела магнитов направлена от северного полюса к южному.

• П римеры линий индукции для магнита и разных токов:

Поле внутри соленоида (рис. 13.12) однородно, то есть

.

• П оток магнитной индукции, Ф_B, Вб (Вебер)

Потоком Ф_B вектора магнитной индукции через поверхность площадью S называется число линий индукции, пересекающих заданную поверхность. Элемент потока dФ_B через элемент поверхности dS определяется формулой (рис. 13.13) . — угол между единичным вектором нормали к поверхности контура и вектором индукции . Введем обозначение , тогда . Конечный поток через поверхность S:

.

• Т еорема Остроградского - Гаусса для магнитного поля

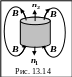
Поток магнитной индукции через любую замкнутую поверхность, равен нулю:

Рассуждения.

Поместим замкнутую поверхность в магнитное поле (рис. 13.14). Линии магнитной индукции замкнуты, поэтому входящий поток индукции (-2 Вб) равен выходящему (+2 Вб). Суммарный поток магнитной индукции через любую замкнутую поверхность равен нулю.