
- •Глава 11
- •11.2. Закон Кулона
- •1Электрическое поле. Напряженность и индукция поля
- •11.4. Теорема Остроградского – Гаусса
- •11.5. Работа электростатического поля. Разность потенциалов. Потенциал
- •11.6. Эквипотенциальные поверхности
- •1 1.7. Связь напряженности и потенциала
- •11.8. Диэлектрики в электростатическом поле
- •11.9. Проводники в электростатическом поле
- •11.10. Электроемкость проводников
- •11.11. Электроемкость конденсаторов
- •11.12. Соединения конденсаторов
- •11.13. Энергия электрического поля
- •Глава 12 постоянный электрический ток
- •12.1. Основные понятия и определения
- •12.2. Закон Ома для однородного участка цепи. Сопротивление проводников
- •12.3. Вывод дифференциального закона Ома (для металлов)
- •12.4. Электродвижущая сила
- •12.5. Интегральный закон Ома для участка цепи, содержащего источник тока
- •1 2.6. Интегральный закон Ома для замкнутой (полной) цепи
- •12.7. Разветвленные цепи. Правила Кирхгофа
- •12.8. Работа и мощность постоянного тока. Кпд
- •Глава 13 электромагнетизм
- •13.1. Магнитное поле
- •13.2. Закон Ампера
- •13.3. Сила Лоренца
- •13.4. Закон Био-Савара-Лапласа
- •13.5. Теорема Остроградского – Гаусса для магнитного поля
- •13.6. Закон полного тока. (Теорема о циркуляции)
- •13.7. Поле, движущегося заряда
- •13.8. Механическая работа контура с током в магнитном поле
- •Глава 14 электромагнитная индукция
- •14.1.Основной закон электромагнитной индукции
- •14.2. Вихревое электрическое поле
- •14.3. Самоиндукция
- •14.4. Взаимная индукция
- •14.5. Э нергия магнитного поля
- •Глава 15 магнитное поле в веществе
- •15.1. Магнетики
- •15.2. Парамагнетики
- •15.3. Диамагнетики
- •15.4. Ферромагнетики
- •Глава 16 электромагнитные колебания
- •16.1. Свободные электромагнитные колебания
- •16.2. Период и частота свободных колебаний
- •16.3. Свободные затухающие колебания
- •16.4. Вынужденные колебания
- •16.5. Работа и мощность в цепи переменного тока
- •Глава 17 электромагнитное поле
- •17.1. Первая пара уравнений Максвелла. Ток смещения
- •17.2. Вторая пара уравнений Максвелла
- •17.3. Электромагнитные волны
- •17.4. Свойства электромагнитных волн
11.5. Работа электростатического поля. Разность потенциалов. Потенциал
Раб
 ота
электростатического поля при перемещении
заряда не зависит от траектории
движения заряда, а определяется только
начальной и конечной точками перемещения.
ота
электростатического поля при перемещении
заряда не зависит от траектории
движения заряда, а определяется только
начальной и конечной точками перемещения.
Доказательство.
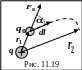
Определим работу А12 , которую совершает поле точечного заряда q при перемещении заряда q0 из точки r1 в точку r2 (рис. 11.19). По определению механической работы:
Циркуляция напряженности электростатического поля U, В -это работа по перемещению единичного положительного заряда по замкнутому контуру L. В электростатическом поле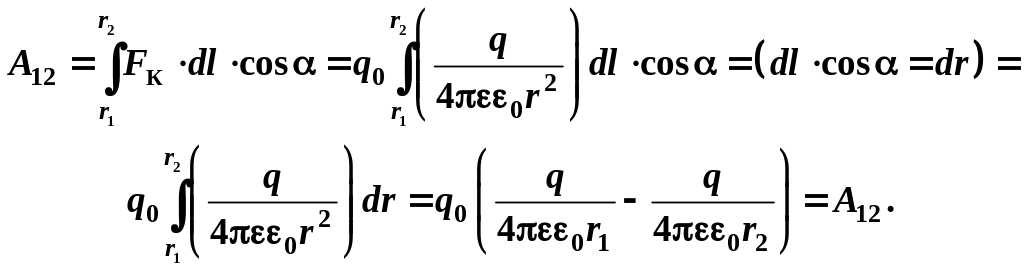
![]() .
.
Независимость работы поля от траектории движения заряда позволяет ввести понятие разности потенциалов или напряжения.
Разность потенциалов , В (вольт) или напряжение U между точками 1 и 2 — это работа, которую могут совершить силы электрического поля при перемещении единичного положительного заряда из т.1 в т.2.
![]()
Работа поля при перемещении заряда q:
A12
= q ( =q
U.
q ( =q
U.
Работа, совершаемая силами электрического поля при перемещении заряда, приводит к уменьшению потенциальной энергии заряда в поле
A12 = – WП .
Потенциал точки поля , В — это работа, которую могут совершить силы электрического поля при перемещении единичного положительного заряда из данной точки в бесконечность (максимальная работа). Потенциал численно равен потенциальной энергии единичного положительного заряда в этой точке.
![]() WП
= q .
WП
= q .
Потенциал поля точечного заряда q на расстоянии r от него:
![]()
Принцип суперпозиции для потенциалов. Потенциал электрического поля системы зарядов равен алгебраической сумме потенциалов полей, создаваемых каждым зарядом:
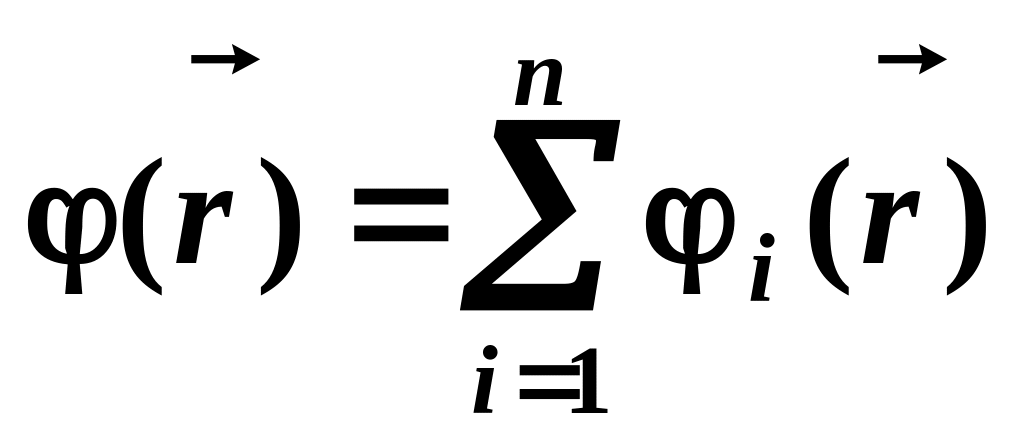 .
.
11.6. Эквипотенциальные поверхности
Э
 квипотенциальные
поверхности — это геометрическое
место точек, имеющих одинаковый
потенциал. Например, эквипотенциальные
поверхности точечного заряда (или шара)
являются сферическими поверхностями
(рис. 11.20),
квипотенциальные
поверхности — это геометрическое
место точек, имеющих одинаковый
потенциал. Например, эквипотенциальные
поверхности точечного заряда (или шара)
являются сферическими поверхностями
(рис. 11.20),
![]() .
.
При
перемещении заряда по эквипотенциальной
поверхности работа не совершается:
![]() .
Для этого угол α должен быть равен
90º. Поэтому
силовые линии перпендикулярны
эквипотенциальным поверхностям.
.
Для этого угол α должен быть равен
90º. Поэтому
силовые линии перпендикулярны
эквипотенциальным поверхностям.
1 1.7. Связь напряженности и потенциала
Определим работу по перемещению заряда q0 вдоль силовой
линии на расстояние dl (рис. 11.21):
![]()
![]()
С
другой стороны:
![]() .
Сравнивая, получаем:
.
Сравнивая, получаем:
![]() .
.
Для
однородного поля, например, поля плоского
конденсатора,
![]() ,
где U и
d — напряжение
и расстояние между обкладками. Таким
образом, напряженность равна скорости
изменения потенциала в пространстве.
Скорость изменения скалярной величины
в пространстве называется градиентом
этой величины:
,
где U и
d — напряжение
и расстояние между обкладками. Таким
образом, напряженность равна скорости
изменения потенциала в пространстве.
Скорость изменения скалярной величины
в пространстве называется градиентом
этой величины:
![]()
11.8. Диэлектрики в электростатическом поле
Диэлектрики. В электрическом отношении все вещества делятся на проводники, полупроводники и диэлектрики. Диэлектрики (изоляторы) практически не проводят электрический ток (стекло, пластмассы, фарфор, сухое дерево, масла, чистая вода, газы). Диэлектрики построены из молекул (атомов) с равным кол
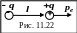 ичеством
положительных и отрицательных зарядов
(рис. 11.22). Они не могут перемещаться под
действием электрического поля и образуют
электрические диполи. Напомним, что
— электрический дипольный момент —
векторная характеристика диполя.
ичеством
положительных и отрицательных зарядов
(рис. 11.22). Они не могут перемещаться под
действием электрического поля и образуют
электрические диполи. Напомним, что
— электрический дипольный момент —
векторная характеристика диполя.
Д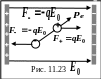
 иполь
в электрическом поле. Во внешнем
электрическом поле на диполь действует
пара сил
иполь
в электрическом поле. Во внешнем
электрическом поле на диполь действует
пара сил
![]() и
и
![]() (рис. 11.23), ориентирующих дипольный момент
(рис. 11.23), ориентирующих дипольный момент
![]() по напряженности внешнего поля.
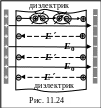
За счет этого, на гранях диэлектрика
возникают нескомпенсированные
поляризационные заряды (рис. 11.24),
которые своим полем с напряженностью
по напряженности внешнего поля.
За счет этого, на гранях диэлектрика
возникают нескомпенсированные
поляризационные заряды (рис. 11.24),
которые своим полем с напряженностью
![]() уменьшают напряженность внешнего поля
уменьшают напряженность внешнего поля
![]() .
Этот процесс называется поляризацией
диэлектрика. Результирующая напряженность
.
Этот процесс называется поляризацией
диэлектрика. Результирующая напряженность
![]() .
Диэлектрики ослабляют электрическое
поле.
.
Диэлектрики ослабляют электрическое
поле.
Типы диэлектриков. По способу возникновения поляризационных зарядов диэлектрики делятся на три типа.
Н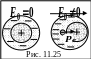 еполярные
диэлектрики состоят из неполярных
молекул, у которых "центры тяжести"
положительных и отрицательных зарядов
совпадают (N2, O2,
H2, CCl4).
Во внешнем электрическом поле возникает
деформация электронных оболочек атомов
и молекул (рис. 11.25). За счет этого у
молекул возникает индуцированный
(наведенный) дипольный момент
еполярные
диэлектрики состоят из неполярных
молекул, у которых "центры тяжести"
положительных и отрицательных зарядов
совпадают (N2, O2,
H2, CCl4).
Во внешнем электрическом поле возникает
деформация электронных оболочек атомов
и молекул (рис. 11.25). За счет этого у
молекул возникает индуцированный
(наведенный) дипольный момент
![]() ,
пропорциональный напряженности поля
.
Это явление называется электронной
поляризацией.
,
пропорциональный напряженности поля
.
Это явление называется электронной
поляризацией.
При
отсутствии внешнего поля поляризация
отсутствует. П олярные
диэлектрики состоят из молекул, у
которых "центры тяжести" положительных
и отрицательных зарядов не совпадают
даже в отсутствии внешнего поля, образуя
жесткие диполи (спирты, H2O,
некоторые пластмассы).
олярные
диэлектрики состоят из молекул, у
которых "центры тяжести" положительных
и отрицательных зарядов не совпадают
даже в отсутствии внешнего поля, образуя
жесткие диполи (спирты, H2O,
некоторые пластмассы).
При тепловом движении в отсутствии внешнего поля диполи ориентированы хаотически. Поэтому их суммарный (объемный) дипольный момент равен нулю — поляризации нет (рис. 11.26,а). При включенном внешнем электрическом поле дипольные моменты колеблются вблизи направления внешнего поля. Суммарный дипольный мо5мент отличен от нуля— поляризация есть (рис. 11.26,б). Это явление называется ориентационной поляризацией.
И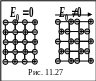 онная
поляризация происходит в твердых
диэлектриках, имеющих ионную кристаллическую
решетку. Внешнее электрическое поле
вызывает в таких диэлектриках смещение
(рис. 11.27) всех положительных ионов в
направлении напряженности поля, а всех
отрицательных ионов в противоположную
сторону. За счет этого происходит
незначительное изменение объема
кристалла. Это явление называется
электрострикцией.
онная
поляризация происходит в твердых
диэлектриках, имеющих ионную кристаллическую
решетку. Внешнее электрическое поле
вызывает в таких диэлектриках смещение
(рис. 11.27) всех положительных ионов в
направлении напряженности поля, а всех
отрицательных ионов в противоположную
сторону. За счет этого происходит
незначительное изменение объема
кристалла. Это явление называется
электрострикцией.
Электрическое поле в диэлектрике
Вектор
поляризации (поляризованность)
— дипольный момент единицы объема
диэлектрика:
![]() ,
где
,
где
![]() — дипольный момент
— дипольный момент
![]() –ой
молекулы,
–ой
молекулы,
![]() — число молекул в малом объеме
— число молекул в малом объеме
![]() .
.
Поле
в малом объеме неполярного диэлектрика
можно считать однородным, тогда все
молекулы неполярного диэлектрика
приобретут одинаковый дипольный момент
,
поэтому поляризованность неполярного
диэлектрика в электрическом поле
напряженностью
равна:
![]() ,
где
,
где
![]() — концентрация молекул. Используя
,
получаем
— концентрация молекул. Используя
,
получаем
![]() ,
где
,
где
![]() — безразмерная
величина — диэлектрическая восприимчивость
неполярного диэлектрика, не зависисящая
от температуры.
— безразмерная
величина — диэлектрическая восприимчивость
неполярного диэлектрика, не зависисящая
от температуры.
Для полярного диэлектрика поляризованность
![]() ,
,
где
![]() — среднее значение дипольного момента
молекулы.
— среднее значение дипольного момента
молекулы.
Можно
показать (Дебай — Ланжевен), что в слабых
электрических полях
![]() ,
следовательно
,
следовательно
![]() — диэлектрическая восприимчивость
полярного диэлектрика. Чем больше
температура (тепловое движение), тем
слабее диполи ориентируются во внешнем
поле.
— диэлектрическая восприимчивость
полярного диэлектрика. Чем больше
температура (тепловое движение), тем
слабее диполи ориентируются во внешнем
поле.
П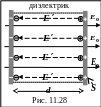 оле,
создаваемое поляризационными зарядами
(рис. 11.28), можно рассчитать как поле
плоского конденсатора с поверхностной
плотностью заряда
оле,
создаваемое поляризационными зарядами
(рис. 11.28), можно рассчитать как поле
плоского конденсатора с поверхностной
плотностью заряда
![]() :
:
![]() .
Дипольный момент всего объема диэлектрика
.
Дипольный момент всего объема диэлектрика
![]() ,
где
,
где
![]() — площадь боковой грани диэлектрика.
С другой стороны, поляризованный
диэлектрик можно рассматривать как
диполь с плечом
— площадь боковой грани диэлектрика.
С другой стороны, поляризованный
диэлектрик можно рассматривать как
диполь с плечом
![]() и зарядом
и зарядом
![]() .
По определению дипольного момента
.
По определению дипольного момента
![]() .
Сравнивая, получаем
.
Сравнивая, получаем
![]() ,
тогда
,
тогда
![]() .
.
![]()
Напряженность поля, создаваемого поляризационными зарядами, пропорциональна поляризованности.
Электрическое поле внутри диэлектрика
Обратимся
к ранее рассмотренной ситуации плоского
конденсатора, заполненного диэлектриком
(рис 28). По принципу суперпозиции
напряженность поля внутри диэлектрика
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]()
![]()
![]() .
Сравнивая с определением
диэлектрической проницаемости
.
Сравнивая с определением
диэлектрической проницаемости
![]() ,
получаем:
,
получаем:
![]() .
.
Чем больше диэлектрическая восприимчивость, тем легче деформируются (ориентируются) молекулы, тем сильнее происходит уменьшение внешнего поля.
Вектор
индукции
![]()
![]()
![]() .
.
Это
наиболее общая связь вектора
электростатической индукции и
напряженности поля в диэлектрике. Она
не зависит от формы закона
![]() .
.
 Условия
для электрического поля на границе
раздела двух диэлектриков
Условия
для электрического поля на границе
раздела двух диэлектриков
На
границе двух диэлектриков векторы
и
![]() можно представить в виде
можно представить в виде
![]() ,
аналогично
,
аналогично
![]() ,
где
,
где
![]() — тангенциальный (касательный к границе
раздела),
— нормальный (перпендикулярный к границе
раздела) единичные векторы (рис.
11.29,11.30).
— тангенциальный (касательный к границе
раздела),
— нормальный (перпендикулярный к границе
раздела) единичные векторы (рис.
11.29,11.30).
Величина
нормальной составляющей напряженности
![]() испытывает скачек
испытывает скачек
![]() ,
а тангенциальная составляющая не
меняется
,
а тангенциальная составляющая не
меняется
![]() .
Поэтому линии напряженности на границе
двух диэлектриков
.
Поэтому линии напряженности на границе
двух диэлектриков 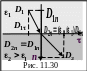 преломляются
(рис. 11.29), поток вектора напряженности
преломляются
(рис. 11.29), поток вектора напряженности
![]() скачком меняет свое значение.
скачком меняет свое значение.
Наоборот,
величина тангенциальной составляющая
вектора электростатической индукции
![]() испытывает скачек
испытывает скачек
![]() ,
а нормальная составляющая
,
а нормальная составляющая
![]() не меняется. Линии индукции на границе
двух диэлектриков тоже преломляются
(рис. 30), но поток вектора индукции
не меняется. Линии индукции на границе
двух диэлектриков тоже преломляются
(рис. 30), но поток вектора индукции
![]() остается постоянным, что позволяет
сформулировать теорему Гаусса–Остроградского
в удобном виде
остается постоянным, что позволяет
сформулировать теорему Гаусса–Остроградского
в удобном виде
![]() .
.
Сегнетоэлектриками называется группа кристаллических диэлектриков, обладающих самопроизвольной (спонтанной) поляризацией, которая сильно изменяется под влиянием внешнего поля, деформации, изменения температуры (сегнетова соль — NaKC4H4O6ּ4H20; BaTiO3). Свойства сегнетоэлектриков подобны свойствам ферромагнетиков.
В отсутствии
внешнего электрического поля весь объем
сегнетоэлектрика разбит на небольшие
области, которые поляризованы до
насыщения и называются доменами.
При включении внешнего электрического
поля, происходит рост доменов, векторы
электрических моментов которых близки
по направлению к напряженности
внешнего поля, при дальнейшем увеличении
происходит поворот электрических
моментов по полю. При достаточно больших
наступает насыщение и поляризованность
![]() не меняется с ростом
.
Диэлектрическая проницаемость
сегнетоэлектриков достигает очень
больших значений
не меняется с ростом
.
Диэлектрическая проницаемость
сегнетоэлектриков достигает очень
больших значений
![]() .
.
