16.5. Работа и мощность в цепи переменного тока
В
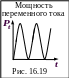ыделение
мощности на активном сопротивлении
Сила тока и напряжение на активном сопротивлении меняются синфазно (16.4.), поэтому мощность, выделяемая на активном сопротивлении (рис. 16.19):
.
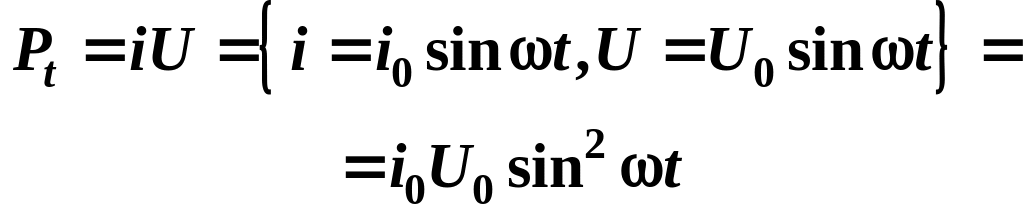Работа переменного тока за один период
Из определения мощности
.
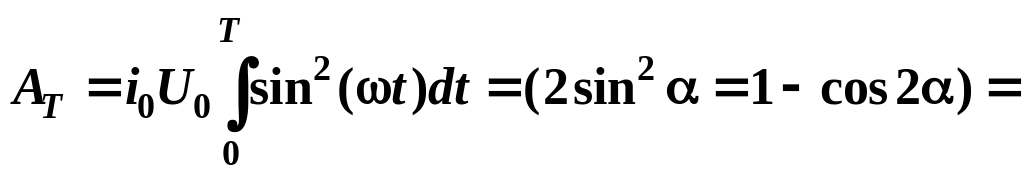
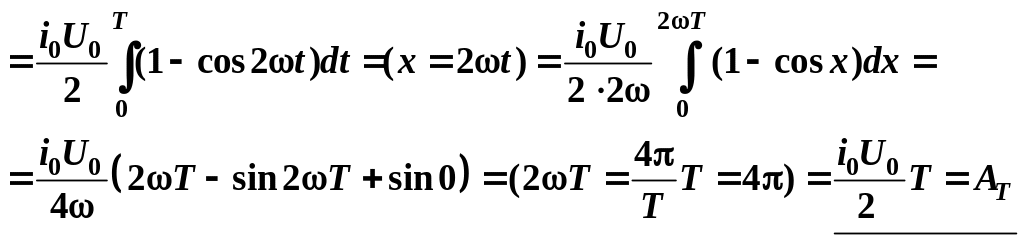
Средняя мощность
,
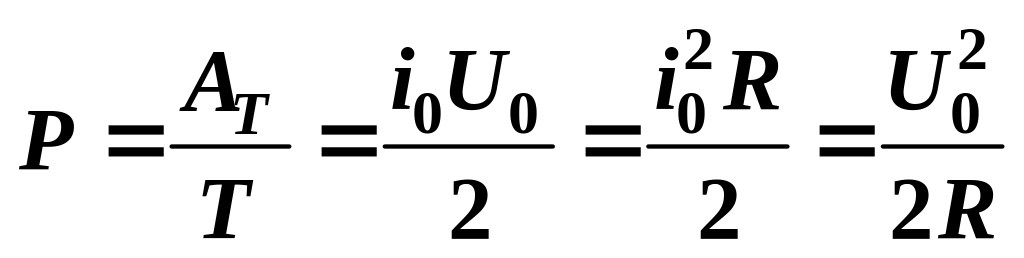где
— амплитудные значения тока и напряжения.
Эффективные значения переменного тока и напряжения
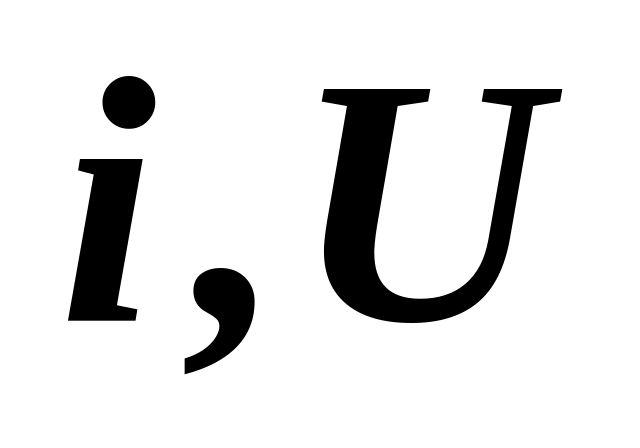— это их значения для постоянного тока
такой же мощности:
Коэффициент мощности
.
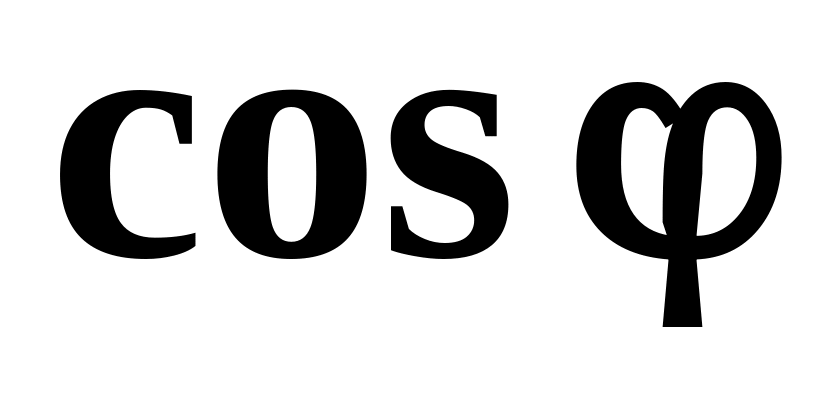С использованием эффективных значений переменного тока и напряжения формуле средней мощности можно придать вид:
.
Если
реактивное сопротивление
равно нулю (резонанс), то (согласно 16.4)
— выделяется максимальная мощность.
На реактивных сопротивлениях мощность
не выделяется.
Глава 17 электромагнитное поле
Система из четырех уравнений Максвелла полностью описывает электромагнитные процессы.
17.1. Первая пара уравнений Максвелла. Ток смещения
П
ервое
уравнение Максвелла было нами
получено в 14.2. Оно связывает
переменное магнитное и вихревое
электрическое поля:
Скорость изменения магнитного потока равна циркуляции напряженности вихревого электрического поля.
Другими словами, переменное магнитное поле порождает вихревое электрическое поле (рис. 17.1). Но должно быть и обратное: переменное электрическое поле способно порождать вихревое магнитное поле. Докажем это.
Ток смещения
— физическая величина, описывающая
переменное электрическое поле в
диэлектриках. Для переменного тока
диэлектрический зазор конденсатора
не является непреодолимым препятствием
(16.4). В цепи переменного тока плотность
заряда
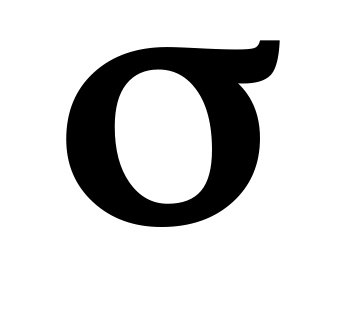на обкладках конденсатора меняется,
что можно интерпретировать как некий
ток, текущий через диэлектрик. Этот
якобы ток и называется током смещения
.
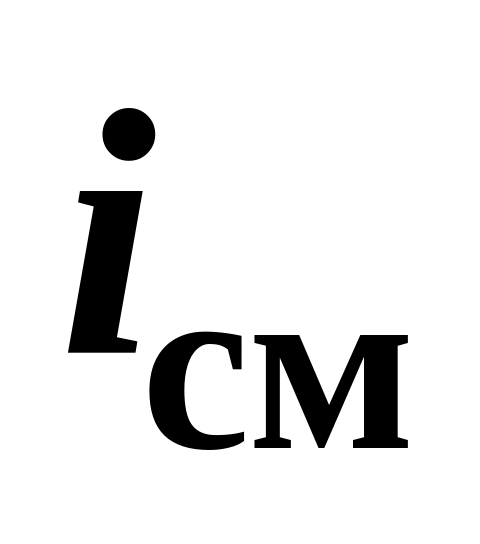Максвелл доказал, что этот ток создает
магнитное поле, как и обычный ток
проводимости. На самом деле, в диэлектрике
конденсатора существует переменное
электрическое поле, которое и порождает
магнитное поле. Свяжем силу тока смещения
с индукцией переменного электрического
поля.
{
;
— площадь обкладки}=
.
Сила тока смещения равна скорости изменения потока вектора электрической индукции внутри конденсатора.
Второе
уравнение Максвелла
получается из теоремы о циркуляции
напряженности магнитного поля (13.6):
.
Для
вакуума
=
0, поэтому
.
С
корость
изменения потока электрической индукции
равна циркуляции напряженности магнитного
поля. Другими словами, переменное
электрическое поле порождает вихревое
магнитное поле (рис. 17.2).
17.2. Вторая пара уравнений Максвелла
– это теоремы Остроградского - Гаусса о существовании зарядов.
Третье уравнение Максвелла (теорема Остроградского - Гаусса для электрического поля, см. 11.4)
Поток вектора электрической индукции через любую замкнутую поверхность, охватывающую систему зарядов, равен алгебраической сумме зарядов внутри поверхности:
.
Четвертое уравнение Максвелла (теорема Остроградского - Гаусса для магнитного поля, см. 13.5)
Поток магнитной индукции через любую замкнутую поверхность равен нулю (то есть, магнитные заряды не существуют):
.
К этим четырем уравнениям следует добавить соотношения, учитывающие электрические и магнитные свойства сред:
— связь индукции
и напряженности электрического поля,
— связь индукции
и напряженности магнитного поля,
— связь плотности
тока и напряженности электрического
поля (дифференциальный закон Ома).
Эти четыре уравнения и связи описывают все электромагнитные явления, происходящие в покоящихся средах.