15.3 Удвоение длины блока

В академическом сообществе давно спорят на тему, достаточна ли 64-битовая длина блока. С одной стороны 64-битовый блок обеспечивает диффузию открытого текста только в 8 байтах шифротекста. С другой стороны более длинный блок затрудняет безопасную маскировку структуры, кроме того, больше возможностей ошибиться.

Существуют предложения удваивать длину блока алгоритма с помощью многократного шифрования [299]. Прежде, чем реализовывать одно из них, оцените возможность вскрытия "встреча посередине". Схема Ричарда Аутбриджа (Richard Outerbridge) [300], показанная на 12-й, не более безопасна, чем тройное шифрование с оди­нарным блоком и двумя ключами [859].

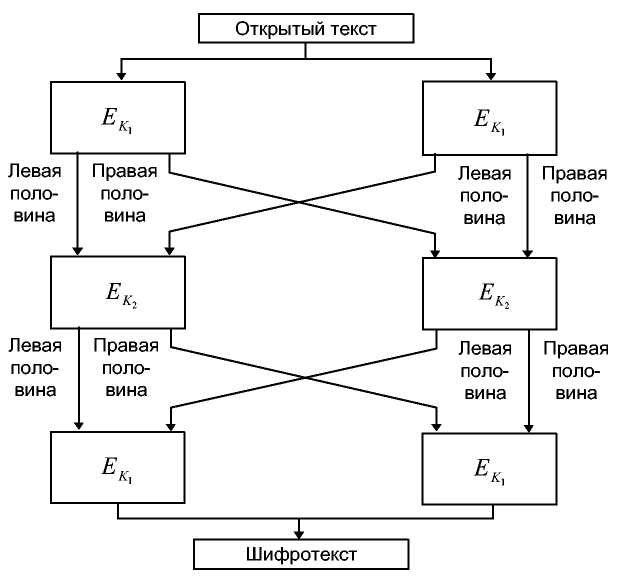
Рис. 15-3. Удвоение длины блока.

Однако я не рекомендую использовать подобный прием. Он не быстрее обычного тройного шифрования: для шифрования двух блоков данных все также нужно шесть шифрований. Характеристики обычного тройного шифрования известны, а за новыми конструкциями часто прячутся новые проблемы.

15.4 Другие схемы многократного шифрования

Проблемой тройного шифрования с двумя ключами является то, что для увеличения вдвое пространства ключей нужно выполнять три шифрования каждого блока открытого текста. Разве не здорово было бы найти какой-нибудь хитрый способ объединить два шифрования, которые удвоили бы пространство ключей?

Двойной OFB/счетчик

Этот метод использует блочный алгоритм для генерации двух потоков ключей, которые используются для шифрования открытого текста.

S_i=E_K1 (S_i-1I₁);I₁=I₁+1

T_i=E_K2 (T_i-1I₂);I₂=I₂+1

C₁=P_iS_iT_i

S_i и T_i - внутренние переменные, а I₁ и I₂ - счетчики. Две копии блочного алгоритма работают в некотором гибридном режиме OFB/счетчик, а открытый текст, S_i и T_i объединяются с помощью XOR. Ключи К₁ и К₂ независимы. Результаты криптоанализа этого варианта мне неизвестны.

ЕСВ + OFB

Этот метод был разработан для шифрования нескольких сообщений фиксированной длины, например, блоков диска [186, 188]. Используются два ключа: К₁ и К₂. Сначала для генерации маски для блока нужной длины используется выбранный алгоритм и ключ. Эта маска будет использована повторно для шифрования сообщений теми же ключами. Затем выполняется XOR открытого текста сообщения и маски. Наконец результат XOR шиф­руется с помощью выбранного алгоритма и ключа Кг в режиме ЕСВ.

Анализ этого метода проводился только в той работе, в которой он и был опубликован . Понятно, что он не слабее одинарного шифрования ЕСВ и возможно также силен, как и двойное применение алгоритма. Вероятно, криптоаналитик может выполнять поиск ключей независимо, если он получит несколько открытых текстов файлов, зашифрованных одним ключом.

Чтобы затруднить анализ идентичных блоков в одних и тех же местах различных сообщений, можно использовать IV. В отличии от использования IV в других режимах в данном случае перед шифрованием ЕСВ выпол­няется XOR каждого блока сообщения с IV.

Мэтт Блэйз (Matt Blaze) разработал этот режим для своей UNIX Cryptographic File System (CFS, криптогра­фическая файловая система). Это хороший режим, поскольку скрытым состоянием является только одно шифрование в режиме ЕСВ, маска может быть сгенерирована только один раз и сохранена. В CFS в качестве блоч­ного алгоритма используется DES.

xDESⁱ

В [1644, 1645] DES используется как компонент ряда блочных алгоритмов с увеличенными размерами ключей и блоков. Эти схемы никак не зависят от DES, и в них может использоваться любой блочный алгоритм.

Первый, xDESⁱ, представляет собой просто схему Luby-Rackoff с блочным шифром в качестве базовой функции (см. раздел 14.11). Размер блока в два раза больше размера блока используемого блочного фильтра, а размер ключа в три раза больше, чем у используемого блочного фильтра. В каждом из 3 этапов правая половина шифруется блочным алгоритмом и одним из ключей, затем выполняется XOR результата и левой половины, и половины переставляются.

Это быстрее, чем обычное тройное шифрование, так как тремя шифрованиями шифруется блок, длина которого в два раза больше длины блока используемого блочного алгоритма. Но при этом существует простое вскрытие "встреча посередине", которое позволяет найти ключ с помощью таблицы размером 2^k, где k - это размер ключа блочного алгоритма. Правая половина блока открытого текста шифруется с помощью всех возможных значений К₁, выполняется XOR с левой половиной открытого текста и полученные значения сохраня­ются в таблице. Затем правая половина шифротекста шифруется с помощью всех возможных значений К₃, и выполняется поиск совпадений в таблице. При совпадении пара ключей К₁ и К₃ - возможный вариант правого ключа. После нескольких повторений вскрытия останется только один кандидат. Таким образом, xDES¹ не яв­ляется идеальным решением. Даже хуже, существует вскрытие с выбранным открытым текстом, доказывающее, что xDES¹ не намного сильнее используемого в нем блочного алгоритма [858].

В xDES² эта идея расширяется до 5-этапного алгоритма, размер блока которого в 4 раза, а размер ключа в 10 раз превышают размеры блока и ключа используемого блочного шифра. На 1 lth показан один этап xDES², каж­дый из четырех подблоков по размеру равен блоку используемого блочного шифра, а все 10 ключей независимы.

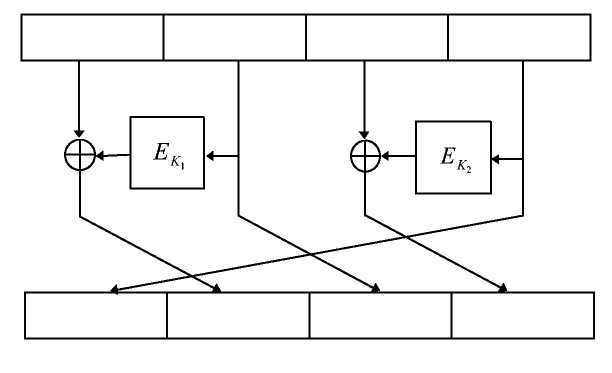
Рис. 15-4. Один 3TanxDES .

К тому же, эта схема быстрее, чем тройное шифрование: для шифрования блока, который в четыре раза больше блока используемого блочного шифра, нужно 10 шифрований. Однако этот метод чувствителен к диф­ференциальному криптоанализу [858] и использовать его не стоит. Такая схема остается чувствительной к диф­ференциальному криптоанализу, даже если используется DES с независимыми ключами этапов.

Для i ≥ 3 xDESⁱ вероятно слишком велик, чтобы использовать его в качестве блочного алгоритма. Например, размер блока для xDES³ в 6 раз больше, чем у лежащего в основе блочного шифра, ключ в 21 раз длиннее, а для шифрования блока, который в 6 раз длиннее блока лежащего в основе блочного шифра, нужно 21 шифрование .

Это медленнее, чем тройное шифрование.

Пятикратное шифрование

Если тройное шифрование недостаточно безопасно - может быть, вам нужно шифровать ключи тройного шифрования, используя еще более сильный алгоритм - то кратность шифрования можно увеличить. Очень ус­тойчиво к вскрытию "встреча посередине" пятикратное шифрование. (Аргументы, аналогичные рассмотренным для двойного шифрования, показывают, что четырехкратное шифрование по сравнению с тройным лишь незначительно повышает надежность.)

C = E_K1(D_K2(E_K3(D_K2(E_K1(P)))))

P = D_K1(E_K2(D_K3(E_K2(D_K1(C)))))

Эта схема обратно совместима с тройным шифрованием, если К₁= К₂, и с однократным шифрованием, если К₁= К₂ = К₃. Конечно, она будет еще надежней, если использовать пять независимых ключей.