1.Способи проходження графів

Для проходження нелінійних структур потрібно розробити стратегію доступу до вузлів і маркірування вузлів після обробки. Пошукові методи для бінарних дерев мають свої аналоги для графів. У спадному обході бінарного дерева застосовується така стратегія, при якій спочатку виконується обробка вузла, а потім уже просування вниз по піддереву. Узагальненням прямого методу проходження для графів є пошук "спочатку в глибину" (depth-first). Початкова вершина передається як параметр і стає першою оброблюваною вершиною. В міру просування вниз до тупика суміжні вершини запам'ятовуються в стеці, для того щоб можна було до них повернутися і продовжити пошук по іншому шляху у випадку, якщо ще залишилися неопрацьовані вершини. Оброблені вершини утворять безліч усіх вершин, досяжних з початкової вершини.

Характерне для дерев поперечне сканування починається з кореня, а обхід вузлів здійснюється рівень за рівнем зверху вниз. Аналогічна стратегія застосовується при пошуку "спочатку в ширину" (breadth-first) на графах,

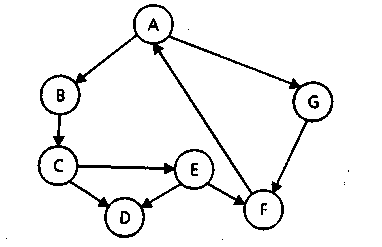
коли, починаючи з деякої початкової вершини, відбувається обробка кожної суміжної з нею вершини. Потім сканування продовжується на наступному рівні суміжних вершин і т.д. до кінця шляху. При цьому для запам'ятовування суміжних вершин використовується черга. Проілюструємо обох пошукових алгоритмів на наступному графі. У даному випадку початковою вершиною є А.

Пошук "спочатку в глибину". Для збереження оброблених вершин використовується список L, а для запам'ятовування суміжних вершин — стек S. Помістивши початкову вершину в стек, починається ітераційний процес виштовхування вершини зі стека і її обробки. Коли стек стає порожнім, процес завершується і повертає список оброблених вершин. На кожнім кроці використовується наступна стратегія.

Виштовхнути вершину V зі стека і перевірити за списком L, чи була вона оброблена. Якщо ні, зробити обробку цієї вершини, а також скористатися зручним випадком і одержати список суміжних з нею вершин. Уключити V у список L, щоб уникнути повторної обробки. Помістити в стек ті суміжні з V вершини, яких ще немає в списку L.

Пошук завершується після обробки вершини D.

Список L

Пошук "спочатку в ширину". Як і в поперечному проходженні бінарного дерева, при пошуку "спочатку в ширину" для збереження вершин використовується черга, а не стек. Ітераційний процес продовжується доти, поки черга не спорожніє.

Видалити вершину V з черги і перевірити її наявність у списку оброблених вершин. Якщо вершини V немає в списку L, уключити її в цей список. Одночасно одержати всі суміжні з V вершини і вставити в чергу ті з них, що відсутні в списку оброблених вершин.

Якщо застосувати цей алгоритм до розглянутого в попередньому прикладі графу, то вершини будуть оброблятися в наступному порядку: А В G С F D Е Мінімальний шлях. Методи проходження "спочатку в глибину" і "спочатку в ширину" знаходять вершини, досяжні з початкової вершини. При цьому рух від вершини до вершини оптимізується в змісті мінімального шляху. Шлях з мінімальною "вартістю"складається з ваг ребер, що складають шлях. Шляхи, що існують між двома вершинами, запам'ятовуються в черзі пріоритетів, що забезпечує прямий доступ до об'єкта з мінімальною вартістю.

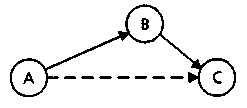
Наприклад, у показаному нижче графі між вершинами А и D існують три шляхи з різними вартостями.

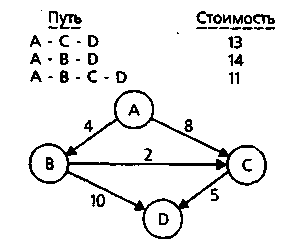
Алгоритм перевіряє шляхи, що зберігаються в черзі пріоритетів, і вибирає шлях із мінімальною вартістю.

Досяжність і алгоритм Уоршалла

Для кожної пари вершин деякого графа говорять, що Vj досяжно з Vi тоді і тільки тоді, коли існує спрямований шлях від Vi до Vj. Це визначає відношення досяжності R (reachability relation R). Для кожної вершини Vi пошук "спочатку в глибину" знаходить усі вершини, досяжні з Vi. При використанні пошуку "спочатку в ширину" виходить серія списків досяжності, що утворять відношення R: V ₁: <Список досяжності для V ₁ > V ₂: <Список досяжності для V ₂ > … Vn: <Список досяжності для V_n>

Це ж відношення можна також описати за допомогою матриці досяжності (reachability matrix) розміром n x n, що містить 1 у позиції (i,j), представляючи тим самим Vj R Vj. У наступному прикладі показані списки і матриця досяжності для зображеного тут графа.

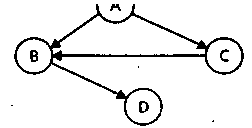
Списки досяжності Матриця досяжності

А: А В С D 1111

В: В D 0101

С: С В 0110

D: 0001

Матрицю досяжності можна використовувати для перевірки існування шляху між двома вершинами. Якщо елемент (i,j) дорівнює 1, то існує мінімальний шлях між V_i і Vj. Вершини в списку досяжності можна використовувати для нарощування ребер у вихідному графі. Якщо існує шлях з вершини v до вершини w (w досяжна з v), ми додаємо ребро E(v,w), що з'єднує ці дві вершини. Розширений граф G1 складається з вершин V графа G і ребер, що зв'язують вершини, що з'єднані спрямованим шляхом. Такий розширений граф називається транзитивним замиканням (transitive closure). Нижче приводиться приклад графа і його транзитивного замикання.

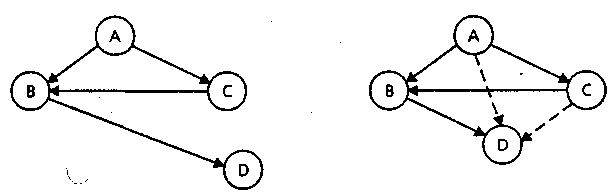
Більш витончений підхід застосовується в знаменитому алгоритмі Стефана Уоршалла. Матриця досяжності деякого графа може бути побудована шляхом присвоєння 1 кожній парі вершин, зв'язаних загальною вершиною. Припустимо, ми будуємо матрицю досяжності R і вершинам а, Ь, з відповідають індекси i, j, k. Якщо R[i][j] = 1 і R[j][k] = 1, установити R[i][j] = 1.

Алгоритм Уоршалла перевіряє всі можливі трійки за допомогою трьох вкладених циклів по індексах i, j і k. Для кожної пари (i,j) додається ребро Е( v _i , v _j ) , якщо існує вершина Vk, така, що ребра E(vi,Vk) і E(vk,Vj) знаходиться в розширеному графі. Повторюючи цей процес, ми з'єднуємо додатковими ребрами будь-яку пару досяжних вершин. У результаті виходить матриця досяжності.

Припустимо, що вершини v і w досяжні через спрямований шлях, щозв'язує п'ять вершин. Тоді існує послідовність вершин, що формують шлях V = Х_{1 ,} Х₂, Х₃, Х₄, Х₅ = W

Маючи шлях від v до w, ми повинні показати в матриці досяжності, що алгоритм Уоршалла зрештою дасть той же шлях. За допомогою трьох вкладених циклів ми перевіряємо всі можливі трійки вершин. Допустимо, вершини йдуть у порядку Х_1-Х5. У процесі перегляду різних трійок вершина Х₂ ідентифікується як загальний вузол, що зв'язує x_t і х₃. Отже, згідно алгоритму Уоршалла ми вводимо нове ребро Е(х_ьх₃). Для пари X ₁, X4 загальною сполучною вершиною є Хз, тому що шлях, що з'єднує Xi і Х₃, був знайдений на попередньому кроці ітерації. Тому ми створюємо ребро Е(х₁,х₄). У такий же спосіб х₄ стає загальною вершиною, що зв'язує Х ₁ і Х₅, і ми додаємо ребро Е(х₁,х₅) і привласнюємо елементу R[l][5] значення I

Проілюструємо алгоритм Уоршалла на наступному графі. Тут додаткові ребра, додані для формування транзитивного замикання зображені пунктиром.

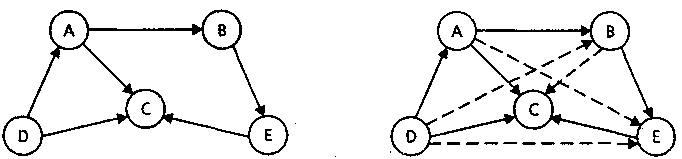
Вихідний граф Транзитивне замикання

Матриця досяжності

11101 01101 00100

11111

00101

Запити до захисту .

1. Визначення простого графа.

2. Шляхи в графі.

3. Критичний шлях в графі.

4. Для заданного графу побудувати матрицю суміжності.

5. Побудувати граф, відповідаючий заданій матриці суміжності.

6. Принципи обходу графа "спочатку в глубину".

7. Особливості обходу графа " спочатку в ширину".

8. Поняття досяжності вершини графу.