Лабораторна робота № 6 Розбудова в-дерева.

Мета роботи: Практично реалізувати В– дерево і основні операції над ним: формування, додавання і вилучення вузлів і т.і.

Зміст роботи та звіту.

1.Коротко описати особливості В - дерев і засоби їх відтворення

2.Розробити алгоритми основних операцій над В - деревами.

3.Реалізувати розроблені алгоритми програмою, відлагоджений текст якої подати до звіту. 4.Привести приклади результатів роботи програми.

Завдання :

Розробити програму реалізації основних операцій над В – деревами 2 –го порядку. Варіанти завдань відносно інформації в вузлах В - дерева: 1. Рядок фіксованої довжини. 2. Рядок як лінійний однозв’язаний список. 3. Рядок з рахівником довжини. 4. Рядок з ознакою кінця – символ %. 5. Рядок як лінійний двухзв’язаний список.

Короткі теоретичні відомості.

Вставка ключів у В-дерево.

Для виконання операції вставки ключа необхідно :

1. Переконатися , що аргумент пошуку не збігається з жодним із уже наявних у дереві ключів. Для цього необхідно, починаючи з кореня, послідовно переглядати вузли дерева , поки не буде досягнутий відповідний лист.

1. Якщо лист не заповнений цілком, зробити вставку аргументу у відповідне місце списку ключів і на цьому завершити операцію вставки.

2. Якщо в цьому листі вільного місця немає, то в результаті вставки число ключів стане рівним 2n+1 і виникне ситуація переповнення. При переповненні n+1 -й ключ ( середній ключ списку ) видалити з вузла; створити новий вузол ( лист ) і перемістити в нього n ключів списку з вузла, у якому виникло переповнення. Вилучений ключ вставити у вузол-корінь переповненого вузла. У такий спосіб при переповненні відбувається розщеплення вузла - утвориться два нових замість один старого і ключ переносу.

2 3 26 29

21 22 24 25

Вставка 24 у лист.

3. Якщо в результаті вставки ключа переносу внутрішній вузол виявиться переповненим , він теж розщеплюється ( при цьому половина списку ключів і списку покажчиків міститься в новий вузол ).

11 20

5 8 14 17

9 10 12 13

Вставка 12 у лист.

4. Якщо ключ переносу досягне кореня і він теж виявиться переповненим, його теж розщеплюють, що приводить до збільшення висоти дерева на одиницю і створенню нового кореня, куди і міститься ключ переносу. Отримані в результаті розщеплення 2 вузли стають коренями піддерев нового кореня.

Видалення

Для видалення ключа з В-дерева необхідно виконати наступні операції :

Знайти вузол, що містить ключ, що повинний бути вилучений. Подальші дії залежать від того, чи міститься ключ, що повинний бути вилучений, у листі чи нелистовому вузлі. 1. Випадок, коли ключ, що повинний бути вилучений, знаходиться в листі.

1. Якщо знайдений лист містить не менш ( n+1) ключів, то ключ просто видаляють з вузла й операцію закінчують.

2. Якщо в знайденому листі знаходиться рівно n ключів, тобто сусідній лист, що містить більш n ключів, то для збереження рівноваги досить виконати переміщення ключів із сусіднього листа. Для цього необхідно : видалити ключ, що розділяє списки ключів сусідніх листів, з вузла попереднього рівня і вставити його в лист, що містить ключів менше n; на місце вилученого ключа помістити крайній ( лівий чи правий ) ключ із сусіднього листа. У випадку великої нерівноваги числа ключів у сусідніх вузлах для зменшення числа балансувань дерева при наступних видаленнях краще переміщати одночасно максимально можливе число ключів ( до рівного чи приблизно рівного в сусідніх листах ).

5 9 14 17 Видалення ключа 7.

6 8 10 11 13

3. Якщо знайдений і сусідній з ним лист містять по n ключів, то роблять його конкатенацію - списки ключів сусідніх листів обединяются і залишається один лист, а іншої знищується.

5 8 14 Видалення ключа 18.

15 16 17 19

2. Випадок, коли ключ, що повинний бути вилучений, знаходиться в нелистовому вузлі :

   1. Видаляємо заданий ключ і поміщаємо на його місце ключ, що безпосередньо випливає по величині за вилученим. Вузол, що містить ключ, що безпосередньо випливає за вилученим, буде самим лівим листом правого піддерева вилученого ключа. Щоб знайти цей вузол, спускаємося вниз на один рівень по правому покажчику вилученного ключа і якщо це лист, то пошук закінчений. Інакше, використовуючи лівий покажчик поточного вузла, спускаємося вниз по дереву доти, поки не буде досягнутий лист. Тепер з листа видаляємо самий лівий ключ списку, що і буде безпосередньо наступним.

21 Результат видалення

ключа 8 і 20 з результат-

5 9 14 17 ного дерева

10 11 13 22 23 25

2. Наступні дії будуть аналогічні видаленню ключа з листа.

17

5 8 14 20 26

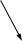
15 16 18 19 21 22 23 25 27 28 30 31

Запити до захисту.

10. Визначення В-дерева.

11. Залежність кількості ключів в вузлі від порядку В-дерева.

12. Опис вузла В-дерева.

13. Алгоритм формування В-дерева.

14. Додавання ключів до неповних вузлів В-дерева.

15. Додавання до листа В-дерева з сусідами – неповними вузлами.

16. Додавання до повного листа В-дерева.

17. Вилучення ключів з В-дерева.

Лабораторна робота № 7

Реалізація графа. Мета роботи: Практично реалізувати граф і основні операції над ним: формування, аналіз зв'язності, способи проходження,знаходження мінімального шляху, аналіз досяжності і т.і.

Зміст роботи та звіту.

1. Коротко описати граф як структуру даних і основних операцій над ним . 2. Розробити алгоритми основних операцій над графами.

3. Реалізувати розроблені алгоритми програмою, відлагоджений текст якої подати до звіту. 4. Привести приклади результатів роботи програми.

Завдання :

Розробити програму реалізації основних операцій над графом : 1. Формування. 2. Аналіз зв'язності. 3. Проходження графа способом "спочатку в глубину " і способом " спочатку в ширину". 4. Знаходження мінімального шляху між двома довільними вешинами. 5. Аналіз досяжності вершини з заданої.

Короткі теоретичні відомості.

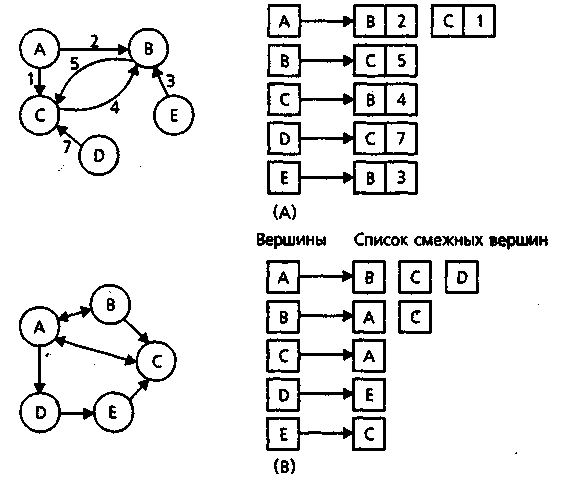
Представлення графів. Існує багато способів представлення орграфів. Можна просто зберігати вершини у виді послідовного списку Vo, Vi Vm-l, а ребра задавати квадратною матрицею розміром m*m, називаною матрицею суміжності (adjcency matrix). Тут рядок i і стовпець j відповідають вершинам Vi і Vj. Кожен елемент (i, j) цієї матриці містить вагу ребра Е _ij = (Vi, Vj) чи 0, якщо такого ребра немає. Для незваженого орграфа елементи матриці суміжності містять 0 чи 1, показуючи відсутність чи наявність відповідного ребра. Нижче приводяться приклади орграфов зі своїми матрицями суміжності.

В іншому способі представлення графів кожна вершина асоціюється зв'язаним списком суміжних з нею вершин. Ця динамічна модель зберігає інформацію лише об фактично приналежну графу вершинах. Для зваженого орграфа кожен вузол зв'язаного списку містить поле ваги. Приклади спискового представлення орграфов дані нижче.

Вершини Список суміжних вершин