Лабораторна робота № 4 Реалізація авл-дерева.
Мета роботи: Практично реалізувати основні операції над АВЛ - деревом : формування,балансування при додаванні і вилученні вузлів і т.і.
Зміст роботи та звіту.
1. Коротко описати основні методи балансування АВЛ - дерев.
2. Розробити алгоритми основних методів балансування.
3. Реалізувати розроблені алгоритми програмою, відлагоджений текст якої подати до звіту. 4. Привести приклади результатів роботи програми.
Завдання :
Розробити програму реалізації основних методів балансування АВЛ - дерев . Варіанти завдань відносно інформації в вузлах АВЛ - дерева: 1. Рядок з ознакою кінця – символ %; 2. Рядок як лінійний однозв’язаний список; 3. Рядок як лінійний двухзв’язаний список. 4. Рядок фіксованої довжини; 5. Рядок з рахівником довжини.
Короткі теоретичні відомості.
АВЛ-дерево – це бінарне дерево, в якому висота лівого і правого піддерева будь-якого вузла не відрізняється більще ниж на одиницю. Ця особливість оцінюється показником збалансованності вузла. Показник збалансованості вузла це різниця між висотою правого піддерева цього вузла і висотою лівого піддерева .
Ясно, що в АВЛ-дереві показник збалансованості усіх вузлів дорівнює чи —1, чи 0, чи +1. У цілком збалансованому дереві для усіх вузлів, за винятком максимум одного вузла, показник збалансованості дорівнює нулю. При додаванні ключа показник збалансованості вузла за абсолютним значенням може змінитися на 2 , порушуючи властивості АВЛ – дерева, тобто потрібне коректування структури дерева.
Мал.4.1. Показники збалансованності мають однаковий знак.
Наприклад, структура дерева разом з показниками збалансованості вузлів показана на мал. 4.1,a. Тут показник збалансованості вузла «4» є рівним -2 і умови АВЛ-дерева не задо-вольняються. Відновити баланс АВЛ-дерева, роблячи коректування його структури в межах цього піддерева,.можна зробити , якщо замість вузла «4» коренем цього піддерева вважати вузол «2», зробивши поворот вузлів «2» і «4» праворуч, як показано стрілкою.
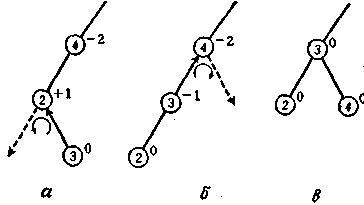
Мал.4. 2. Показники збаласованності мають різні знаки.
Для збалансування потрібно два повороти : перший-проти годинникової стрілки біля вузла "2", а другий – за годинниковою стрілкою відносно вузла "4"., показаний на мал.4. 2.,6.
Випадок, коли є декілька вузлів зпоказниками збалансованності однакового знаку (мал. 4.3., а)
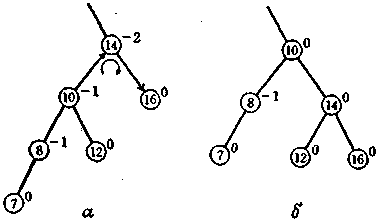
Мал. 4.3.
Збалансованість відновлюється,якщо виконати поворот відносно вузла «14» і перекріплення вузла «12» від вузла «10» до вузола «14» ( мал. 4.3,б ).
При
наявності послідовності вузлів з
показниками збалансованності різного
знаку
(мал. 4.4.а ), балансування, власне
кажучи, аналогічне показаним на мал.
4.2., тільки в цьому випадку також при
повороті вузол «11» необхідно відкріпити
від вузла
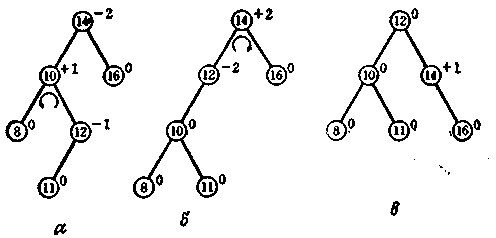
Мал. 4.4. «12» і прикріпити до вузла «10». Якщо спробувати узагальнити розглянуті випадки коректування структури дерева з метою балансування, то одержимо
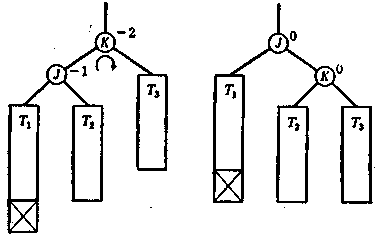
Мал. 4.5. Випадок, коли для відновлення балансу досить одного повороту.
діаграми, показані на мал. 4.5 і .6. На діаграмах прямокутниками позначені піддерева, « К » позначений самий нижній вузол, показник збалансованості якого після вставки по абсолютній величині стає більше 1, для вузла «К» і інших істотних вузлів показані значення їхніх показників збалансованості. Якщо після вставки показники збалансованості вузлів мають однаковий знак і відрізняються тільки на одиницю, як для вузлів « К» і «J» на мал. 4.5, то відновити баланс дерева можна однократним поворотом (включаючи одне переприкріплення піддерева), при цьому вставка не буде робити впливу на інші ділянки дерева. Якщо ж після вставки показники збалансованості мають різний знак, як для вузлів «K> і « I » на мал. 4.6 (тобто їх різниця по абсолютній величині дорівнює 3),то можна відновити баланс дерева дворазовими поворотами трьох вузлів, включаючи вузол « J» (використовуючи два перепри-кріплення піддеревв). У цьому випадку вставка також не робить впливу на інші ділянки дерева.
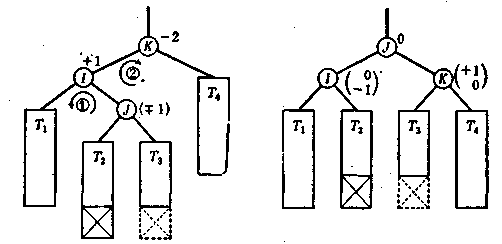
Мал. 4.6. Випадок, коли для відновлення балансу потрібно два повороту.
Запити до захисту.
Визначення АВЛ-дерева.
Визначення показника збалансованності вузла АВЛ-дерева.
Опис вузла АВЛ-дерева.
Алгоритм формування АВЛ-дерева.
Операція однократного оберта .
Операція двохкратного оберта .
Операція однократного оберта з перекріпленням.
Операція двохкратного оберта з перекріпленням.
Вилучення ключів з АВЛ-дерева.
Лабораторна робота № 5
Відтворення 2-3-дерева
Мета роботи: Практично реалізувати 2 – 3 – дерево і основні операції над ним: формування, додавання і вилучення вузлів і т.і.
Зміст роботи та звіту.
1.Коротко описати особливості 2 – 3 дерев і засоби їх відтворення
2.Розробити алгоритми основних операцій над 2 – 3 - деревами.
3.Реалізувати розроблені алгоритми програмою, відлагоджений текст якої подати до звіту. 4.Привести приклади результатів роботи програми.
Завдання :
Розробити програму реалізації основних операцій над 2 – 3 - деревами . Варіанти завдань відносно інформації в вузлах 2 – 3 - дерева: 1. Рядок як лінійний двухзв’язаний список. 2. Рядок фіксованої довжини. 3. Рядок як лінійний однозв’язаний список. 4. Рядок з рахівником довжини. 5. Рядок з ознакою кінця – символ %.
Короткі теоретичні відомості. Упорядковане дерево, кожен вузол якого містить 2 чи 3 зв'язку, а всі листи розташовані на одному рівні, називається (2—3)-деревом. З визначення випливає, що вузол (2—3)-дерева може містити один чи два ключі. Приклад такого дерева показаний на мал.5.1.
На мал. 5.2 показаний процес вставки в (2-3)-дерево для випадку порівняно великих змін. Ключ, що вставляється, завжди міститься в лист, але у випадку, коли лист уже містить два ключі, виконуються наступні дії.
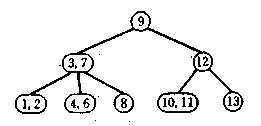
Мал. 5.1. Приклад (2—3)-дерева.
Ключ із середнім значенням перемещуєтьсявверх (видаляється із листа і включається в безпосередньо попередній вузол), а ключі, що залишилися, поділяються на два вузли. Якщо переданий знизу ключ потрапить у вузол, що вже містить два ключі, ключ із середнім значенням знову переміщується нагору, а вузол, що залишився, поділяється навпіл, утворюючи пару одноключевих вузлів. Такий підйом по рівнях може продовжуватися
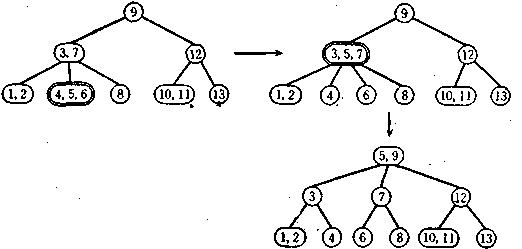
Мал. 5.2. Вставка в (2—3)-дерево.
аж до кореня, і якщо виявиться, що корінь містить два ключі, то висота дерева збільшується на одиницю. Оскільки (2—3)-дерева мають велику волю вузлів, чим АВЛ-дерева, зміна структури торкається меншої частини дерева і розщеплення вузлів виконується простіше, ніж балансування.
Видалення з (2—3)-дерев виявляється більш складним. У результаті видалення листа може трапитися, що в його початкового виявиться всього один породжений. Якщо цей породжений вузол містить два ключі, то один з них переміщається у початковий, а ключ початкового може бути опущений на місце вилученого листа. У випадку коли це не так, здійснюється наступна процедура.
Якщо по сусідству з початковим, утримуючим один ключ, мається вузол із двома ключами, то цей єдиний ключ переміщається на місце вилученого листа. При цьому виробляються переміщення нагору і вниз декількох ключів (мал. 6.4,a). Якщо по сусідству з вихідним вузлом, що містить один ключ, мається тільки одноключовий вузол (мал. 6.4,6), то два ключі опускаються, і сусідні вузли
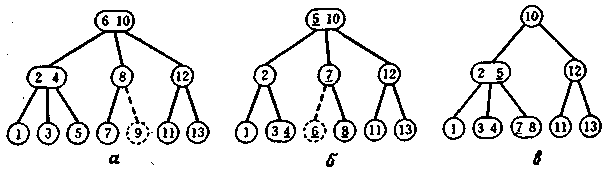
Мал. 5.3. Видалення з (2—3)-дерева. Підкреслено ключі, що переміщаються ( піднімаються чи опускаються) по рівнях дерева. Результатом видалення ключа 9 з дерева a, що має сусідній вузол із двома ключами, буде дерево б. Результатом видалення ключа 6 з дерева б, що не має сусіднього вузла з двома ключами, буде дерево в. При вилученні можуть поєднуватись два вузли, якщо в результаті вилучення у вузла-предка («діда») буде не більш одного ключа –послідовника, в якого тоже один послідовник ( наприклад, при вилученні ключа 11 ключі 12 і 13 поєднаються в один вузол) ; якщо вузол-«дід»— корінь, то при його видаленні рівень дерева понизиться, і ключ, що міститься в корені, може опуститися до листа. Хоча ідея переміщення ключів по дереву при видаленні досить проста, при написанні реальної програми можуть виникнути труднощі.
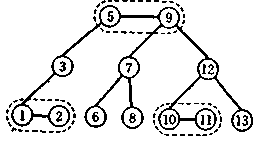
Мал. 5.4. Бінарне дерево пошуку, еквівалентне (2—3)-дереву на мал. 5.2.
Якщо для представлення вузлів із двома ключами (2—3)-дерева використовувати покажчики, то вони не будуть особливо відрізнятися від бінарних дерев пошуку (мал. 5.4). Для цього досить у кожен вузол увести прапорець, щоб відрізняти «горизонтальні» покажчики, що зв'язують перший ключ із другим, від «вертикальних» покажчиків другого ключа на праве піддерево. При пошуку немає необхідності в аналізі значення прапорця ( униз чи вправо) для класифікації покажчика. Зображена на мал. 5.4 структура несиметрична щодо лівого і правого ключів вузла. Для того щоб зробити представлення симетричним, досить у кожен вузол додати по одному покажчику: для першого (лівого) ключа ввести «вертикальний» покажчик на праве піддерево, для другого (правого) ключа ввести «горизонтальний» покажчик на перший (лівий) ключ. У випадку симетричного представлення (2—3)-дерево стає аналогічно АВЛ-дереву.
Запити до захисту.
Визначення 2-3-дерева.
Залежність між кількостю ключів в вузлі і кількістю наступників 2-3-дерева.
Опис вузла 2-3-дерева.
Алгоритм формування 2-3-дерева.
Додавання ключів до неповних вузлів 2-3-дерева.
Додавання до листа 2-3-дерева з сусідами – неповними вузлами.
Додавання до повного листа 2-3-дерева.
Вилучення ключів з 2-3-дерева.