5.5. Задача о конкурирующих супермаркетах

Три супермаркета конкурируют между собой с целью привлечения возможно большего количества покупателей. На 1 января известно распределение покупателей по супермаркетам в процентах. Фирма по изучению рынка подметила за прошлый год некоторые закономерности в средних ежемесячных переходах покупателей из одного супермаркета в другой. Эти переходы приведены в задании в виде процента сохранения своих покупателей и получения покупателей из других супермаркетов. Требуется сделать прогноз о возможном количестве покупателей в каждом супермаркете, предполагая общее число покупателей постоянным. Для этого необходимо

• построить граф и составить матрицу переходов для средних ежемесячных изменений количества покупателей,

• определить, какой процент покупателей будет иметь каждый супермаркет на 1 февраля,

• определить, какой процент покупателей будет иметь каждый супермаркет на 1 марта. Использовать для этого два способа расчета,

• найти процент покупателей для каждого супермаркета в установившемся режиме, составить для этого матричное уравнение и решить полученную систему линейных уравнений.

0. представить в табличном виде распределение покупателей по супермаркетам в динамике.

Пример. Решить задачу о супермаркетах для следующих данных. На 1 января магазин A посещало 35%, магазин B - 40%, а магазин C - 25% всех покупателей. За предыдущий год в среднем за месяц:

0. магазин A сохранил 80% своих покупателей и получил 10% покупателей магазина B и 2% покупателей магазина C;

1. магазин B сохранил 70% своих покупателей и получил 14% покупателей магазина A и 8% покупателей магазина C;

2. магазин C сохранил 90% своих покупателей и получил 6% покупателей магазина A и 20% покупателей магазина B

Р ешение. Будем рассматривать процесс переходов покупателей из магазина в магазин как цепь Маркова, который графически представлен на рис.10.

Рис.10. Граф переходов марковской цепи

Матрица переходных вероятностей имеет вид

.

По условию вектор начальных вероятностей равен ⁽⁰⁾=(0,35;0,40;0,25). Поэтому прогноз распределения покупателей на 1 февраля будет

.

Прогноз распределения покупателей на 1 марта будет

.

Этот прогноз можно получить также по формуле:

,

где

,

и, следовательно,

.

Для оценки состояния рынка в установившемся режиме необходимо решить систему уравнений . В матричном виде эта система уравнений имеет вид

,

откуда

, или .

Последняя система является неопределенной, причем 3-е уравнение является следствием 1-го и 2-го уравнений. Получим решение этой системы с учетом условия ₁+₂+₃=1, используя Microsoft Excel 7.0. В ячейки A2:C3 запишем коэффициенты первых двух уравнений системы, а в ячейки A4:C4 введем 1 (коэффициенты дополнительного условия). В ячейки E2:E4 занесем соответствующие свободные члены, как показано в табл.9.

Т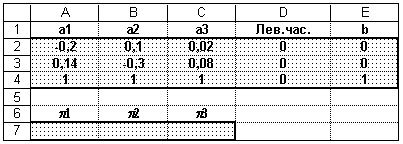 аблица 9

Предположим, что решение системы будет содержаться в ячейках A7:C7. В ячейки D2:D4 запишем формулы

D2=СУММПРОИЗВ(A2:C2;A7:C7),

D3=СУММПРОИЗВ(A3:C3;A7:C7),

D4=СУММПРОИЗВ(A4:C4;A7:C7).

О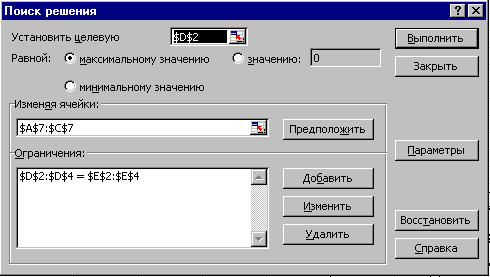 братившись к процедуре "Поиск решения" пункта меню "Сервис", следует заполнить надлежащие поля, как показано на рис.11.

Рис.11.

Нажатие кнопки "Выполнить" приводит к табл.10.

Т аблица 10

Таким образом, получено решение системы уравнений =(0,178;0,238;0,584).

Это значит, что при длительной работе магазин A будет посещать примерно 17,8% покупателей, магазин B - 23,8% покупателей, а магазин C - 58,4% всех покупателей города. Результаты расчетов сведены в табл.11.

Таблица 11

Распределение покупателей по супермаркетам в динамике

Дата	Посещаемость супермаркетов, %
	A	B	C
1 января	35	40	25
1 февраля	32,5	34,9	32,6
1 марта	30,1	31,6	38,3
…	…	…	…
Длительный срок	17,8	23,8	58,4

Из табл.11 следует снижение покупательской активности в супермаркетах A и B и увеличение покупательской активности в супермаркете C с 25% до 58,4%.