
- •1. Цель и задачи дисциплины
- •Тема 1. Теория вероятностей (8 час.)
- •Тема 2. Математическая статистика (6 час.)
- •Тема 3. Элементы теории графов и сетевого планирования (6 час.)
- •Тема 4. Математические модели конфликтных ситуаций (4 час.)
- •Тема 5. Математическое моделирование на основе теории случайных процессов (6 час.)
- •Тема 6. Понятие об имитационном моделировании (4 час.)
- •3. Учебно-методические материалы по дисциплине
- •10. Исследование операций в экономике. Под ред. Проф. Н.Ш.Кремера. М., «Банки и биржи», Издательское объединение «юнити», 1997.
- •4. Правила выполнения и оформления контрольных работ
- •5. Задачи для контрольных заданий
- •5.1. Теория вероятностей
- •5.2. Математическая статистика
- •5.3. Задача сетевого планирования
- •5.4. Задача о выпуске продукции при неопределенном спросе
- •5.5. Задача о конкурирующих супермаркетах
- •Содержание
- •1. Цель и задачи дисциплины 3
4. Правила выполнения и оформления контрольных работ
Изучение теоретической части курса «Математика в экономике» сопровождается выполнением контрольной работы. Исходные данные на работу выдаются преподавателем индивидуально каждому студенту. Данные можно получить также по номеру зачетной книжки через Internet. При выполнении контрольной работы студент должен соблюдать следующие требования.
Контрольная работа должна быть выполнена только в соответствии со своим вариантом, в отдельной тетради чернилами. Графики и рисунки изображаются карандашом.
На обложке тетради помещаются наименование дисциплины, фамилия и инициалы студента, факультет, курс, группа, код специальности, номер зачетной книжки, вариант.
Решение задач следует располагать в порядке возрастания их номеров. Перед решением каждой задачи надо полностью выписать ее условие, заменяя общие данные конкретными из соответствующего номера. Построение математических моделей и решение задач следует излагать подробно, объясняя все действия.
Пункты заданий, связанные с использованием компьютера, выполняются на кафедре математических методов и моделирования в экономике и управлении во время лабораторного практикума.
5. Задачи для контрольных заданий
5.1. Теория вероятностей
Задание по теории вероятностей предусматривает выполнение четырех задач. Методы решения этих задачи рассмотрены в [1] и [15].
Задача 1. Покупатель может приобрести акции трех компаний. Надежность первой компании в течение года оценивается экспертами на уровне a%, второй - на уровне b%, а третьей - на уровне c%. Чему равна вероятность того, что: а) все компании в течение года не станут банкротами; б) наступит хотя бы одно банкротство?
Пример. Решить задачу для следующих данных: a=90, b=80, c=70.
Решение. Обозначим события:
![]() - первая компания
в течение года не станет банкротом,
- первая компания
в течение года не станет банкротом,
![]() - вторая компания
в течение года не станет банкротом,
- вторая компания
в течение года не станет банкротом,
![]() - третья компания
в течение года не станет банкротом.
- третья компания
в течение года не станет банкротом.
По условию задачи вероятности этих событий равны:
![]() ,
,
![]() ,
,
![]() .
.
а) Событие
![]() ,
состоящее в том, что все три компании в
течение года не станут банкротами,
произойдет в том случае, если произойдет
и событие
,
и событие
,
и событие
.
Это значит, что событие
равно произведению событий
,
и
:
,
состоящее в том, что все три компании в
течение года не станут банкротами,
произойдет в том случае, если произойдет
и событие
,
и событие
,
и событие
.
Это значит, что событие
равно произведению событий
,
и
:
![]() .
.
Так как события , и являются независимыми, то по теореме умножения вероятностей вероятность произведения событий равна произведению вероятностей, то есть
![]() .
.
Подставляя числовые значения, получим
![]() .
.
Вероятность того,
что все компании в течение года не станут
банкротами равна
![]() .
.
б) Пусть
![]() - событие, состоящее в том, что наступит
хотя бы одно банкротство. Противоположное
событие состоит в том, что все компании
не станут банкротами, то есть
- событие, состоящее в том, что наступит
хотя бы одно банкротство. Противоположное
событие состоит в том, что все компании
не станут банкротами, то есть
![]() .
.
Поскольку сумма вероятностей противоположных событий равна 1, то
![]() .
.
Вероятность того,
что наступит хотя бы одно банкротство
равна
![]() .
.
Задача 2. Вероятность того, что новый товар будет пользоваться спросом на рынке, если конкурент не выпустит в продажу аналогичный продукт, равна p1. Вероятность того, что товар будет пользоваться спросом при наличии на рынке конкурирующего товара, равна p2. Вероятность того, что конкурирующая фирма выпустит аналогичный товар на рынок, равна q. Чему равна вероятность того, что товар будет иметь успех?
Пример. Решить задачу для следующих данных: p1=0,67, p2=0,42, q=0,35.
Решение. Обозначим события:
- событие, состоящее в том, товар будет иметь успех,
![]() - событие, состоящее
в том, что конкурент не выпустит в продажу
аналогичный товар,
- событие, состоящее
в том, что конкурент не выпустит в продажу
аналогичный товар,
![]() - событие, состоящее
в том, что конкурент выпустит в продажу
аналогичный товар.
- событие, состоящее
в том, что конкурент выпустит в продажу
аналогичный товар.
По условию задачи нам известны условные вероятности:
![]() ,
,
![]() .
.
Известна также
вероятность события
:
![]() .
События
и
являются несовместными и образуют
полную группу (являются гипотезами),
поэтому сумма вероятностей этих событий
равна 1:
.
События
и
являются несовместными и образуют
полную группу (являются гипотезами),
поэтому сумма вероятностей этих событий
равна 1:
![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() .
.
Для определения вероятности события применим формулу полной вероятности:
![]() .
.
Подставляя числовые значения, получим
![]() .
.
Вероятность того,
что товар будет иметь успех, равна
![]() .
.
Задача 3. В ходе аудиторской проверки строительной компании аудитор случайным образом отбирает n счетов. Известно, что a% счетов содержат ошибки. Требуется
составить таблицу распределения вероятностей числа правильных счетов,
найти числовые характеристики этого распределения,
записать функцию распределения вероятностей и построить ее график,
определить вероятность того, что хотя бы 1 счет будет с ошибкой.
Пример. Решить задачу для следующих данных: n=4, a=27.
Решение.
Число правильных счетов есть случайная
величина X,
которая может принимать значения: 0, 1,
2, 3, 4. Вероятности этих значений определим
по формуле Бернулли:
![]() ,
где
,
где
![]() - вероятность неправильного счета, а
- вероятность неправильного счета, а
![]() - вероятность правильного счета. Получим
- вероятность правильного счета. Получим
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Сделаем проверку.
Сумма вероятностей должна быть равна
1. Действительно,
![]() .
.
Распределение вероятностей случайной величины X содержится в табл.1.
Таблица 1
Распределение случайной величины X
![]()
Определим числовые характеристики этого распределения. Математическое ожидание дискретной случайной величины X находим по формуле
![]() ,
,
где
![]() - возможные значения X,
а
- возможные значения X,
а
![]() - соответствующие вероятности.
- соответствующие вероятности.
![]()
Дисперсию случайной величины X находим по формуле
![]() .
.
Так как
![]() ,
,
то
![]() .
.
Среднее квадратическое отклонение случайной величины X равно
![]() .
.
Найдем функцию
распределения вероятностей
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Е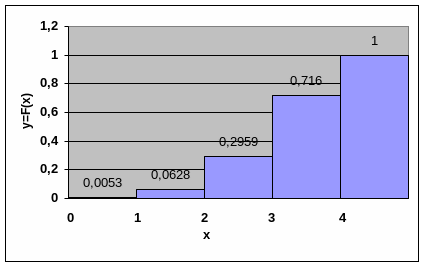 сли
сли
![]() ,
то
,
то
![]() .
.
График функции
![]() изображен на рис.1.
изображен на рис.1.
Рис.1. График функции распределения
Событие A, состоящее в том, что хотя бы 1 счет будет с ошибкой, является противоположным к событию, что все счета будут правильными, следовательно,
![]() .
.
Вероятность того,
что хотя бы 1 счет будет с ошибкой, равна
![]() .
.
Задача 4. Годовой выпуск продукции мебельной фабрики приблизительно распределен по нормальному закону со средним значением, равным m тыс.ед. продукции, и стандартным отклонением - тыс.ед. Найти вероятность того, что годовой выпуск продукции: а) окажется ниже b тыс.ед.; б) превысит a тыс.ед.
Пример. Решить задачу для следующих данных: m=134, =13, b=100, a=150.
Решение. Обозначим
через X - годовой выпуск продукции
мебельной фабрики. Это непрерывная
случайная величина, имеющая нормальное
распределение с параметрами m
и .
Поэтому вероятность попадания случайной
величины в промежуток [a,
b]
вычисляется по формуле
![]() ,
,
где
![]() -
-
функция Лапласа,
которую можно вычислить как по таблицам,
так и с помощью программы Microsoft
Excel.
Если в ячейку A1
записано значение
![]() ,
то формула B1=НОРМРАСП(A1;0;1;ИСТИНА)
запишет в ячейку B1
соответствующее значение функции
Лапласа
,
то формула B1=НОРМРАСП(A1;0;1;ИСТИНА)
запишет в ячейку B1
соответствующее значение функции
Лапласа
![]() .
.
Вероятность того, что годовой выпуск продукции окажется ниже b=100 тыс.ед.:
![]()
Вероятность того, что годовой выпуск продукции превысит b=150 тыс.ед.:
![]() .
.
Таким образом, с большой вероятностью годовой выпуск продукции будет находиться между 100 и 150 тыс.ед.
