
- •Глава 1
- •1.1. Обобщенное описание задачи
- •1.2. Объекты управления
- •1.3. Принципы цифрового управления
- •1.4. Математические модели цифровых систем управления
- •1.5. Вычислительные методы решения задач
- •4. Ос рв с полным сервисом.
- •Глава 3
- •Глава 4
- •4.3. Нанокомпьютеры
- •5Л. Микропроцессорная система управления электродвигателем
- •5.2. Нечеткая адаптивная система
- •Получим выражение для уравнения движения атс. Для разложим в ряд Тейлора и используем линейные члены:
- •При малых отклонениях (в установившемся режиме)
- •Представим это выражение в безразмерном виде:
- •Поэтому передаточная функция атс при управлении скоростью с помощью механизма топливоподачи будет
- •5.3. Нечеткая система управления
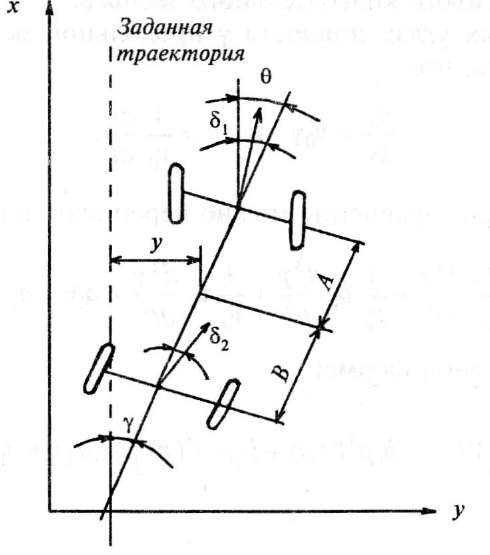
- •Структурная схема системы управления атс будет выглядеть, как показано на рис. 5.43.
- •Окончание табл. 5.3
- •5.4. Управляющий вычислительный комплекс радиотелескопа
5.3. Нечеткая система управления
углом поворота автомобиля
Управление движением АТС по заданной траектории, т. е. управление текущими координатами колесных транспортных средств, осуществляется путем поворота управляемых колес. При управлении курсом движения передаточные функции колесного АТС будут:
![]()
где
Y(p)
—
изображение по Лапласу линейного
отклонения,
![]() (p)
— изображение
по Лапласу угла поворота продольной
оси АТС,
B(p) — изображение
по Лапласу угла поворота управляемых
колес.
(p)
— изображение
по Лапласу угла поворота продольной
оси АТС,
B(p) — изображение
по Лапласу угла поворота управляемых
колес.
Линеаризованное уравнение движения АТС по криволинейной траектории, полученное из расчетной схемы (рис. 5.44), имеет вид
![]()
В
этом уравнении приняты следующие
сокращения:
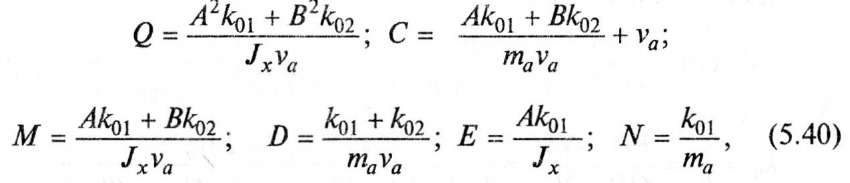
где А и В — расстояния от центра тяжести до переднего и заднего мостов; к01 и к02 — коэффициенты сопротивления уводу переднего и заднего мостов, Jz момент инерции автомобиля вокруг вертикальной оси, проходящей через центр тяжести ТС; va — скорость движения; та — масса ТС.
Запишем указанное уравнение в оперативной форме:

Рис.
5.41. Схема транспортного средства
Передаточная
функция колесного АТС при управлении
направлением движения будет:
T1
, T2—
постоянные времени,
Таким
образом, АТС можно представить состоящим
из последовательного соединения
интегрирующего, дифференцирующего
и устойчивого колебательного звеньев.
При
малых углах поворота у продольной оси
автомобиля можно считать, что
Тогда
второе уравнение можно переписать в
виде
или
в операторной форме:

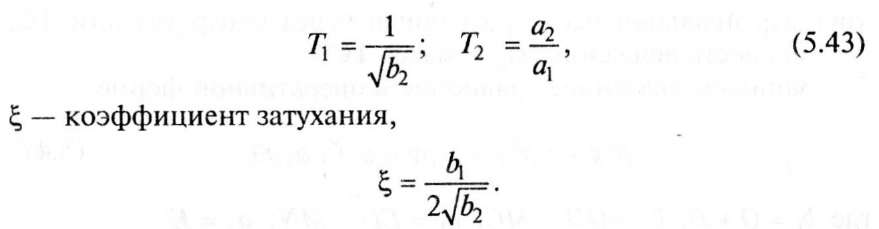
![]()
![]()
![]()
Передаточная функция, определяющая зависимость поперечного отклонения ТС от угла поворота управляемых колес, будет
Коэффициенты к0, k1 e и постоянные времени Т1 и Т2 зависят от конструктивных параметров рулевых управлений АТС. Из графиков (рис. 5.42) видно, что коэффициент преобразования к0, кх и постоянные времени Тх, Т2 АТС зависят как от скорости движения, так и от нагрузки на АТС.
Если
учесть, что, как правило, величина
Т1>>Т2
и
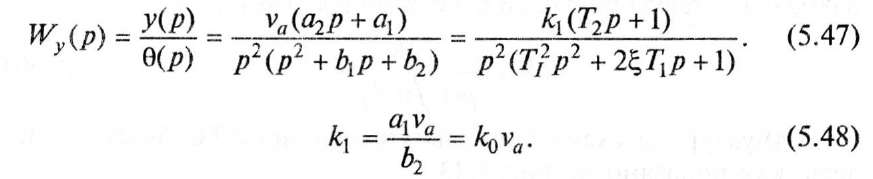
![]() ,
то получим следующие выражения:
,
то получим следующие выражения:![]()
Рис.
5.42. Зависимость коэффициента преобразования
и постоянной времени от скорости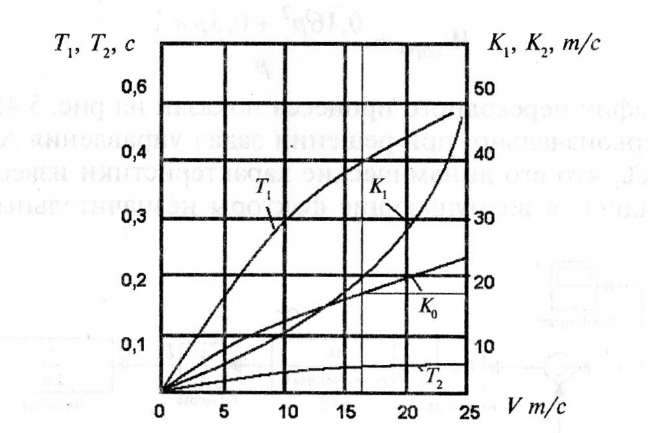
Из данного графика получаем, что при скорости 60 км/ч (16,66 м/с) коэффициент к0 будет равен 18, а постоянная времени T1 равна 0,4. Отсюда получаем передаточную функцию:
![]()
Структурная схема системы управления атс будет выглядеть, как показано на рис. 5.43.
Рис.
5.43. Структурная схема системы управления
АТС
Промоделируем систему управления курсом движения АТС в системе Simulink. На рис. 5.44 представлена модель системы управления курсом движения АТС.
В качестве регулятора можно использовать ПИД-регулятор с передаточной функцией:
![]()
График переходного процесса показан на рис. 5.45. Первоначально, при решении задач управления АТС предлагалось, что его динамические характеристики известны и не изменялись, а возмущающие факторы незначительны. Однако
Рис.
5.44. Модель управления курсом движения
АТС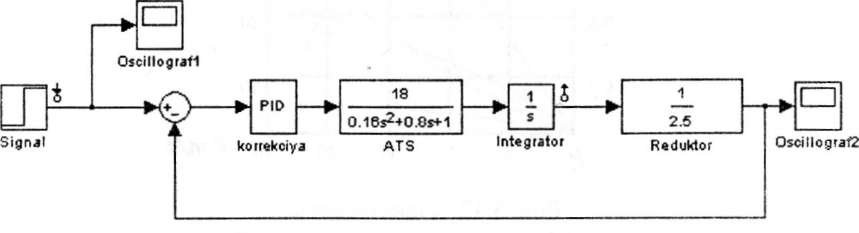
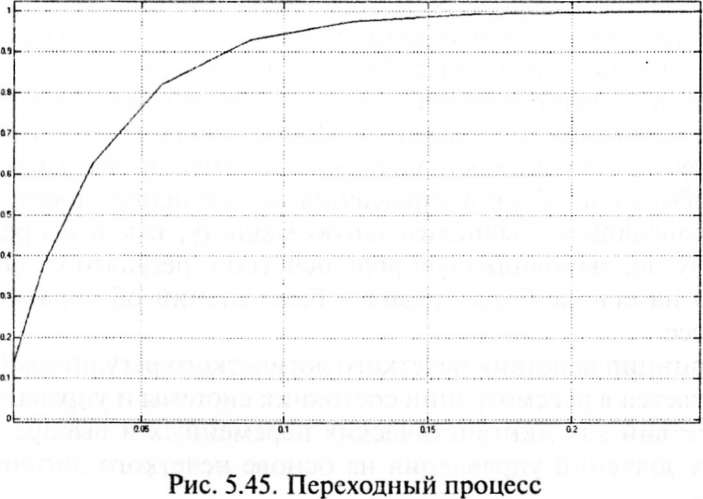
динамические характеристики автомобиля меняются в зависимости от переключения передачи и нагрузки, другими словами, они различны при различных передачах, нагрузках и состояниях дороги. Кроме того, существенное влияние на них оказывает обстановка на дороге. Поэтому изначально настроенные параметры регулятора системы на некий оптимум при изменении дорожных условий перестают быть оптимальными.
Требуемую коррекцию системы можно произвести двумя способами:
изменением коэффициентов настройки регулятора;
введением в систему дополнительного корректирующего управляющего сигнала.
425
Особенностями нечеткого управления являются возможность представления техники и знаний о вождении, которыми обладает водитель, с помощью лингвистических правил управления, что позволяет во многих случаях обойтись без количественной модели объекта управления. Поэтому в качестве устройства управления с функциями адаптации к изменениям параметров автомобиля как объекта управления можно использовать такую же управляющую вычислительную машину, как и в предыдущем случае, выполняющую роль нечеткого регулятора, построенного на основе базы правил и базы знаний об управляемом процессе.
Принцип действия нечеткого логического регулятора (HJIP) заключается в рассмотрении состояния системы и управляющих воздействий как лингвистических переменных и выборе конкретных значений управления на основе нечеткого логического вывода.
На вход устройства поступает "четкая" исходная величина, которая фазификатором преобразуется в нечеткое множество (или лингвистическую переменную). Далее машина вывода на основе нечеткой базы знаний производит обработку входных величин, и полученное нечеткое множество в блоке дефазификации отображается в четкую выходную величину, используемую для управления объектом. Естественно, в общем случае нечеткий логический регулятор может содержать не один фазификатор, если необходим ввод нескольких параметров, и не один дефазификатор, если необходимо несколько управляющих воздействий на объект.
Нечеткий алгоритм управления может быть реализован различными программными средствами.
Первый способ — написание программы на языке высокого уровня. При вычислении лингвистической переменной и ее функции принадлежности вполне достаточно использование тех операторных средств и математического аппарата, которыми располагает практически любой язык программирования.
Основой программы является использование операторов условного перехода (операция импликации) "если — то". Если выполняется заданное условие, то осуществляется одна операция, если нет — другая.
Второй способ — использование оболочек экспертных систем. Нечеткий регулятор можно реализовать в виде правил "если — то", реализовав их в оболочке экспертной системы.
Третий способ — использование нейронной сети. При реализации нечетких регуляторов в виде нейронной сети используют принципиально другой подход, основанный на обучении нейронной сети к распознаванию той или иной ситуации выбора. Это касается всех основных процессов: фазификации, логического вывода и дефазификации.
Когда при построении системы управления учтены все факторы, значения которых известны, тогда систему можно рассчитать достаточно точно, но как только появляются условия неопределенности, тогда возникает необходимость ввода в систему корректировки, зависящей от времени. Такими неопределенностями являются дорожные условия.
Дорожные условия — совокупность геометрических характеристик транспортно-эксплуатационных средств несущего основания (дороги, местности) непосредственно, в основном механически влияющих на возможности и параметры движения АТС.
Основными геометрическими характеристиками несущего основания являются: продольный и поперечный профиль трасс, частота поворотов и радиусы кривизны в плане, ширина трасс, длина их прямых и криволинейных участков.
На движение АТС оказывают существенное влияние такие факторы, как: покрытие дороги (асфальт, грунт, и т. д.), погодные условия (влажность температура).
Погодно-климатические условия характеризуют состояния воздушной среды, окружающей АТС, и ее изменения, связанные с природными явлениями. Воздушная среда играет заметную роль в формировании динамики, управляемости и безопасности движения АТС. Температура, влажность и давление воздуха существенно влияют на работу силовой установки, ходовой части и элементов систем управления. Под действием метеорологических факторов могут измениться условия информационного обеспечения движения, дорожные условия и дорожная обстановка. Сопротивление воздуха, особенно при скоростях движения более 30 км/ч, составляет заметную часть общего сопротивления движению АТС.
Особенно значимыми для работы систем автоматического управления могут быть неблагоприятные погодные факторы: осадки, сильный ветер, пониженная температура воздуха, снижение прозрачности атмосферы.
Неблагоприятные погодно-климатические условия можно охарактеризовать метеорологическими показателями, их воздействием на движение АТС, частотой проявления и изменения, длительностью действия на АТС в данный момент или по отношению к общему времени эксплуатации АТС.
Наибольшее влияние на движение АТС оказывают осадки в виде дождя и снега. Они опасны не только в момент выпадения, но и отдаленными последствиями. Так, например, вследствие осадков дорожное покрытие изменяет свои свойства. Ухудшаются его сцепные качества, а сопротивление движению возрастает. При пониженных температурах возможно также за- снеживание, сужение проезжей части, обледенение дорог. Снежный покров изменяет очертания местных предметов, скрывает препятствия, изменяет контрастдорог и обочины. Все это ведет к изменению алгоритмов и усложнению управления машиной При расчете автоматической системы управления движением (АСУД) необходимо их учитывать. Если мы создаем систему на основе экспертных систем, то по входным данным, снимаемым с датчиков, необходимо создать набор правил, например, при учете трех параметров: влажность (к), температура (?) и покрытие (m), нам необходимо на основе численных значений этих коэффициентов задать один общий корректирующий коэффициент z-
Далее,
из всех возможных комоинации создаются
правила в виде импликаций:
![]()

Коэффициенты а, b и с добавляются в регулятор, в качестве корректирующих коэффициентов.
Но в вышеописанных случаях получается грубая корректировка. Для получения более точных решений, необходима более мелкая дискретизация коэффициентов условий неопределенности и выбор конкретных значений управления на основе нечеткого логического вывода.
Для коррекции системы в зависимости от изменения внешних условий воспользуемся методом лингвистических переменных и написания для этого метода программы на языке высокого уровня.
Программа будет по существу нечетким регулятором самонастройки параметров основного регулятора в виде правил, которые в зависимости от входных переменных в виде численных значений параметров внешних условий будут выдавать необходимые параметры основного регулятора системы. Сама система смоделирована в пакете прикладных программ (ППП) MathLab 7.0 (рис. 5.46). Программа, реализующая регулятор, написана на языке Pascal 7.0. Для удобства тестирования и получения результатов также написан аналог этой программы на языке MathLab. Программа вычисляет три коэффициента ПИД-регу- лятора.
Коэффициент
Y.
добавляется
в систему в качестве корректирующего
дополнительного управляющего сигнала.
Второй
способ корректировки заключается во
введении дополнительных корректирующих
коэффициентов в регулятор. В зависимости
от
к, t
и
т
мы получаем набор правил:![]()

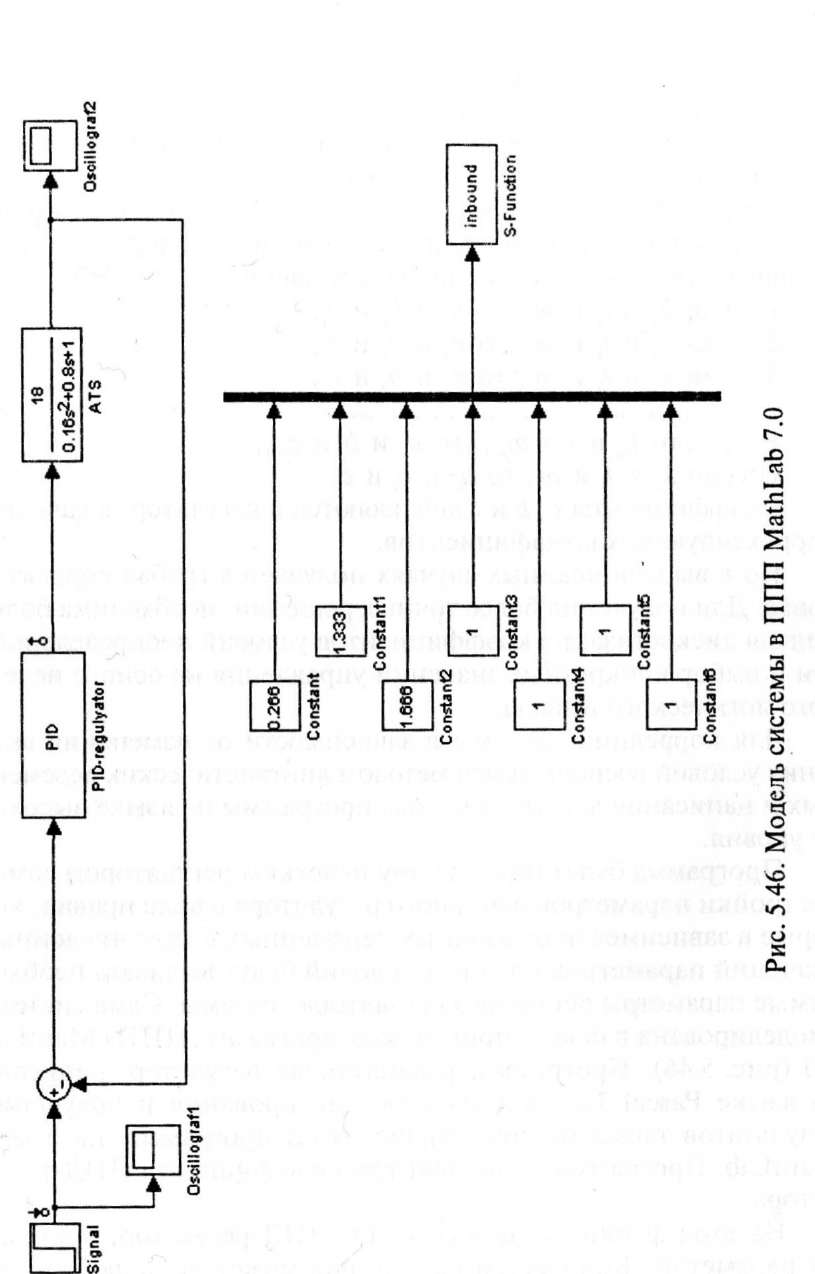
работы программы и количества возможных комбинаций состояния системы, а уменьшение приводит к потере точности отработки системы. Для моделирования системы возьмем семь параметров. Каждый из этих параметров разбит в функции на пять градаций и приравнивается к наиболее близкому значению, после чего по данным семи значений выбирается одно правило, в котором рассчитаны коэффициенты ПИД-регулятора. Впоследствии они и корректируют систему. Так как правил для этой системы при семи параметрах получается большое количество, то приведем в табл. 5.3 набор лишь из нескольких правил, где, в зависимости от семи параметров вычислены коэффициенты ПИД-регулятора.
Таблица
5. 3 Примеры
вычисленных коэффициентов ПИД-регулятора
т
А
V
R
Т
Р
Кр
Кi
КD
~800
-10
20
20
0
80
571,55933
766,96
257,2908
800
-5
10
15
-5
40
243,84933
319,12
104,4056
800
-5
25
50
5
100
842,10533
1072,00
341,1643
800
0
15
50
-2
80
315,126
391,39
121,5256
800
0
20
30
2
40
352,73967
513,16
186,6319
870
5
25
100
-5
100
354,58367
548,35
212,0002
870
10
10
50
-5
40
174,96367
203,79
59,34203
950
-10
5
30
2
100
689,40567
453,14
74,4604
1040
-10
15
15
-2
100
922,56667
1010,87
276,9043
1040
0
5
100
5
100
572,61167
319,05
44,44257
1040
5
10
50
-2
40
322,53833
322,34
80,5372
1150
-10
15
100
5
20
937,14567
854,70
194,8756
800
-10
10
50
-5
20
336,51543
332,76
82,2619
800
-10
20
50
5
20
951,8144
1044,07
286,315
800
-5
20
15
-5
60
505,0877
725,44
260,4795
800
10
20
20
5
20
447,90827
638,80
227,7635
870
-10
15
20
2
80
1494,865
1385,29
320,9357
950
-10
5
100
5
60
1096,8644
519,07
61,4105
