
- •Глава 1
- •1.1. Обобщенное описание задачи
- •1.2. Объекты управления
- •1.3. Принципы цифрового управления
- •1.4. Математические модели цифровых систем управления
- •1.5. Вычислительные методы решения задач
- •4. Ос рв с полным сервисом.
- •Глава 3
- •Глава 4
- •4.3. Нанокомпьютеры
- •5Л. Микропроцессорная система управления электродвигателем
- •5.2. Нечеткая адаптивная система
- •Получим выражение для уравнения движения атс. Для разложим в ряд Тейлора и используем линейные члены:
- •При малых отклонениях (в установившемся режиме)
- •Представим это выражение в безразмерном виде:
- •Поэтому передаточная функция атс при управлении скоростью с помощью механизма топливоподачи будет
- •5.3. Нечеткая система управления
- •Структурная схема системы управления атс будет выглядеть, как показано на рис. 5.43.
- •Окончание табл. 5.3
- •5.4. Управляющий вычислительный комплекс радиотелескопа
Тогда
![]()
Получим выражение для уравнения движения атс. Для разложим в ряд Тейлора и используем линейные члены:

При малых отклонениях (в установившемся режиме)
![]()
![]()
Представим это выражение в безразмерном виде:
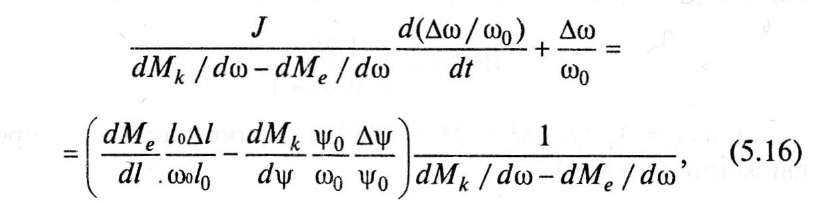
где
I0
и
![]() 0
— положение механизма торможения и
сопротивление нагрузки, соответствующие
скорости вращения
0.
0
— положение механизма торможения и
сопротивление нагрузки, соответствующие
скорости вращения
0.
При постоянной величине сопротивления нагрузки Ay = 0 правая часть уравнения запишется в виде:
т. е. АТС обладает статическими свойствами, характеризуемыми величиной к0, и инерционностью, характеризуемой T0.
где
T0
—
постоянная времени; k0
—
передаточный коэффициент. В операторном
виде
Для
(
0
=
33 1/с,
Me
= Mk
=
1350
Н-м (соответствует скорости движения
60 км/ч)
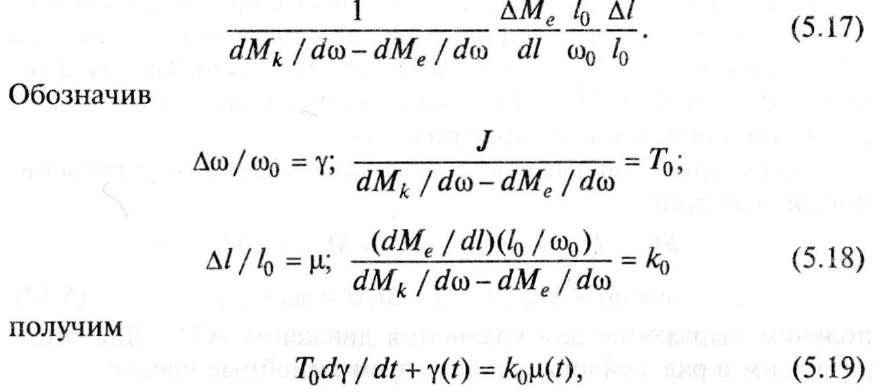
![]()
Поэтому передаточная функция атс при управлении скоростью с помощью механизма топливоподачи будет
![]()
![]()
![]()
Для 0 = 50 1/с, Me = Mk = 1350 Нм, (соответствует скорости движения 90 км/ч)
![]()
(5.24)
В разрабатываемой цифровой системе управления вполне можно использовать такой же модуль центрального процессорного устройства CPU 686Е, как и в предыдущем примере.
Для выбора преобразователей (ЦАП и АЦП) определим два основных параметра: минимальное число разрядов и быстродействие.
![]()
(5.25)
Значит, дчя выполнения условия по точности системы достаточно 8 разрядов преобразователя.
Быстродействие системы должно быть не хуже t = 0,01Т. Поэтому выберем ЦАП и АЦП с временем преобразования не более 5*104с.
При этом получим коэффициент усиления АЦП из условия, что 28= КАЦП Т, где KАЦП — коэффициент усиления АЦП. Откуда KАЦП = 256.
Коэффициенты усиления ЦАП из условия, что 1 / 28= K ЦАП =
= 1/256, где K ЦАП — коэффициент усиления ЦАП.
Структурные схемы моделей АЦП и ЦАП показаны на рис. 5.18.
Рис.
5.18. Структурная схема АЦП или ЦАП:
Gain
—
коэффициент передачи, равный 256;
Quantizer
— квантователь
с уровнем 1/256; Delay
— задержка,
равная 1/100000 с
Структурная схема цифровой системы управления показана на рис. 5.19
![]()
где Кp , KI- коэффициенты пропорциональной и интегральной составляющих.
Идея ПИ-регулятора является эмпирической: пропорциональная составляющая отражает ошибку системы в настоящий момент времени, интегральная составляющая — историю изменения ошибки системы.
Рассмотрим настройку ПИ-регулятора для различных рабочих точек.
![]()
Рис.
5.19. Структурная схема цифровой системы
стабилизации скорости АТС:
Wreg (p)— передаточная функция регулятора скорости; DAC — ЦАП; WE(p) - передаточная функция двигателя; ADC — передаточная функция АЦП; V— задающее воздействие; U— сигнал с регулятора скорости; W- скорость; E = V— W
и переходный процесс в системе с данной настройкой ПИ- регулятора будет как на рис. 5.20.
Для рабочей точки, соответствующей передаточной функции (5.23), настройка регулятора будет
![]()
и переходный процесс будет как на рис. 5.21.
Для рабочей точки, соответствующей передаточной функции (5.24), настройка регулятора будет
![]()
и переходный процесс будет как на рис. 5.22.
Таким образом, для каждой рабочей точки графика, т. е. для различных рабочих режимов, необходима своя настройка регулятора, если настройку регулятора не менять, то поведение системы будет нестабильно, как это видно из рис. 5.23 (показан переходный процесс системы при скорости движения 10 км/ч, с регулятором, настроенным на скорость движения 90 км/ч).
Рис.
5.20. Переходный процесс в системе
стабилизации с настроенным ПИ-регулятором,
при скорости движения W=
20
км/ч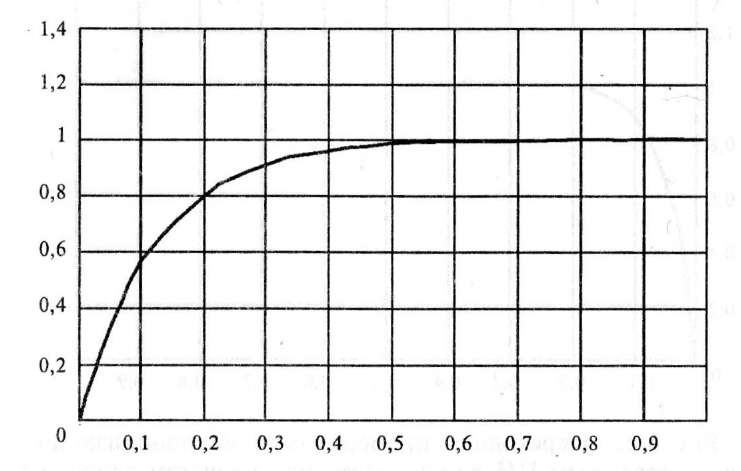
Рис.
5.21. Переходный процесс в системе
стабилизации с настроенным ПИ-регулятором,
при скорости движения w
=
60 км/ч
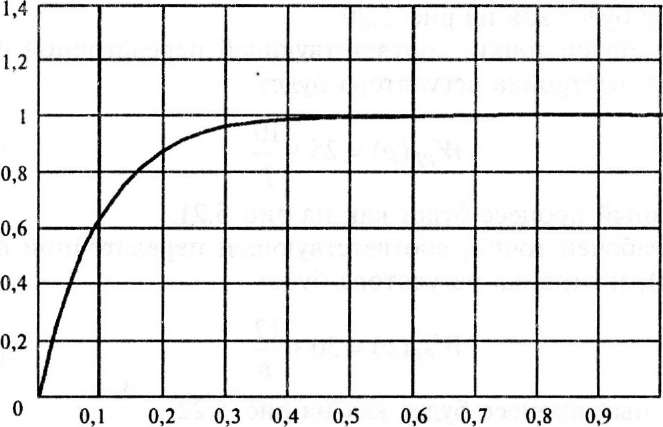
Рис.
5.23. Переходный процесс в системе
стабилизации с настроенным ПИ-регулятором
для скорости движения 90 км/ч, при
скорости движения w = 10
км/ч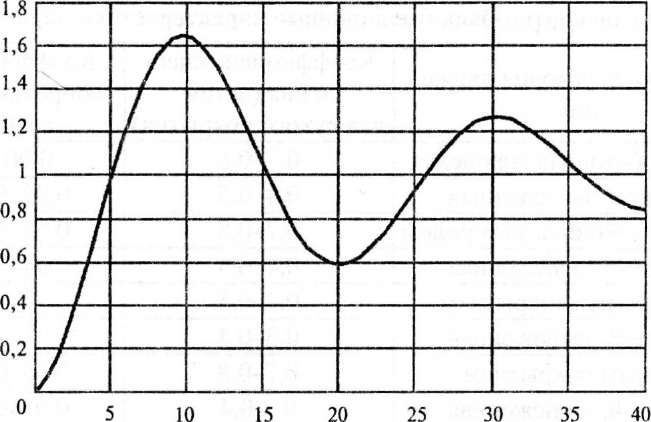
Следовательно, невозможно достичь желаемого качества регулирования при использовании фиксированной настройки регулятора, и при изменении скорости движения АТС настройку регулятора необходимо менять.
Теперь проведем исследование системы при воздействии на объект управления возмущения в виде дополнительного момента сопротивления, приводящего к изменению скорости движения (табл. 5.2).
Кинематические, силовые и информационные связи АТС с внешней средой, приводящие к изменению скоростного режима, которые необходимо учитывать при разработке и создании систем автоматического управления, интегрально можно охарактеризовать результирующими воздействиями на АТС в процессе движения. Кинематические связи АТС с внешней средой влияют на положение, величину и распределение ряда внешних нагрузок, скорости и ускорения движения АТС, сопутствующего перемещению в основном направлении.
Кинематические связи АТС характеризуются геометрическими показателями трасс (продольным и поперечным профилем, кон-
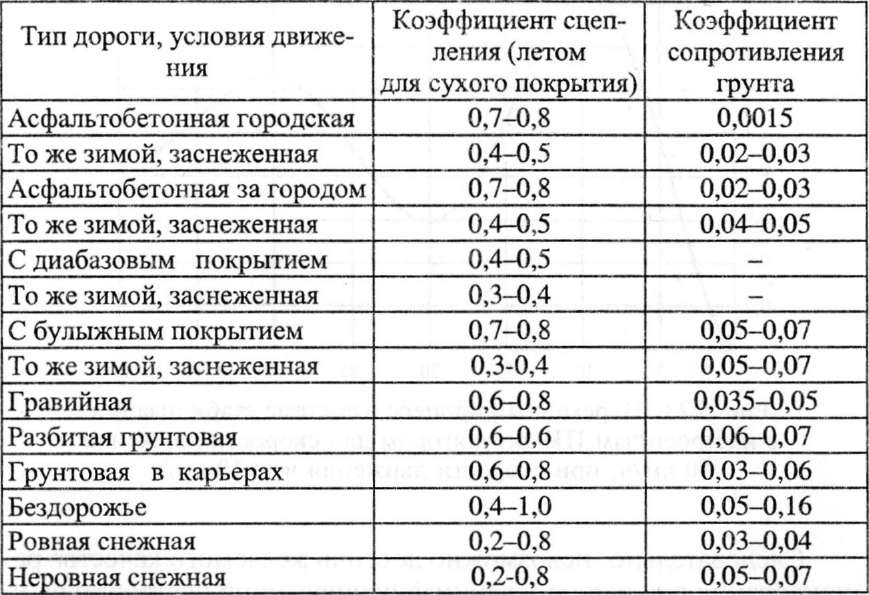
Таблица
5. 2
Транспортно-эксплуатационные
характеристики дорог
фигурацией в плане) и микропрофилем, влияющим на изменение положения в основном в продольной и поперечной вертикальных плоскостях и движение АТС.
Статическое изменение положения АТС сопровождается появлением продольных и поперечных составляющих сил тяжести и соответствующих им реакций несущего основания, уменьшением нормального давления и нормальных реакций грунта. Их величина в соответствии с данными, приведенными в таблице, можетдостигать в статике 30—60 % от величины исходных нормальных реакций грунта — для продольных и поперечных сил и в среднем от 70 до 150 % — для опорных реакций грунта АТС. Соответственно будут изменяться продольные и поперечные силы сцепления и сопротивления движению, а также боковые реакции несущего основания. В движении к статическому изменению сил будут добавляться силы и моменты инерции, препятствующие изменению положения и режима движения
АТС, центробежные силы (и соответственно боковые реакции несущего основания), а также кориолисовы силы в случае сложного движения АТС. Величина этих сил и моментов зависит не только отусловий, но и отрежимовдвижения, интенсивности их изменения, массы транспортного средства, свойств несущего основания и ряда других факторов. Их конкретные зависимости и взаимосвязи дает теория автомобиля. Здесь же достаточно сказать, что величина этих сил в ряде случаев может превосходить тяговые и сцепные свойства АТС, что, как правило, ведет к нарушению устойчивости и неуправляемому движению АТС.
В процессе проектирования автоматизированных АТС такие режимы, за исключением специальных случаев, должны исключаться системами управления. При рассмотрении кинематических связей особо следует остановиться на сопутствующих движениях, сопровождающих основноедвижение АТС. К ним относятся продольные, поперечные, вертикальные и угловые колебания АТС, возникающие как вследствие неровностей или изменения геометрических характеристик дорог (кинематические факторы), так и из-за неоднородности реакций несущего основания, управления или неравномерности действия нагрузок (силовые связи). Сопутствующие движения ухудшают, как правило, энергетику и управляемость A'TC, усложняют информационное обеспечение, вызывают дополнительные силовые знакопеременные нагрузки на узлы и системы АТС, что требует учета при управлении.
Силовые связи АТС с окружающей средой характеризуются продольными и поперечными силами, а также моментами, действующими на АТС. Из продольных сил наибольшее значение для движения АТС имеют сила тяги (Рк), силы сопротивления движению от грунта или покрытия (Рс), сила сопротивления воздуха (Рв), продольно-горизонтальная составляющая сил тяжести (PJ, продольные составляющие (Рп) поперечных и переменных сил центробежных, боковых сил сопротивления и т. д., продольные составляющие сил инерции (PJ. Уравнение тягового баланса АТС в каждый момент времени
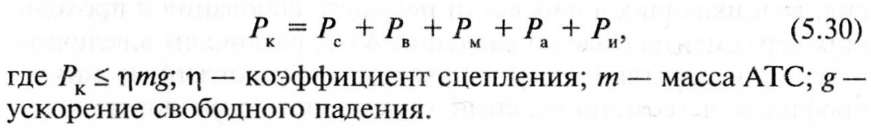
Данные
табл. 5.2 позволяют оценитьдиапазон
изменения результирующих воздействий
на АТС в управляемом движении:
![]()
При этом следует иметь в виду, что продольная составляющая сил тяжести и силы инерции могут быть направлены как по движению АТС, так и против него, что может привести к нарушению управляемости машины. Для поперечных сил справедливо аналогичное соотношение:
![]()
где Рu — поперечная составляющая центробежных сил; Ркб — поперечная составляющая тягового усилия (при повороте ведущих управляемых колес); Рсб — сопротивление боковомудвиже- нию АТС; Рм6 Риб — поперечные составляющие сил тяжести и сил инерции в вертикальной поперечной плоскости, проходящей через центр масс АТС; Рб — поперечные составляющие прочих сил, действующих на АТС.
Аналогично в управляемом движении, учитывая, чго боковая устойчивость и сцепление шин в поперечном направлении несколько меньше, чем в продольном:
![]()
Наряду с силами, направление действия которых сохраняется во время движения, на АТС действуют нагрузки, изменяющиеся не только по величине, но и по направлению. К их числу относятся ветровая нагрузка, а также силы, возникающие при сопутствующем движении АТС. Продольные и поперечные составляющие этих сил в выражении тягового баланса и уравнении равновесия в поперечной плоскости учитываются переменными Рn ,Рб.
Состав, величина и направление вектора моментов, действующих на АТС в процессе движения, определяются крутящим моментом на ведущих колесах, смещением линий действия сил, возникающих в плоскости несущего основания и проходящих через центры масс и давлений АТС, различием в величине и времени действия опорных реакций, обусловленных микропрофилем и геометрическими характеристиками дорог, изменением положения АТС, смещением вследствие этого центра давлений и появлением сил инерции.
В результате окружающая среда будет влиять на нашу систему в виде дополнительного момента сопротивления Mh, который является добавкой к основному моменту сопротивления Мг В общем виде момент, связанный с помехой, можно записать как
![]()
где Mh — величина момента, связанного с помехой; т — масса АТС; g- 9,81м/с2; а — угол наклона дороги; n — коэффициент сцепления с дорогой
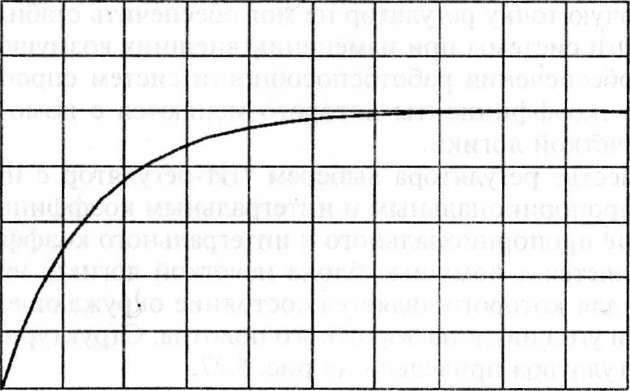
Как было отмечено, момент, связанный с помехой, является добавкой к основному моменту сопротивления движения АТС, и в результате момент сопротивления Mt примет вид, показанный на рис. 5.24
![]()
где Мк это момент сопротивления движения АТС без учета влияния окружающей среды.
В соответствии с этим будет изменяться и рабочая точка двигателя. Для поддержания заданной скорости при изменении Мк необходимо изменять и вращающий момент Ме.
Рассмотрим работу системы стабилизации при скорости движения 60 км/ч по дороге с коэффициентом сцепления, равным
Рис.
5.24. График момента, связанного с помехой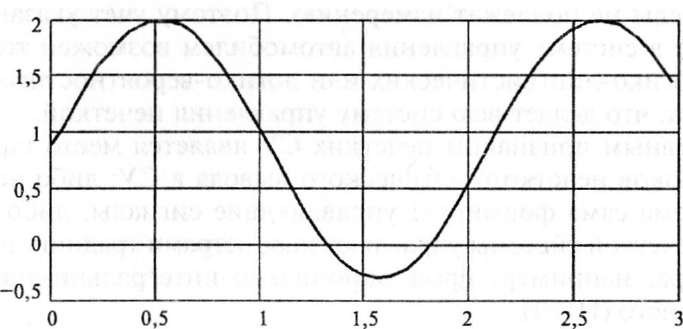
и переходный процесс в системе с регулятором, настроенным без учета помехи, будет как на рис. 5.25. Как видно из рисунка, желательна перенастройка регулятора.
После перенастройки на полученную передаточную функцию двигателя регулятор будет иметь следующую передаточную функцию:
![]()
В этом случае переходный процесс, как видно из рис. 5.26, становится удовлетворительным. Следовательно, при изменении коэффициента сцепления или угла наклона дорожного полотна меняется и момент сопротивления, приводящий к изменению передаточной функции объекта управления. Поэтому для поддержания заданного качества управления необходима перенастройка регулятора или его адаптация.
Таким образом, параметры регулятора необходимо подстраивать для каждого состояния окружающей среды и автомобиля, т. е. осуществлять адаптивное управление. Однако, в общем случае, коэффициент сцепления и ряд других параметров окружающей среды не подлежат измерению. Поэтому учет указанных факторов в системе управления автомобилем возможен только в виде логико-лингвистических или логико-вероятностных переменных, что делает всю систему управления нечеткой.
Основным признаком нечетких СУ является место нахождения блоков нечеткого логического вывода в СУ: либо нечеткая система сама формирует управляющие сигналы, либо сигналы с нечеткой системы управляют параметрами традиционного регулятора, например, пропорционально-интегрально-дифференциального (ПИД).
единице, и углом
наклона —10°. Дополнительный момент
будет равен 540 Нм.
Передаточная функция
двигателя в этом случае
Рис.
5.25. Переходный процесс в системе
стабилизации с настроенным ПИ-регулятором
для скорости движения 60 км/ч, при движении
по дороге с коэффициентом сцепления 1
и углом наклона 10°. Регулятор настроен
без учета помехи
Рис.
5.26. Переходный процесс в системе
стабилизации с настроенным ПИ-регулятором
для скорости движения 60 км/ч, при движении
по дороге с коэффициентом сцепления 1
и углом наклона 10°. Регулятор настроен
с учетом помехи![]()

автоматики до космических и оборонных систем. Нечеткие системы отличаются робастностыо, простотой разработки и реализации, низкой стоимостью. Однако экспертный опыт может быть использован далеко не для всех объектов. Поэтому существует тенденция к интеграции нечетких систем и систем имитационного моделирования с целью извлечения знаний о процессе управления сложным объектом. Это позволяет перейти от модели объекта к модели управления объектом.
Нечеткий логический регулятор (HJIP) может иметь несколько параметров, которые настраиваются для получения наилучшего качества регулирования, однако подавляющая часть информации, необходимой для управления, ему должна быть задана априори.
В рассмотренной ранее системе стабилизации автотранспортного средства по скорости есть существенный недостаток. Система стабилизации не может обеспечить должного качества регулирования на всем рабочем диапазоне. Для обеспечения качественной стабилизации параметры ПИ-регулятора должны меняться, в общем случае закон изменения коэффициентов регулятора неизвестен и положение рабочей точки в будущем также непредсказуемо. Это приводило к тому, что настроенный на одну рабочую точку регулятор не мог обеспечить стабилизацию по скорости системы при изменении внешних возмущений.
Для обеспечения работоспособности систем спроектируем регулятор, коэффициенты которого меняются с помощью аппарата нечеткой логики.
В качестве регулятора выберем ПИ-регулягор с изменяющимися пропорциональным и интегральным коэффициентами. Изменение пропорционального и интегрального коэффициента осуществляется с помощью блока нечеткой логики, входными данными для которого является состояние окружающей среды, скорость и угол наклона дорожного полотна. Структурная схема такого регулятора приведена на рис. 5.27.
Нечеткий регулятор состоит из ПИ-регулятора и двух нечетких блоков: блока, определяющего коэффициент сцепления с дорогой на основе данных о скорости и окружающей среды (1), и блока, определяющего значения коэффициентов ПИ-регулятора на основе данных о скорости, угле наклона дорожного полотна и возможном коэффициенте сцепления (2). Нечеткие блоки реализуют алгоритм нечеткого вывода Мамдани [16].
Рис.
5.27. Структурная схема нечеткого
регулятора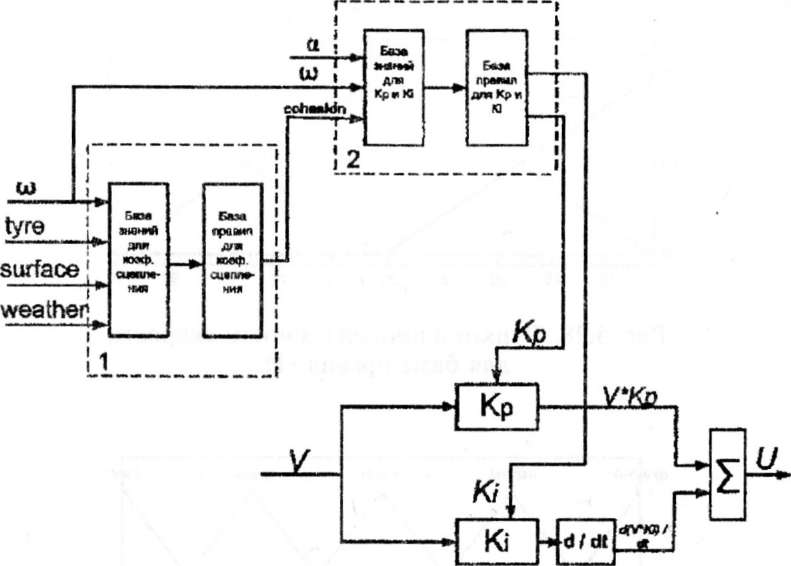
В Базу знаний блока (1) поступают данные о типе дорожного полотна (surface): земля, асфальт, гравий, трава, песок; данные о погодных условиях (weather): лед, снег, дождь, влажно, сухо; данные о типе и состоянии шин, установленных на АТС (tyre): стертые, летние, зимние; скорости движения АТС (ю): быстро, средне, медленно. После чего на основе поступивших значений определяется принадлежность этих значений соответствующим термам (см. рис. 5.28—5.30).
Скорость задается на участке со [0;55], единичными функциями принадлежности (рис. 5.28): низкая (low), средняя (medium), высокая (high).
Поверхность задается единичными функциями принадлежности на интервале [—1,1] (рис.5.29): земля (ground), асфальт (asphalt), гравий (gravel), трава (grass), песок (sand).
Погода задается единичными функциями принадлежности на интервале [—1,1] (рис. 5.30): лед (ice), снег (snow), дождь (rain), влажно (wet), сухо (dry).
Рис.
5.28. Функции принадлежности скорости
для базы правил (1)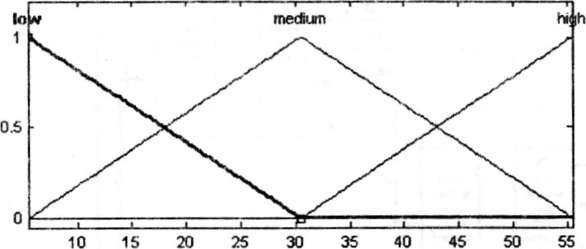
Рис.
5.29. Функции принадлежности состояния
поверхности для базы правил (1)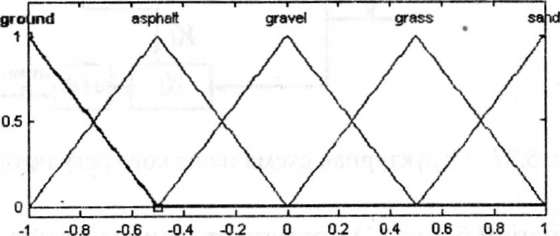
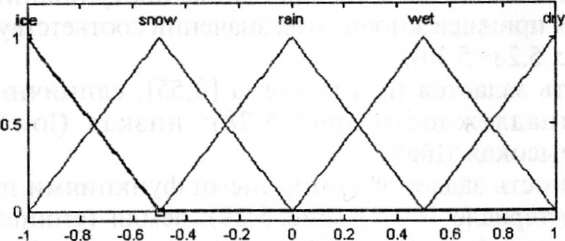
Рис. 5.30. Функции принадлежности погодных условий для базы правил (1)
Тип шин задается единичными функциями принадлежности на интервале [—1,1] (рис. 5.31): стертые (bald), летние (summer), зимние (snow tyre).
Рис.
5.31. Функции принадлежности типов шин
для базы правил (1)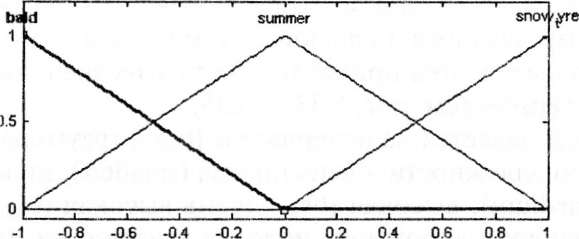
Далее термы передаются в Базу правил блока (1), в которой на основе правил нечеткого вывода определяется численное значение коэффициента сцепления.
Коэффициент сцепления задается непересекающимися треугольными функциями принадлежности на интервале [0,1]: самый малый (small), малый (smaller), средний (medium), большой (bigger), максимальный (max) (см. рис. 5.32).
Правила нечеткого вывода представляют собой выражения: если скорость (терм скорости), и погода (терм погоды), и поверхность (терм поверхности), и тип шин (терм типа шин), то коэффициент сцепления (значение коэффициента сцепления).
Рис.
5.32. Функции принадлежности значения
коэффициента сцепления в базе правил
(1)
В Базу знаний блока (2) поступают данные о скорости движения АТС (со): наименьшая, низкая, средняя, большая, самая большая; угле наклонадорожного полотна (а): большой отрицательный, маленький отрицательный, нулевой, маленький положительный, большой положительный; коэффициенте сцепления: малый, средний, большой. Затем на основе поступивших значений определяется принадлежность этих значений соответствующим термам (см. рис. 5.33 — 5.35).
Скорость задается на интервале со [0,55] треугольными функциями принадлежности: очень низкая (smallest), низкая (small), средняя (medium), высокая (big), очень высокая (biggest).
Угол наклона дорожного полотна задается на интервале а [—10,10], треугольными функциями принадлежности: большой отрицательный (smallest), маленький (small) отрицательный,
Рис.
5.33. Функции принадлежности скорости
для базы правил (2)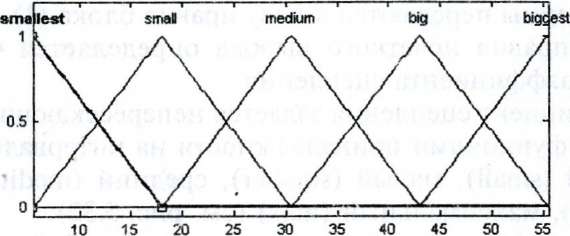
Рис.
5.34. Функции принадлежности угла наклона
дорожного полотна для базы правил (2)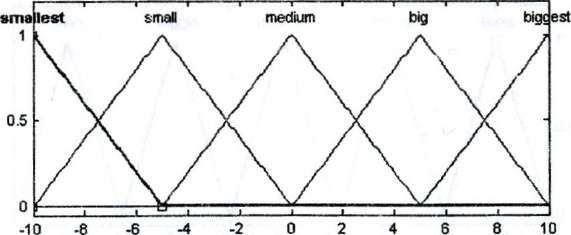
Рис.
5.35. Функции принадлежности коэффициента
сцепления с дорожным полотном для базы
правил (2)
нулевой (medium), маленький положительный (big), большой положительный (biggest).
Коэффициент сцепления задается на интервале 3 [0,1 ] треугольными функциями принадлежности: малый (small), средний (medium), большой (big).
Далее в Базе правил (2) на основе правил нечеткого вывода определяются численные значения коэффициентов Кр и Ki.
Пропорциональный коэффициент ПИ-регулятора Кр задается непересекающимися треугольными термами на интервале [1, 50]: самый малый (smallest), малый (small), средний (medium), большой (big), максимальный (biggest) (см. рис. 5.36).
Интегральный коэффициент ПИ-регулятора К.задается непересекающимися треугольными термами на интервале [1, 12]:
Рис.
5.36. Функции принадлежности пропорционального
коэффициента ПИ-регулятора в базе
правил (2)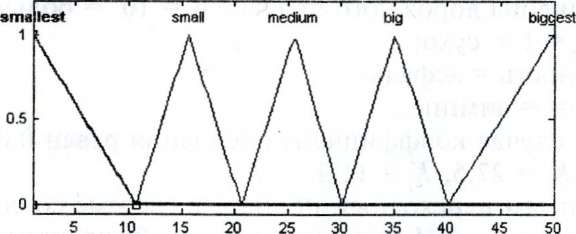
самый малый (smallest), малый (small), средний (medium), большой (big), максимальный (biggest) (см. рис. 5.37).
Правила нечеткого вывода представляют собой выражения: если скорость (терм скорости) и коэффициент сцепления (терм коэффициента сцепления) и угол наклона (терм угла наклона), то пропорциональный коэффициент ГШ-регулятора (значение пропорционального коэффициента) и интегральный коэффициент ПИ-регулятора (значение интегрального коэффициента).
Рис.
5.37. Функции принадлежности интегрального
коэффициента ПИ-регулятора в базе
правил (2.)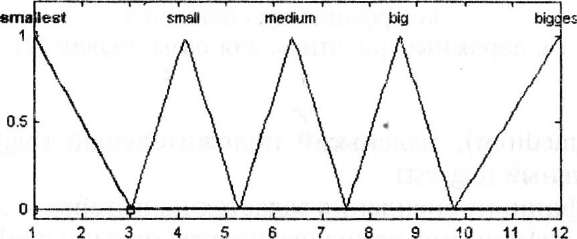
Рассмотрим работу системы с синтезированным нечетким ПИ- регулятором.
Структурная схема системы стабилизации остается прежней. Регулятор приведен на рис. 5.27.
Пусть система работает при следующих условиях: скорость ш = 33 l/c = средняя;
угол наклона дорожного полотна а = 10° = большой; погода = 1 = сухо;
поверхность = асфальт;
тип шин = зимние.
В этом случае коэффициент сцепления равен 0,86, а коэффициенты Кр = 27,5, К. = 11,2.
Рассмотрим переходный процесс в системе со спроектированным нечетким ПИ-регулятором (как было показано ранее в системе с обычным ПИ-регулятором невозможно обеспечить качественный переходный процесс), смоделировав ее в ППП Simlink (см. рис. 5.38).

При моделировании было:
fi — угол наклона дорожного полотна от —10 до 10;
w — скорость от 0 до 55 1/ с;
surface — тип поверхности (минус 1 — земля, минус 0,5 — снег, 0 — дождь, 0.5 — трава, 1 — песок);
weather — погода (минус 1 — лед, минус 0,5 — снег, 0 — дождь, 0,5 — влажно, 1 — сухо);
tyre — тип шин (минус 1 — стертые, 0 — летние, 1 — зимние);
in — задающее воздействие, равное 256;
PID controller — ПИ-регулятор;
DAC - ЦАП;
ADC - АЦП;
Engine — двигатель;
Cohesion — блок нечеткого регулятора, определяющий коэффициент сцепления;
PID — блок нечеткого ПИ-регулятора, определяющий значение пропорциональной и интегральной составляющей;
set К Т Mh — блок, определяющий по значению скорости, угла наклона и коэффициента сцепления, момент сопротивления движению и значения постоянных К и Т двигателя (функция setkt.m);
Блоки ЦАП и АЦП в ППП Simulink имеют структуру, показанную нарис. 5.18. Блок-схемадвигателя в ППП SimulinknoKa- зана на рис. 5.39.
Значения Kpart и Tpart задаются функцией setKT.m, значения пропорционального и интегрального коэффициента ПИ-
Рис.
5.39. Схемадвигателя в пакете прикладных
программ
Siniulink
регулятора задаются функцией setpi.m, тексты которых приведены ниже.
Функция setKT.m
function [sys, x0, str, ts] = setkt (t,x,w,flag) switch flag, case 0,
[sys, x0, str, ts] = mdlInitializeSizes; case 3,
sys = mdlOutputs(t,x,w); case {l,2,4,9} sys = []; otherwise
error(["Unhandled flag = ",num2str(flag)]); end
function [sys, x0, str, ts] = mdlInitializeSizes;
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 0;
sizes.NumInputs = 3;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [J;
str = [];
ts = [0 0];
function sys = mdlOutputs(t,x,M) fi = «(I); n u = u( 2); w = i/<3);
%дополнительный момент сопротивления mass = 2000; g= 10; rad = fi/57.3;
Mh = (nu*mass*g*cos(rad)+mass*g*sin(rad))/30; %параметры двигателя
dw = (55.5—5.5)/15;
dl = (2.5)/1000;
% считаем момент J
m = 20;
Л = 0,5;
J = m*(R^2);
% считаем Мк
b = 300;
kt = (M-b)/w
Mk_w=kt*(w+dw)+b;
dMk = abs(Mk_w-M);
% считаем M1
xL = M/964; xdL = xL + dl; Mxl = xdL*964; dMl = abs(Mxl - М);
K= ((dMl/dl)*(xL/w))/((dMk/dw)-(dMi/dw));
%
%теперь считаем T= J/(dMk/dw - dMl/dw) Т = J/((dMk/dw) - (dMl/dw));
%устанавливает параметры двигателя в его передаточную функцию
set_param("dynhandicap5/Engine/Kpart", 'Numerator', [num2str(K)]);
set_param("dynhandicap5/Engine/Tpart",'Numerator', [num2str(T)]); sys=[];
Функция setPI.m
function [sys, x0, str, ts] = setkt (t,x,u,flag)
switch flag,
case 0,
[sys, x0, str, ts] = mdlInitializeSizes;
case 3,
sys = mdlOutputs(t,x,u);
case {l,2,4,9}
sys = []; otherwise
error(["Unhandled flag = ",num2str(flag)]);
end
function [sys, x0, str, ts] = mdlInitializeSizes;
sizes = snnsizes; sizes.NumContStates = 0; sizes.NumDiscStates = 0; sizes.NumOutputs = 0; sizes.NumInputs = 2; sizes.DirFeedthrough = 1; sizes.NumSampleTimes = 1; sys = simsizes(sizes);
x0 = [];
str = [];
ts = [0 0];
function sys = mdlOutputs(t,x,u)
P = u(l);
I = u(2);
set_param("dynhandicap5/PID Controller",'P',[num2str(P)]); set_param("dynhandicap5/PID Controller",T,[num2str(I)j);
sys = [].
Полученный при моделировании переходный процесс показан на рис. 5.40.
Рис.
5.40. Переходный процесс в системе с
нечетким ПИ-регулятором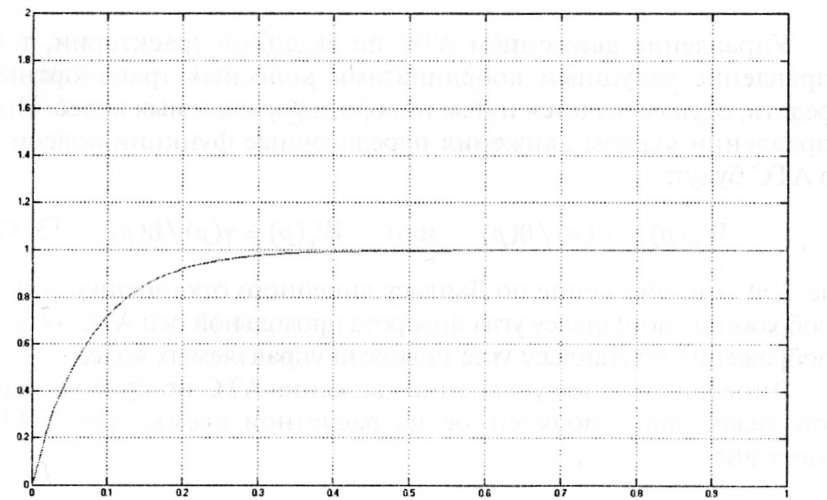
Как видно из рис. 5.40 процесс в системе удовлетворяет заданному условию при различных условиях работы. Следовательно, синтезированный нечеткий ПИ-регулятор обеспечивает требуемое качество работы. Тем не менее работа системы напрямую зависит от правил, разработанных экспертом. Отличительной особенностью системы является то, что ее модификация может быть очень просто проведена за счет изменения базы правил нечеткого вывода, перенастройки или структурного изменения системы при этом не потребуется.
Разработанная система стабилизации скорости движения представляет собой алгоритм в виде правил нечеткой логики и программный комплекс, позволяющий на их основе перенастраивать систему стабилизации. Эта система может быть легко интегрирована в общий контур управления и не требует переписывания программного кода. Данная особенность позволяет легко внедрить систему в кратчайшие сроки, без дополнительных временных и финансовых затрат на моделирование и разработку.
