Обработка результатов многократных измерений и проверка гипотезы о законе распределения

Цель работы - ознакомиться с методиками обработки многократных измерений и проверки гипотезы о нормальности распределения на основе критерия Пирсона.

Обработка результатов многократных измерений

При выполнении некоторых измерений существенную роль выполняет случайная погрешность, вызывающая рассеяние результатов измерений в серии многократных измерений.

Случайной погрешностью называется составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины.

Рассеяние результатов в ряду измерений - это несовпадение результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обусловленное действием случайных погрешностей.

Многократными измерениями называются измерения физической величины одного и того же размера, результаты которых получаются из нескольких следующих друг за другом измерений, т.е. состоящие из ряда однократных измерений.

Основным методом учета и частичного устранения влияния случайных погрешностей является получение избыточного числа измерений с последующей обработкой их специальными методами.

Построение гистограммы распределения

Для построения гистограммы статистического распределения результатов наблюдений, прежде всего необходимо произвести их группирование, то есть разделение ряда данных от наименьшего Х_мin до наибольшего Х_мах на r интервалов. Ширину интервала 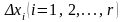выбирают постоянной для всего ряда данных, т.е.

.

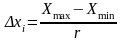Вычисленное значение ширины интервала обычно округляют. После этого подсчитывают числа 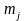, равные числу результатов, попадающих в каждый 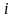‑ый интервал, то есть меньших или равных его правой и больших его левой границы. Отношения 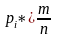, где n - общее число наблюдений или объем выборки, определяют частости и представляют собой статистические оценки вероятностей попадания результата наблюдений в ‑ый интервал. Если частость разделить на длину интервала Δx_i, то получим значение

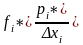
являющееся оценкой средней плотности распределения в интервале Δx_i. Отложив вдоль оси результатов наблюдений, как показано на рис. 3, интервалы Δx_i в порядке возрастания индекса i и построив на каждом интервале прямоугольник с высотой, равной f_i , получим график,  называемый гистограммой статистического распределения. При увеличении числа наблюдений число интервалов можно увеличить.

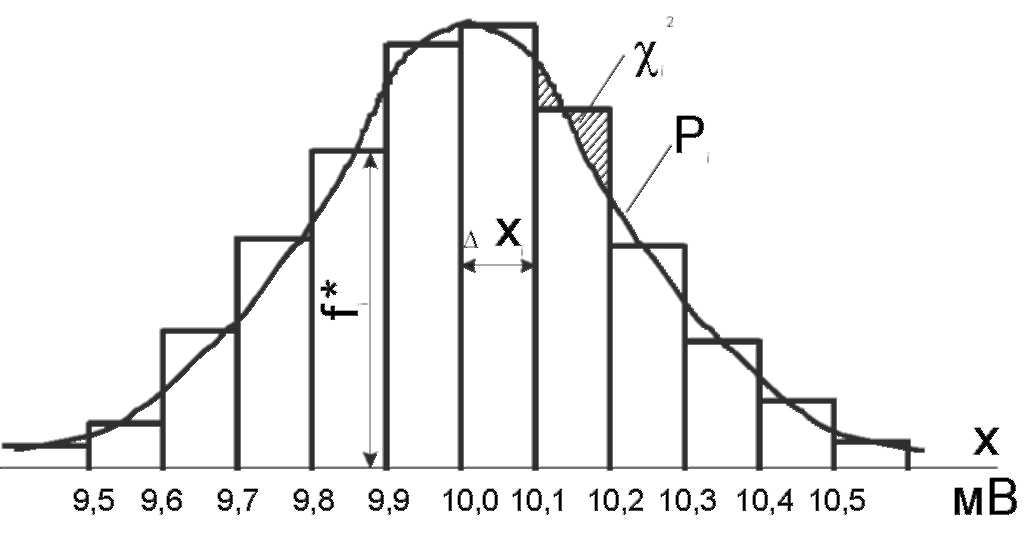
Рис. 3. Гистограмма нормального распределения случайных погрешностей

При этом сами интервалы уменьшаются, и гистограмма все больше приближается к плавной кривой, ограничивающей единичную площадь, - к графику плотности распределения результатов наблюдения.

При построении гистограмм рекомендуется пользоваться следующими правилами:

1. Число r интервалов выбирается в зависимости от числа наблюдений n согласно рекомендациям, приведенным в табл. 1.

Таблица 1. Рекомендованное число интервалов

N	r
10-100	7-9
100 - 500	8-12
500-1000	10-16
1000-10000	12-22

Длины интервалов удобнее выбирать одинаковыми. Однако если распределение крайне неравномерно, то в области максимальной концентрации результатов наблюдений следует выбрать более узкие интервалы.

Нормальное распределение случайных погрешностей возникает то­гда, когда на результат измерения действует множество случайных воз­мущений, ни одно из которых не является преобладающим.

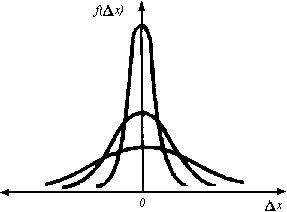
Рис. 4. Кривые нормального распределения случайных погрешностей

Кривая нормального распределения погрешностей симметрична относительно оси ординат. Это означает, что погрешности, одинаковые по величине, но противоположные по знаку, имеют одинаковую плотность вероятностей, т.е. при большом числе наблюдений встречаются одинаково часто. Математическое ожидание случайной погрешности равно нулю.

Из характера кривой следует, что при нормальном законе распреде­ления малые погрешности будут встречаться чаще, чем большие.

На рис. 4 изображены кривые нормального распределения с различными средними квадратическими отклонениями, причем σ₁ > σ₂ > σ₃.

Квантильная оценка погрешности представляется интервалом, на котором с заданной вероятностью 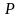встречаются 100% всех возможных значений случайной погрешности. Интервал с границами 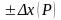называется доверительным интервалом случайной погрешности, а соответствующая ему вероятность - доверительной вероятностью. Принято границы доверительного интервала (доверительные границы) указывать симметричными относительно результата измерения. 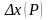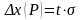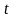Доверительные границы случайной погрешности , соответст­вующие доверительной вероятности , находят по формуле: , где - коэффициент, зависящий от и формы закона распределения.