§ 1.3 Естественная система координат

Во многих кинематических задачах траектория материальной точки известна заранее. В этом случае для описания движения можно применить «естественный» способ. Положение движущейся точки А определяют дуговой координатой l, которая равна расстоянию, пройденному точкой вдоль траектории от выбранного начала отсчета О (см. рис. 1.4). Таким образом, движение материальной точки будет полностью определено, если известны ее траектория, начало отсчета О, положительное направление отсчета дуговой координаты l и уравнение движения точки, т.е. зависимость l(t).

Рис. 1.4

Введем единичный вектор , направленный по касательной к траектории в сторону возрастания дуговой координаты l, как показано на рисунке. 1.4. Вектор скорости материальной точки также направлен по касательной к траектории, следовательно, его можно представить как

, (1.17)

где величина скорости v согласно (1.8) равна

. (1.18)

Продифференцировав обе части равенства (1.17) по времени, найдем ускорение материальной точки:

. (1.19)

Преобразуем последний член полученного выражения:

. (1.20)

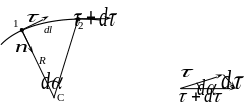
Рис. 1.5 а Рис. 1.5 б

Малый отрезок траектории dl совпадает с дугой окружности радиусом R с центром в некоторой точке С (см. рис. 1.5 а). Точку С называют центром кривизны траектории в данной точке, а радиус R – радиусом кривизны траектории в этой же точке.

Определим приращение вектора на участке траектории dl (см. рис. 1.5 а). Пусть , тогда . Из рисунка 1.5 б видно, что , , следовательно . При бесконечном уменьшении dl угол d также будет стремиться к нулю, и вектор окажется перпендикулярен вектору (т.к. при d0 два других угла в треугольнике на рис. 1.5 б стремятся к 90⁰). Таким образом, вектор будет направлен по нормали к траектории. Введем единичный вектор нормали к траектории в точке 1, направленный к центру кривизны О. Тогда

. (1.21)

С учетом (1.20) и (1.21) выражение (1.19) для ускорения материальной точки примет вид

. (1.22)

Первое слагаемое в выражении (1.22) называется тангенциальным (или касательным) ускорением , второе слагаемое называется нормальным ускорением :

, . (1.23)

Ускорение материальной точки в естественной системе координат часто называют полным ускорением. Очевидно, что

, (1.24)

. (1.25)

Интересно отметить, что величина тангенциального ускорения обусловлена изменением величины скорости материальной точки и не зависит от конкретной формы траектории. Поскольку и , то, исключив , получим . Следовательно, если величина скорости v возрастает, то и вектор сонаправлен вектору скорости , если же v уменьшается, то и вектор тангенциального ускорения будет направлен противоположно вектору скорости.

Появление нормального ускорения связано с изменением направления вектора скорости при движении материальной точки по криволинейной траектории. При движении точки с постоянной по величине скоростью и . Одним из примеров такого движения является равномерное движение по окружности, когда ¹.

При движении точки по прямой R    и .

Рис. 1.6 а Рис. 1.6 б

Примеры взаимной ориентации векторов , и показаны на рисунке 1.6 (на рис. 1.6 а модуль скорости материальной точки увеличивается, а на рис. 1.6 б – уменьшается).

Разберем задачу на определение параметров траектории с использованием тангенциального и нормального ускорений.

Задача 1.3. Уравнение движения материальной точки имеет вид , где ,  и  - постоянные величины. Найти зависимость радиуса кривизны R траектории точки от времени t.

Решение.

Согласно (1.23) и (1.25) радиус кривизны траектории точки можно выразить как

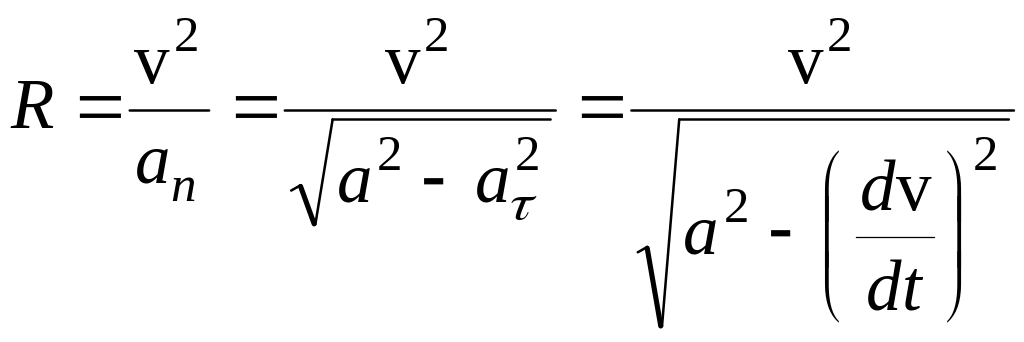. (1.26)

Найдем зависимости v и а от времени. Из условия задачи следует, что скалярные уравнения движения точки имеют вид , и , отсюда

, , ;

; (1.27)

; (1.28)

, , ;

. (1.29)

Подставив выражения (1.27), (1.28) и (1.29) в (1.26), получим искомую зависимость радиуса кривизны траектории от времени:

.

Лекция 2. Кинематика абсолютно твердого тела