§ 5.2. Закон Гука

Для описания процесса деформирования тела принято использовать понятия абсолютной и относительной деформации. Пусть x – какая-либо величина, характеризующая форму или размеры тела. Абсолютной деформацией называется изменение х величины х, а относительной деформацией - отношение абсолютной деформации к значению величины х в недеформированном состоянии: .

В 1660 г. Р. Гук¹ установил, что при упругих деформациях напряжение тела прямо пропорционально его относительной деформации (закон Гука):

, (5.2)

где - модуль упругости. Величина К_х определяется свойствами материала тела и конкретным типом деформации. Эксперименты показали, что закон Гука выполняется лишь в определенном диапазоне напряжений в пределах от нуля до некоторого максимального значения, получившего название предела пропорциональности _п.

Рис. 5.2

Любую деформацию твердого тела можно представить как комбинацию двух простейших видов деформации – одностороннего растяжения (или сжатия) и сдвига. В качестве примера одностороннего растяжения рассмотрим продольное растяжение однородного стержня. Возьмем стержень, имеющий в недеформированном состоянии длину l и площадь поперечного сечения S. Один конец стержня закрепим, а к другому приложим силу , как показано на рисунке 5.2. Стержень будет удлиняться до тех пор, пока возникшая в нем сила упругости не станет равной по величине деформирующей силе . При этом стержень удлинится на и в нем возникнет напряжение . Величиной, характеризующей размер тела (стержня), в данном случае является его длина ( ). Следовательно, абсолютная деформация . Модуль упругости К_l для одностороннего растяжения или сжатия называется модулем Юнга² Е. Таким образом, закон Гука (5.2), описывающий продольную деформацию стержня, будет иметь вид

. (5.3)

Значения модуля Юнга для некоторых материалов приведены в таблице 5.1.

Таблица 5.1

Материал	Модуль Юнга Е, 107 Па	Коэффициент Пуассона 	Модуль сдвига G, 107 Па
Алюминий	7000	0,31	2600
Железо	19600	0,28	8100
Сталь	19600	0,25	8100
Свинец	1600	0,446	560

Задача 5.1. Какой наибольший груз может выдержать стальная проволока диаметром мм, не выходя за предел пропорциональности МПа. Чему будет равно при этом относительное удлинение проволоки ?

Решение

На груз, закрепленный на проволоке, действуют сила тяжести и сила упругости (см. рис. 5.3).

Рис. 5.3

Поскольку груз находится в равновесии, то . С другой стороны, , где площадь поперечного сечения проводника . Находим массу груза, соответствующую пределу пропорциональности материала проволоки:

кг.

Соответствующее данной массе груза относительное удлинение проволоки найдем из закона Гука (5.3). Модуль Юнга стали возьмем из таблицы 5.1: Па. Имеем:

.

Таким образом, область применимости закона Гука для стали ограничена очень малыми относительными деформациями: (или 0,15%).

Растяжение (сжатие) тел сопровождается сужением (расширением) площади их поперечного сечения. Отношение относительного поперечного сужения тела к его относительному продольному удлинению называется коэффициентом Пуассона¹ :

, (5.4)

где d – поперечный размер тела, d – его изменение. Значения коэффициента Пуассона для некоторых материалов приведены в таблице 5.1.

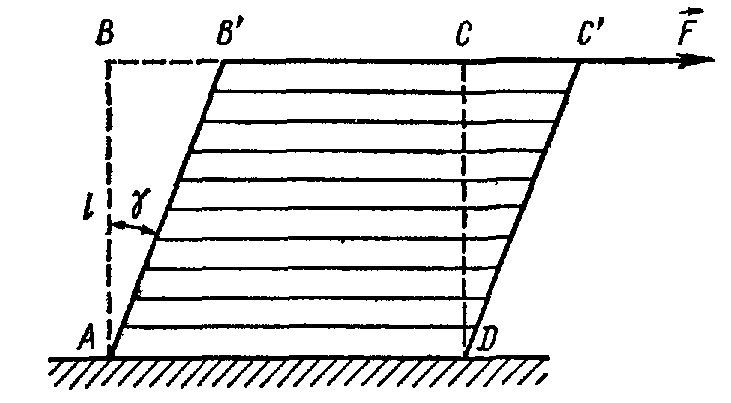
Рис. 5.4

Сдвигом называется деформация, при которой все слои твердого тела, параллельные некоторой плоскости, называемой плоскостью сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (см. рис. 5.4.). На рисунке показано продольное сечение бруска, испытывающего деформацию сдвига. Грань AD бруска закреплена. Сдвиг происходит под действием касательной силы , приложенной к грани BC. Величина называется абсолютным сдвигом, а - относительным сдвигом. Угол  называется углом сдвига. При малом сдвиге и . В результате сдвига в бруске возникает касательная сила упругости и появляется касательное напряжение , где S – площадь грани ВС. Модуль упругости, соответствующий деформации сдвига, называется модулем сдвига G. Закон Гука в данном случае имеет вид

. (5.5)

Модули сдвига некоторых материалов приведены в таблице 5.1.

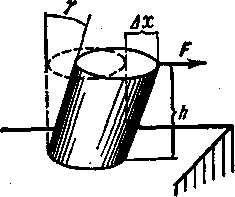Рис. 5.5

Задача 5.2. Нижнее основание железной тумбы, имеющей форму цилиндра диаметром см и высотой см, закреплено неподвижно. На верхнее основание тумбы действует сила кН, как показано на рисунке 5.5. Определить: 1) тангенциальное напряжение в материале тумбы; 2) угол сдвига тумбы ; 3) смещение верхнего основания тумбы.

Решение

Площадь поперечного сечения тумбы . Тангенциальное напряжение в материале тумбы (МПа).

Взяв модуль сдвига железа Па из таблицы 5.1, при помощи закона Гука (5.5) находим угол сдвига: (рад).

Из рисунка 5.5 видно, что смещение верхнего основания тумбы можно найти как (мкм).