§3.4. Теплоемкость

Для количественного описания тепловых свойств макроскопических тел в термодинамике используется понятие теплоемкости. Теплоемкостью тела С называется отношение переданного ему малого количества теплоты к изменению температуры тела :

. (3.14)

В системе СИ теплоемкость измеряется в джоулях, деленных на кельвин (Дж/К).

Помимо теплоемкости используют также понятия удельной теплоемкости и молярной теплоемкости с. По определению

, (3.15)

, (3.16)

где m – масса тела,  - количество вещества. Удельная теплоемкость измеряется в джоулях, деленных на килограмм и на кельвин (Дж/(кгК)), молярная – в джоулях, деленных на моль и на кельвин (Дж/(мольК)). Из формул (3.14) – (3.16) следует, что

и , (3.17)

где М – молярная масса.

Теплоемкость зависит от вида процесса, происходящего в макроскопической системе. Найдем молярную теплоемкость идеального газа в изохорном с_V и изобарном c_p процессах.

Изохорный процесс

Воспользуемся определением молярной теплоемкости (3.16) и формулой (3.13). Имеем:

,

. (3.18)

Выражение (3.18) позволяет записать внутреннюю энергию идеального газа в виде

. (3.19)

Изобарный процесс

Используем формулу (3.13):

,

. (3.20)

Таким образом, с_V и с_р не зависят ни от состояния газа, ни от его молярной массы, а определяются только числом степеней свободы молекул. Кроме того, для любого идеального газа

. (3.21)

Равенство (3.21) носит название уравнения (или теоремы) Майера.

Задача 3.3. Определите удельную теплоемкость смеси водорода и гелия с_уд при постоянном объеме, если количества вещества обоих газов в смеси одинаковы и равны .

Решение

Согласно (3.17) удельная теплоемкость смеси , где масса смеси (молярная масса водорода кг/моль, гелия кг/моль).

Из определения теплоемкости (3.14) следует, что она является аддитивной величиной. Иными словами, теплоемкость смеси газов равна сумме теплоемкостей этих газов, взятых по отдельности. Имеем:

где число степеней свободы водорода , гелия .

Окончательно находим:

.

§3.5. Адиабатный процесс

Адиабатным (или адиабатическим) называется процесс, происходящий без теплообмена с окружающей средой ( ). На практике адиабатный процесс можно осуществить при достаточно быстром расширении или сжатии газа, т.е. когда процесс протекает настолько быстро, что теплообмен между газом и окружающей средой не успевает произойти.

Получим уравнение состояния идеального газа, описывающее адиабатный процесс. Из первого закона термодинамики (3.10) следует, что в адиабатном процессе выполняется условие . Используя формулы (3.4) и (3.19) это условие для идеального газа можно переписать в виде

.

Из уравнения Менделеева-Клапейрона находим:

; ;

. (3.22)

Учтем, что , и введем безразмерную величину , называемую показателем адиабаты. Отметим, что показатель адиабаты идеального газа определяется только числом степеней свободы его молекул. Действительно, согласно (3.18) и (3.20),

. (3.23)

Преобразуем и проинтегрируем уравнение (3.22):

; ; ;

. (3.24)

Уравнение (3.24) и есть искомое уравнение состояния идеального газа в адиабатном процессе или уравнение Пуассона. Воспользовавшись уравнением Менделеева-Клапейрона, уравнение Пуассона легко записать в других переменных:

и . (3.25)

Получите выражения (3.25) самостоятельно.

График адиабатного процесса или адиабата в координатах (p,V) идет круче изотермы, уравнение которой имеет вид (см. рис. 3.4). Это объясняется тем, что показатель адиабаты .

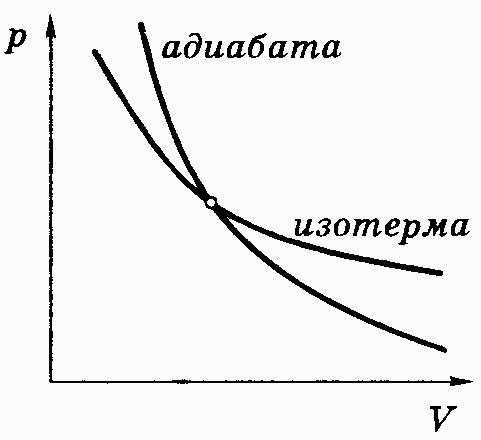
Рис. 3.4

Задача 3.4. При адиабатном расширении кислорода с начальной температурой К его внутренняя энергия уменьшилась на кДж, а объем увеличился в раз. Определите массу кислорода m.

Решение

Молекула кислорода О₂ состоит из двух атомов, следовательно, число степеней свободы кислорода . По формуле (3.23) определим показатель адиабаты кислорода: . Конечную температуру кислорода найдем из второго уравнения (3.25):

.

Согласно (3.3) изменение внутренней энергии газа равно

,

где кг/моль – молярная масса кислорода.

Находим массу газа:

г.

Изотермический, изобарный, изохорный и адиабатный процессы являются представителями более широкого класса политропных процессов. Политропными (или политропическими) называются процессы, уравнения которых в координатах (р,V) имеют вид

, (3.26)

где n – произвольное число, называемое показателем политропы. Показатель политропы может быть как положительным, так и отрицательным. В ходе любого политропного процесса теплоемкость газа остается постоянной, т.е. . Показатель политропы n может быть выражен через c_V, c_p и с_n:

. (3.27)

Из формулы (3.27) следует, что показатель политропы для изотермического процесса ( ) равен n = 1, для адиабатного ( ) , для изохорного ( ) , для изобарного ( ) .

Задача 3.5. В ходе некоторого политропного процесса объем кислорода был увеличен в раза, давление при этом уменьшилось в раз. Определите молярную теплоемкость кислорода в этом процессе.

Решение

Из уравнения политропы следует (3.26) следует, что давление и объем газа в начальном состоянии 1 и конечном состоянии 2 связаны между собой соотношением , отсюда

.

Молярную теплоемкость газа в политропном процессе выразим из формулы (3.27):

.

Учтем, что молекула кислорода О₂ – двухатомная, и ее число степеней свободы . Имеем:

, ;

(Дж/К).

Лекция 4. Второй закон термодинамики. Энтропия