§2.3. Распределение молекул газа по кинетическим энергиям
Используя функцию
распределения (2.9) молекул по скоростям,
можно получить их распределение по
значениям кинетической энергии
поступательного движения
.
Пусть у нас имеется
N
молекул газа. Обозначим dN
число молекул, скорости которых лежат
в интервале
,
а кинетические энергии – в интервале
.
Согласно определению функции распределения
имеем:
. (2.15)
Учитывая, что
,
и используя формулу (2.9), из выражения
(2.15) получим:
. (2.16)
График функции
показан
на рисунке 2.6. Наиболее вероятная
кинетическая энергия поступательного
движения молекул находится из условия
и равна
.
Рис. 2.6
§2.4. Распределение молекул газа по потенциальным
энергиям
До сих пор мы предполагали, что на молекулы газа не действуют внешние силы, поэтому при выводе основного уравнения МКТ идеального газа (1.7) молекулы считались равномерно распределенными по объему сосуда. На самом же деле молекулы любого газа всегда находятся в поле тяготения Земли. Если бы не было силы тяжести, атмосферный воздух вследствие хаотического теплового движения молекул рассеялся бы в космосе. Если бы не было теплового движения молекул, они бы упали на поверхность Земли. В реальности же тяготение к Земле и тепловое движение приводят газ к такому равновесному состоянию, когда его концентрация и давление убывают с высотой.
Найдем зависимость
давления газа р
от высоты h.
Газ будем считать идеальным, а его
температуру – одинаковой на всех высотах
(
).
Давление на нулевой высоте (на поверхности
Земли) обозначим p0.
Выделим мысленно малый объем газа dV,
находящийся на высоте h
и имеющий форму цилиндра с площадью
основания S
и малой высотой dh
(см. рис. 2.7).
Рис. 2.7
Условие равновесия выделенного объема газа имеет вид
,
где силы, действующие
на нижнее и верхнее основания цилиндра
со стороны окружающего газа равны,
соответственно,
и
(p
– давление газа на высоте h,
- на высоте
;
масса газа в цилиндре
(
- плотность газа на высоте h).
Имеем:
;
.
Связь между
плотностью газа и его давлением найдем
из уравнения Менделеева-Клапейрона
(1.9):
,
где М
- молярная масса газа. Тогда
,
,
,
. (2.17)
Выражение (2.17) называется барометрической формулой. Барометрическая формула позволяет определять высоту h при помощи барометра. Барометр, проградуированный для измерения высоты над уровнем моря, называется альтиметром.
Задача 2.2. Идеальный газ с молярной массой М находится в высоком вертикальном цилиндрическом сосуде с площадью основания S и высотой Н. Температура газа Т, его давление на нижнее основание цилиндра p0. Считая, что температура и ускорение свободного падения g не зависят от высоты, найти массу газа в сосуде.
Рис. 2.8
Решение
Мысленно разобьем сосуд на цилиндры малой высоты dh (см. рис. 2.8). В пределах каждого такого цилиндра давление газа можно считать одинаковым. Найдем массу газа dm в цилиндре, находящемся на высоте h, для чего воспользуемся уравнением Менделеева-Клапейрона (1.9) и барометрической формулой (2.17). Имеем:
.
Общую массу газа в сосуде найдем, проинтегрировав полученное выражение по h в пределах от 0 до Н:
.
Воспользовавшись
основным уравнением МКТ идеального
газа
из формулы (2.17) можно получить зависимость
концентрации молекул газа от высоты и
потенциальной энергии молекулы EP.
Обозначим n0
концентрацию на нулевой высоте. Имеем:
,
. (2.18)
Формула (2.18) называется распределением молекул газа по потенциальным энергиям или распределением Больцмана.
Справедливость распределения Больцмана была в 1909 году подтверждена экспериментально французским физиком Ж. Перреном1, который исследовал под микроскопом распределение мельчайших частиц эмульсии смолы гуммигута в воде. Результаты эксперимента совпали с расчетами, выполненными с использованием формулы (2.18).
В заключение
отметим, что распределения Максвелла
и Больцмана можно объединить в одно
общее распределение Максвелла-Больцмана,
согласно которому число молекул dN,
проекции скорости и координаты которых
лежат в интервале
,
,
,
,
,
,
можно найти как
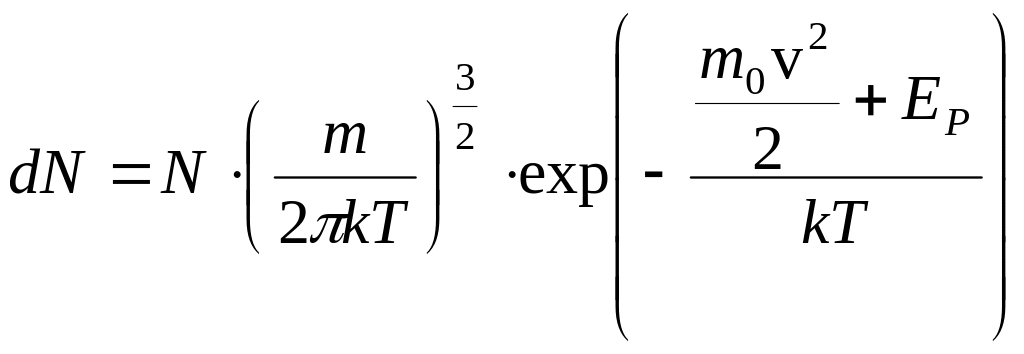, (2.19)
где
,
- потенциальная энергия молекулы в точке
с координатами
.
Лекция 3. Первый закон термодинамики