§ 2.1. Элементарные сведения из теории вероятностей

Статистической физикой называют раздел физики, в котором изучаются свойства макроскопических систем, исходя из индивидуальных свойств, составляющих систему микрочастиц (например, молекул).

Любое макроскопическое тело состоит из очень большого числа молекул (10¹⁵ и больше), поэтому описать движение каждой молекулы невозможно, да и не имеет смысла. Вместо рассмотрения движения каждой микрочастицы в отдельности статистическая физика оперирует средними значениями параметров частиц и устанавливает закономерности, связывающие усредненные характеристики микрочастиц со свойствами макросистемы в целом.

В основе статистической физики лежит теория вероятностей. Вероятность какого-либо события характеризуется кратностью его повторения. Если в N случаях i-событие происходит N_i раз, то вероятностью W_i этого события называется величина

.

Например, вероятность того, что подброшенная монета упадет «орлом» равна ½, «решеткой» - также ½. В молекулярной физике N – конечное, но, как правило, очень большое число, поэтому можно считать, что

. (2.1)

Вероятность того, что подброшенная монета упадет или «орлом» или «решеткой» составляет ½ + ½ = 1. Таким образом, сумма вероятностей всех возможных событий равна единице:

. (2.2)

Рассмотрим две основные теоремы теории вероятностей.

Теорема о сложении вероятностей: вероятность того, что произойдет одно из нескольких независимых друг от друга событий, равна сумме вероятностей этих событий. Например, если Вы бросаете игральный кубик, вероятность того, что в результате N бросаний выпадет число i или число k, равна

W_{i или k} = W_i + W_k. (2.3)

Теорема об умножении вероятностей: вероятность того, что произойдут несколько независимых друг от друга событий, равна произведению вероятностей этих событий. Например, вероятность того, что при N бросаниях двух кубиков на первом выпадет i и на втором выпадет k, равна

W_{i и k} = (N_i/N)(N_k/N) = W_i W_k. (2.4)

Задача 2.1. Определить вероятность W того, что при броске двух кубиков в сумме наберется 3 очка.

Решение

Три очка в сумме на двух кубиках может получиться в результате двух комбинаций: «1» на первом, «2» на втором и «2» на первом, «1» на втором. Обозначим вероятность этих комбинаций W_{1 и 2} и W_{2 и 1}. Согласно теореме о сложении вероятностей (2.3) искомая вероятность W = = W_{1 и 2} + W_{2 и 1} = 2 W_{1 и 2}. Вероятность выпадения какого-либо числа на кубике равна 1/6 (поскольку всего возможных событий 6, все они равновероятны, и их сумма, согласно (2.2), равна единице). По теореме об умножении вероятностей (2.4) находим W_{1 и 2} = 1/36. Вероятность того, что на двух кубиках в сумме выпадет три очка, равна W = 2/36 (5,6 %).

Среднее значение дискретной величины x можно найти, зная вероятности появления ее значений:

.

Рассмотрим случай, когда величина x является непрерывной (например, скорость молекул) и может случайным образом принимать значения из некоторой области (х₁, x₂). Разобьем всю область изменения величины x на малые интервалы х. Пусть нам известна вероятность W_x попадания величины х на интервал х. Зависимость

(2.5)

называется функцией распределения величины х. Функция f(x) имеет смысл плотности вероятности, т.е. численно равна вероятности того, что рассматриваемая величина окажется в единичном интервале вблизи значения x.

Один из возможных видов функции распределения изображен на рисунке 2.1. Из определения (2.5) следует, что вероятность обнаружения случайной величины в пределах интервала равна площади заштрихованной полоски шириной dx, показанной на рисунке.

Рис. 2.1

В ероятность попадания величины x в конечный интервал (a,b) равна

. (2.6)

Вероятность того, что случайная величина x примет какое-либо значения из своей области изменения, равна 1. Следовательно, интеграл от функции распределения, взятый по всей области (х₁, x₂), равен единице:

. (2.7)

Выражение (2.7) называется условием нормировки функции распределения, а интеграл, стоящий в его левой части – нормировочным интегралом. Из условия нормировки следует, что площадь под графиком f(x) всегда равна единице.

Зная функцию распределения f(x), можно найти средние значения x и произвольной функции g(x):

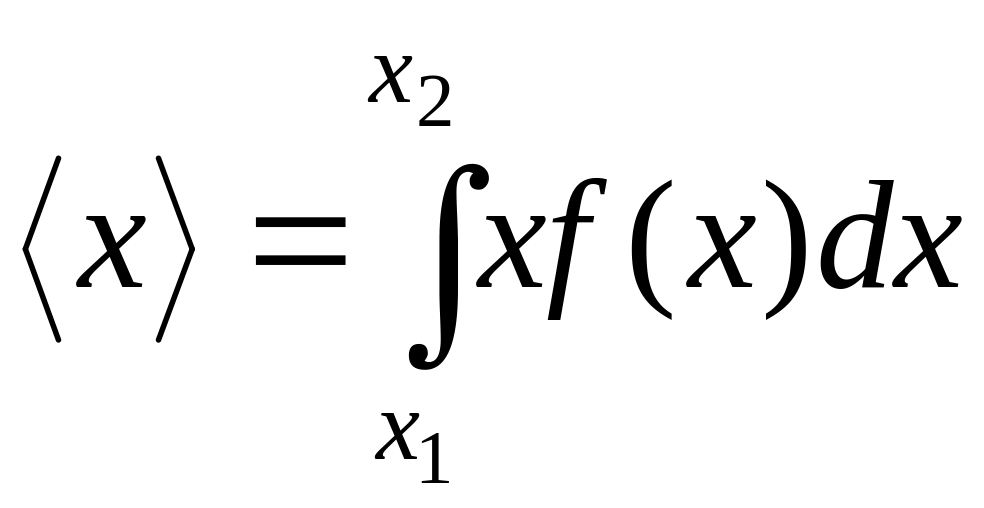и 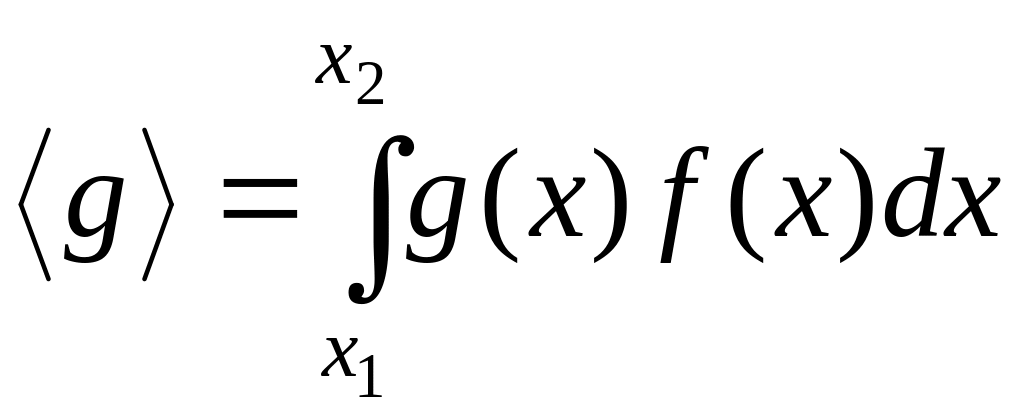. (2.8)