§ 6.1. Длина свободного пробега молекул

В лекции 15, посвященной второму закону термодинамики, было показано, что термодинамическому равновесию замкнутой макросистемы соответствует состояние с максимальной энтропией. Равновесное состояние является самым неупорядоченным. Оно характеризуется равномерным распределением молекул по объему системы и отсутствием макроскопических областей, в пределах которых температура, концентрация молекул, скорость движения вещества и другие макроскопические параметры заметно отличались бы от средних значений по системе в целом. В случае возникновения таких областей система стремится вернуться в равновесное состояние.

Процессы, в результате которых система возвращается к состоянию равновесия, приводят к увеличению энтропии и, следовательно, являются неравновесными. Эти процессы сопровождаются возникновением потоков или молекул, или теплоты, или импульса, или иных физических величин, по причине чего называются явлениями переноса. В настоящей лекции мы рассмотрим три явления переноса: диффузию (перенос массы), теплопроводность (перенос теплоты) и вязкое трение (перенос импульса).

Законы, описывающие явления переноса, рассмотрим на примере самой простой макросистемы – идеального газа. Переход идеального газа к равновесному состоянию обусловлен хаотическим тепловым движением его молекул. Очевидно, что чем быстрее движутся молекулы и чем дальше они могут удалиться от точки своего начального местонахождения за единицу времени, тем быстрее будет восстановлено равновесие в системе. В этой связи важную роль в количественном описании явлений переноса играет величина, называемая средней длиной свободного пробега молекулы.

Средняя длина свободного пробела молекулы - это среднее расстояние, которое проходит молекула газа между двумя последовательными столкновениями с другими молекулами. За одну секунду молекула в среднем проходит путь, численно равный средней арифметической скорости ее движения и испытывает соударений с другими молекулами. Очевидно, что

. (6.1)

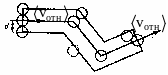
Рис. 6.1

Определим среднее число соударений , испытываемое за 1 с молекулой идеального газа при условии, что концентрация молекул равна n, их средняя арифметическая скорость , эффективный диаметр d. Сделаем мысленно «мгновенную фотографию» молекул газа и рассмотрим движение одной из них, полагая остальные молекулы неподвижными. Можно показать, что средняя относительная скорость одной молекулы относительно других молекул равна . Наша избранная молекула будет двигаться по ломанной линии, соударяясь со всеми неподвижными молекулами, центры которых окажутся внутри ломанного цилиндра диаметром 2d (см. рис. 6.1). Число таких молекул можно найти как произведение n на объем криволинейного цилиндра, равный . Итак,

, (6.2)

. (6.3)

Задача 6.1. Определите среднее число столкновений и среднюю длину свободного пробега молекул кислорода в нормальных условиях.

Решение

Найдем концентрацию молекул кислорода n из основного уравнения МКТ идеального газа:

(м^-3).

Среднюю скорость молекул кислорода можно найти по формуле (2.12):

(м/с).

Среднее число столкновений и среднюю длину свободного пробега найдем по формулам (6.2) и (6.3), соответственно. Эффективный диаметр молекулы О₂ возьмем из таблицы 5.1 (0,35 нм). Имеем:

(с^-1);

(м).

Отметим, что средняя длина свободного пробега молекулы кислорода при нормальных условиях превышает ее эффективный диаметр приблизительно в 200 раз.