§ 5.1. Уравнение состояния реального газа

До сих пор, говоря о газе, мы подразумевали идеальный газ, состояние которого описывается уравнением Менделеева-Клапейрона , где - молярный объем. Однако, опыт показывает, что данное уравнение далеко не всегда точно описывает свойства реальных газов. На деле , причем отличие величины , называемой коэффициентом сжимаемости газа, от единицы возрастает с увеличением давления газа (при неизменной температуре). Например, при давлении Па (или 1000 атмосфер¹) . Иначе говоря, чем выше давление газа, тем хуже он сжимается.

Существуют две причины того, что модель идеального газа плохо описывает свойства реальных газов при высоких давлениях. Во-первых, в модели идеального газа предполагается, что собственный объем молекул много меньше объема сосуда, занимаемого газом. Это предположение можно считать верным при нормальных условиях, когда объем молекул составляет менее 0,1% объема сосуда, однако при давлении 100 атм сами молекулы занимают уже примерно 70% объема сосуда!

Во-вторых, в модели идеального газа считается, что молекулы не взаимодействуют друг с другом на расстоянии. Эксперименты показывают, что это условие хорошо выполняется, когда расстояние между центрами молекул превышает 10^-9 м, что соответствует концентрации молекул порядка 10²⁷ м^-3. При бóльших концентрациях пренебрегать силами межмолекулярного взаимодействия нельзя. В действительности взаимодействие между молекулами носит сложный характер – на малых расстояниях ( 10^-10 м) они отталкиваются, на бóльших – притягиваются. Характерная зависимость Энергии взаимодействия U_вз между двумя молекулами от расстояния r между их центрами показана на рисунке 5.1. При молекулы отталкиваются, при - притягиваются.

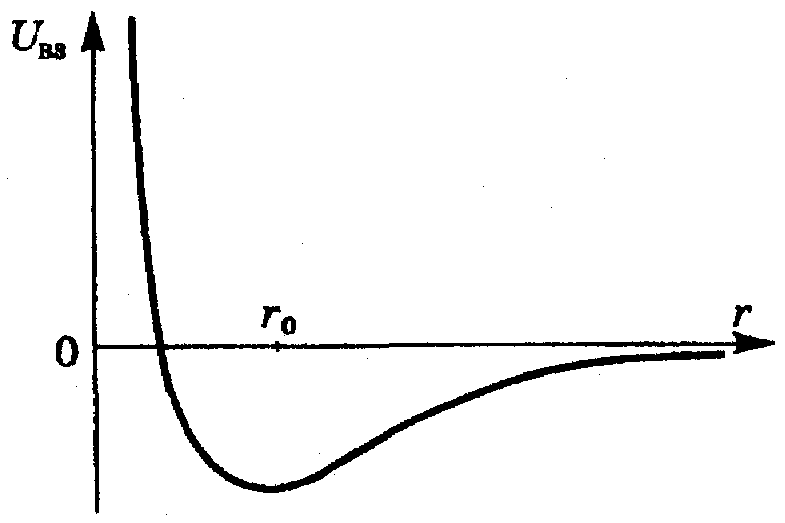
Рис. 5.1

Обе причины, не позволяющие адекватно описывать свойства реального газа при помощи уравнения Менделеева-Клапейрона, можно устранить, введя в него соответствующие поправки, что и сделал в 1873 году голландский физик Ван-дер-Ваальс¹. Уравнение, полученное Ван-дер-Ваальсом и носящее его имя, имеет следующий вид:

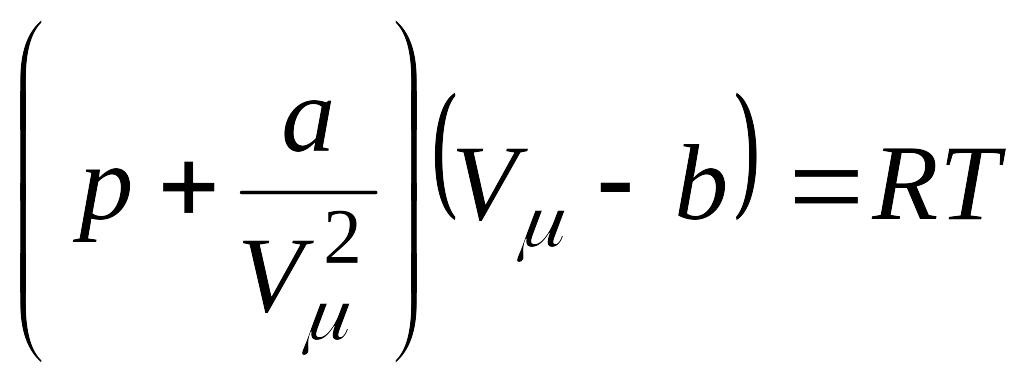. (5.1)

Постоянные а и b в уравнении (5.1) называются постоянными Ван-Дер-Ваальса. Значения постоянных а и b для некоторых газов приведены в таблице 5.1.

Таблица 5.1

Газ	а, Пам6/моль2	b, 10-6 м3/моль	d, нм
Н2	0,024	27	0,27
N2	0,137	39	0,37
O2	0,137	32	0,35
H2O	0,554	30	0,30

Поправка в первой скобке уравнения Ван-дер-Ваальса имеет размерность давления и называется внутренним давлением. Эта поправка описывает действие сил межмолекулярного взаимодействия. Смысл ее в том, что благодаря притяжению молекул друг к другу сила, с которой они действуют на стенку сосуда, уменьшается. Если бы силы межмолекулярного притяжения вдруг исчезли, давление на стенку сосуда возросло бы и стало бы равно .

Поправка b характеризует собственный объем молекул газ. Ее размерность метр кубический на моль (м³/моль). Можно показать, что

,

где d – эффективный диаметр молекулы² (см. таблицу 5.1).

Задача 5.1. Давление кислорода р равно 7 МПа, его плотность кг/м³. Найти температуру кислорода.

Решение

Поскольку давление кислорода p = 7 МПа  70 атм весьма велико, для нахождения его температуры воспользуемся уравнением Ван-дер-Ваальса (5.1). Учтем, что , где М = 0,032 кг/моль – молярная масса кислорода. Значения постоянных Ван-дер-Ваальса возьмем из таблицы 5.1: Пам⁶/моль², м³/моль. Имеем:

,

К.

Сравним полученный результат со значением температуры , рассчитанным по уравнению Менделеева-Клапейрона:

К.

Как видим, различие между Т и весьма существенно.