§ 4.4. Тепловые машины

Тепловыми машинами называются тепловые двигатели и холодильные машины (иначе – тепловые насосы). Тепловой двигатель - работающая по циклу машина, превращающая теплоту в механическую работу. Тепловые двигатели бывают самых разнообразных конструкций - двигатель внутреннего сгорания, паровой двигатель, турбина и т.д. Но независимо от конструкции любой тепловой двигатель содержит три основных структурных элемента: нагреватель, рабочее тело (или рабочее вещество) и холодильник (см. рис. 4.2). Нагреватель – часть двигателя, где сгорает топливо. Температуру нагревателя обозначим . За один цикл работы двигателя рабочее тело (газ) получает от нагревателя количество теплоты . В результате рабочее тело расширяется и совершает механическую работу А. После расширения рабочее тело должно вернуться в исходное состояние (сжаться). Опыт показывает, что в процессе сжатия от рабочего тела необходимо отвести «излишек» теплоты. Для этой цели служит холодильник. За один цикл работы рабочее тело отдает холодильнику теплоту (см. рис. 4.3). Температуру холодильника обозначим Т₂ ( ).

В основе работы теплового двигателя лежит замкнутый циклический процесс, следовательно, в конце каждого цикла состояние газа, являющегося рабочим телом, совпадает с его исходным состоянием, а значит изменение внутренней энергии газа за цикл равно нулю: . Согласно первому закону термодинамики работа, совершенная газом за цикл, будет равна полученной за цикл теплоте:

. (4.5)

Мерой эффективности теплового двигателя является его коэффициент полезного действия (КПД) , который определяется как

. (4.6)

КПД теплового двигателя всегда меньше единицы, поскольку соответствует случаю , т.е. процессу, единственным результатом которого было бы превращение теплоты, полученной от нагревателя, в работу, что запрещено вторым законом термодинамики в формулировке Кельвина.

Рис. 4.4

Задача 4.2. Рабочее вещество теплового двигателя совершает цикл, показанный на рисунке 4.4. Считая, что рабочее вещество является одноатомным идеальным газом, определите КПД  данного цикла.

Решение

Работу А, совершенную двигателем за один цикл, можно найти как площадь прямоугольника 1234 (см. § 3.2): . В § 3.3 было показано, что количество теплоты, полученное идеальным газом в изохорном процессе, равно , а в изобарном (в нашем случае число степеней свободы молекулы газа ). Используя данные формулы, найдем количество теплоты , полученное газом от нагревателя за весь цикл. Имеем:

, ,

, .

Таким образом, газ получает теплоту от нагревателя на участках цикла 12 и 34 ( ) и отдает на участках 34 и 41 ( . Следовательно,

. КПД цикла найдем по определению (4.6):

.

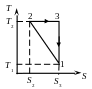
Рис. 4.5

Задача 4.3. Рабочее тело теплового двигателя совершает цикл, показанный на рисунке 4.5. В пределах цикла температура рабочего тела изменяется в n раз. Найдите КПД данного цикла.

Решение

Из определения энтропии (4.1) следует, что количество теплоты, полученное системой при переходе из состояния 1 в состояние 2 можно найти как . Таким образом, полученная газом теплота численно равна площади под графиком зависимости , причем при увеличении S и при уменьшении S. Следовательно, в нашем цикле газ получает теплоту от нагревателя на участке 23 ( ) и отдает теплоту холодильнику на участке 12 ( ). На участке 31 происходит адиабатное расширение газа ( ). Учитывая, что , находим:

,

,

.

Рис. 4.6 Рис. 4.7

В 1824 г. французский физик С.Карно¹ доказал, что максимальным КПД из всех возможных тепловых двигателей при заданных температурах нагревателя Т₁ и холодильника Т₂ обладает двигатель, работающий по циклу, состоящему из двух изотерм и двух адиабат (цикл Карно), как показано на рисунке 4.6.

Проанализируем цикл Карно. На участке 12 происходит изотермическое расширение газа. На этом этапе цикла газ находится в контакте с нагревателем, имеет температуру Т₁ и получает теплоту Q₁. Участок 23 - адиабатное расширение, во время которого газ совершает работу за счет уменьшения своей внутренней энергии. При этом температура газа уменьшается до температуры холодильника Т₂. Участок 34 - изотермическое сжатие при температуре Т₂. На данном этапе газ находится в контакте с холодильником и передает ему теплоту Q₂. Участок 41 - адиабатное сжатие, в результате которого температура газа повышается до Т₁, и газ возвращается в исходное состояние 1.

Найдем КПД цикла Карно, применив метод, использованный для решения задачи 4.3. Для этого изобразим цикл Карно на координатной плоскости (S,T) (см. рис. 4.7). Имеем:

. (4.7)

При выводе формулы (4.7) мы не делали никаких предположений о свойствах рабочего вещества и конструкции теплового двигателя. Отсюда следует теорема Карно: КПД теплового двигателя, работающего по циклу Карно, зависит только от температур нагревателя и холодильника и не зависит ни от устройства двигателя, ни от рода рабочего вещества.

Тепловой двигатель, работающий по циклу Карно, называют также идеальным тепловым двигателем.

Задача 4.4. Идеальный тепловой двигатель имеет КПД . Каким станет его КПД, если температуру нагревателя увеличить в 2 раза, а температуру холодильника уменьшить в 2 раза?

Решение

Воспользуемся формулой (4.7):

.

Обозначим новые температуры нагревателя и холодильника и , новый КПД – . Имеем:

, , .

Рис. 4.8

Любой циклический процесс идеального газа, протекающий достаточно медленно, можно считать обратимым. Следовательно, можно обратить цикл, по которому работает тепловой двигатель. При этом рарабочее тело за счет совершаемой над ним внешними силами работы А будет забирать теплоту Q₂ у холодильника и отдавать теплоту нагревателю (см. рис. 4.8). По такому принципу работают, например, бытовые холодильники. Таким образом, тепловой двигатель, работающий по обратному циклу, превращается в холодильную машину (или тепловой насос). Эффективность теплового насоса характеризуют при помощи так называемого холодильного коэффициента _х:

. (4.8)

Обратите внимание, что, в отличие от КПД теплового двигателя , холодильный коэффициент может быть и равен и больше единицы.

Задача 4.5. Тепловая машина, работающая по обратимому циклу Карно, является тепловым двигателем с КПД . Определите тепловой коэффициент _х той же тепловой машины, работающей по обратному циклу.

Решение

Воспользуемся формулами (4.6) и (4.8):

;

.

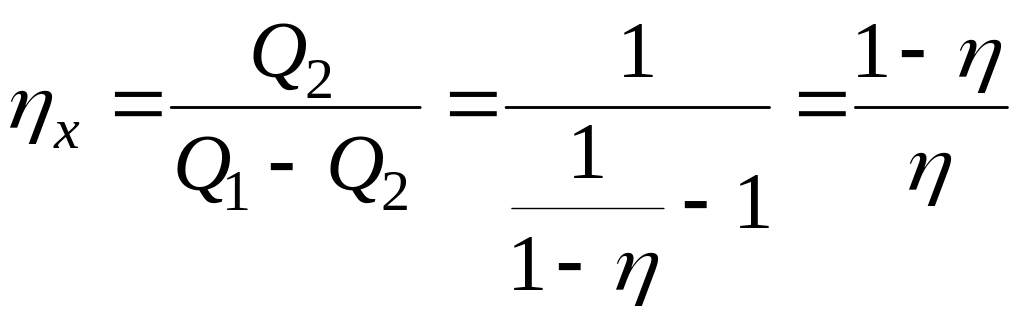Лекция 5. Реальный газ. Фазы и фазовые переходы