2. Определители

2.1. Основные понятия

Каждой квадратной матрице А n-ого прядка ставится в соответствии действительное число, обозначаемое символом det A или А, называемое определителем или детерминантом квадратной матрицы А и вычисляемое следующим образом:

1. n = 1

А = (a₁₁); det A = a₁₁

2. n = 2

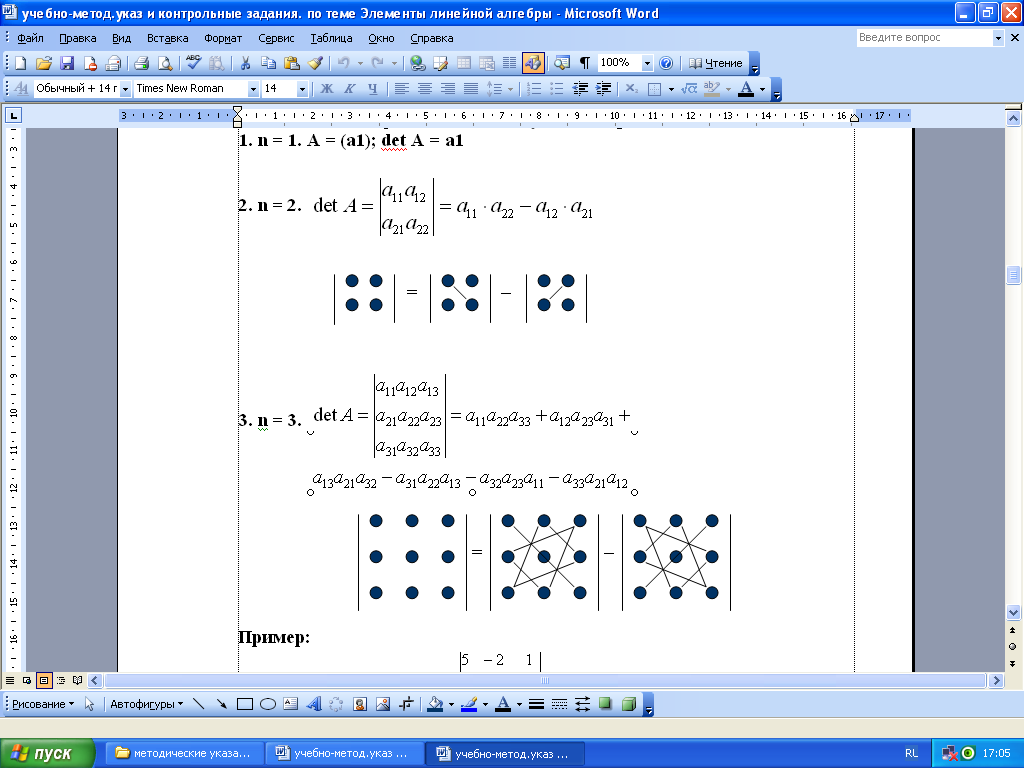
3. n = 3

Пример.

Найти определитель матрицы А, если

Решение:

Ответ: detA=9

5. Если n>3, то А вычисляется по специальному правилу, которое укажем далее.

2.2. Свойства определителей

1. Транспонирование определителя, т.е. замена строк столбцами и наоборот, не меняет его значения.

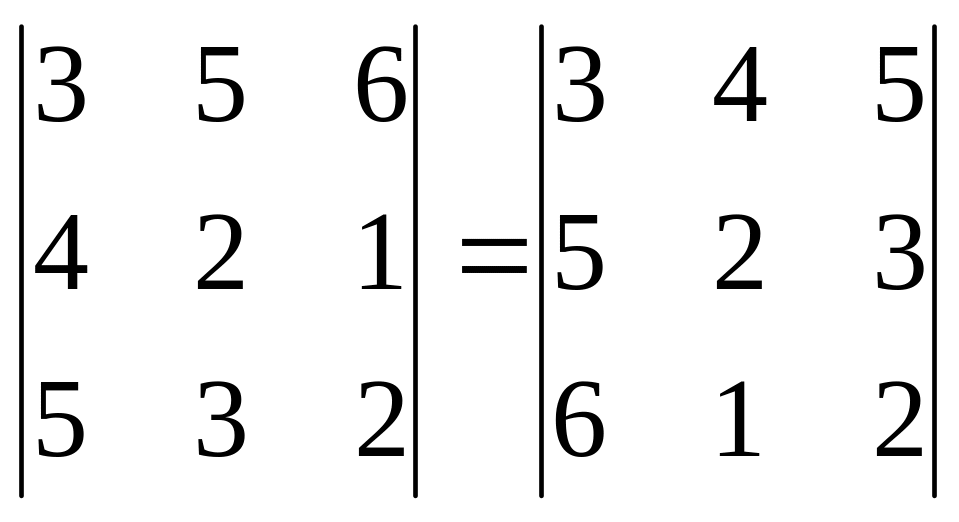
2. Перестановка любых двух строк (столбцов), меняет только знак определителя.

D = - D

3. Общий множитель всех элементов одной строки (столбца) может быть вынесен за знак определителя.

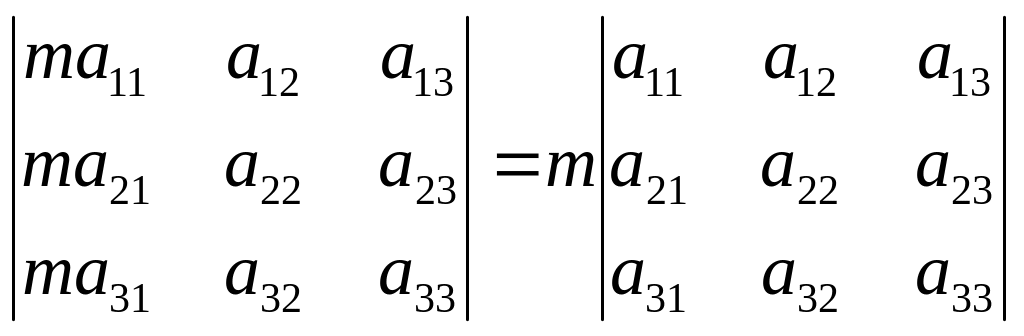
4. Если соответствующие элементы двух строк (столбцов) равны или пропорциональны, то определитель равен 0.

5. Если элементы какой-либо строки (столбца) определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

6. Определитель не изменится, если к элементам одной строки (столбца) прибавить соответствующие элементы параллельной строки (столбца), умноженные на любое число.

2.3. Минор элемента

Пусть дана квадратная матрица А=(а )

Минором некоторого элемента a_ij определителя n-го порядка матрицы А называется определитель (n-1)–го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент и обозначается М_ij.

Пример.

Найти минор элемента a₂₃ данного определителя.

Решение:

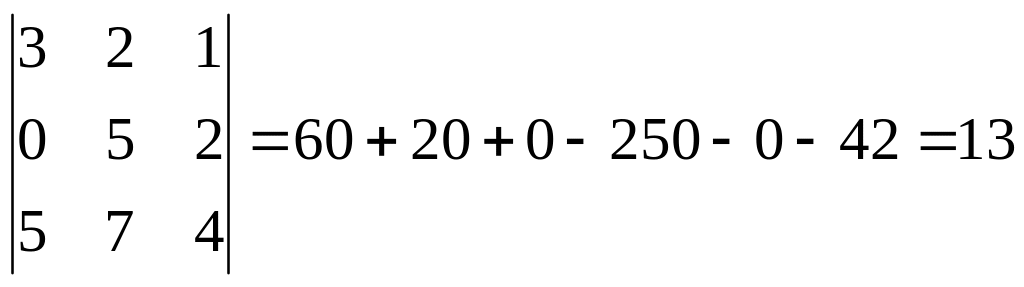
M₂₃ =

Ответ: М =13.

2.4. Алгебраическое дополнение

Алгебраическим дополнением A данного элемента определителя называется его минор М_ij, умноженный на , где i и j – номера строки и столбца на пересечении которых расположен этот элемент

Пример.

Найти алгебраическое дополнение элемента a₂₃ данного определителя.

Решение:

=-13

А₃₁=(-1) М₃₁=5

А₁₄=(-1) М₁₄=-11

Ответ: А =-13; А =5; А =-11

2.5. Формула Лапласа

Теорема. Определитель равен сумме произведений элементов всякой его строки (столбца) на их алгебраические дополнения.

Пример.

Найти определитель матрицы путем разложения по элементам 1 столбца, если

А=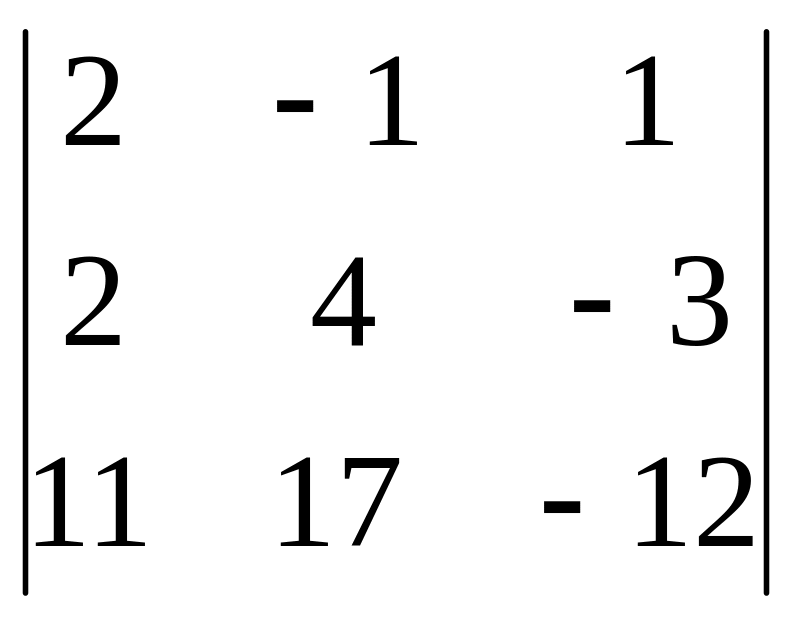

Решение:

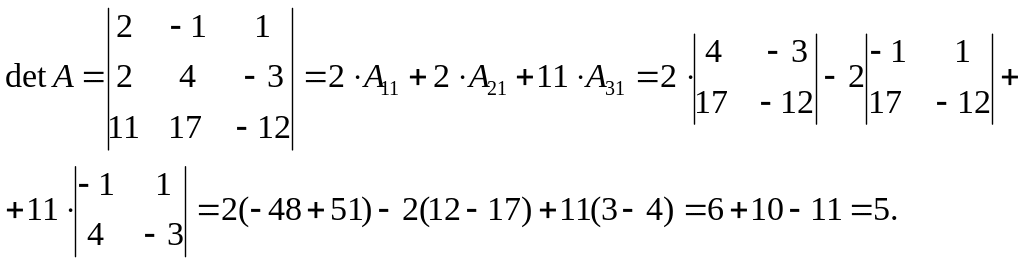
Ответ: detA=5.

2.6. Обратная матрица

Квадратная матрица А называется невырожденной, если det A не равен 0. В противном случае (det A равен 0) матрица А называется вырожденной.

Матрица А^-1 называется обратной квадратной матрице А, если выполняется условие:

,

где Е – единичная матрица того же порядка, что и матрица А. Матрица А^-1 имеет те же размеры, что и матрица А.

Теорема. Всякая невырожденная матрица имеет обратную.

Союзной к матрице А называется матрица вида:

,

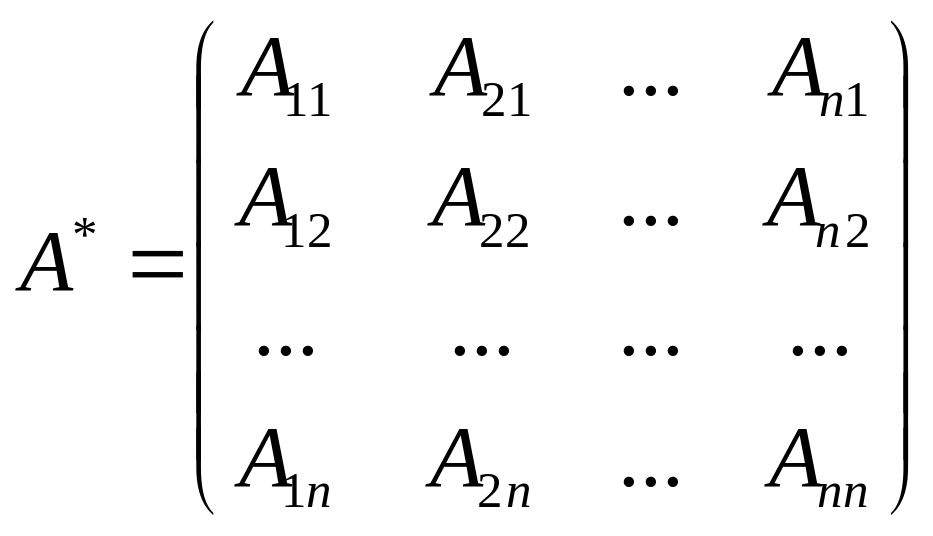где - алгебраическое дополнение элемента данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента определителя).

Алгоритм нахождения обратной матрицы

1. Найти определитель матрицы А.

det А ≠ 0

2. Составить матрицу А^* из алгебраических дополнений элементов А.

3. Транспонировать матрицу А^* для получения союзной матрицы А^*_т

4. Домножить матрицу А^*_т на 1/detA для получения обратной матрицы А^-1.

Свойства обратной матрицы

1. .

2. .

3. .

Пример:

Найти обратную матрицу для матрицы

А=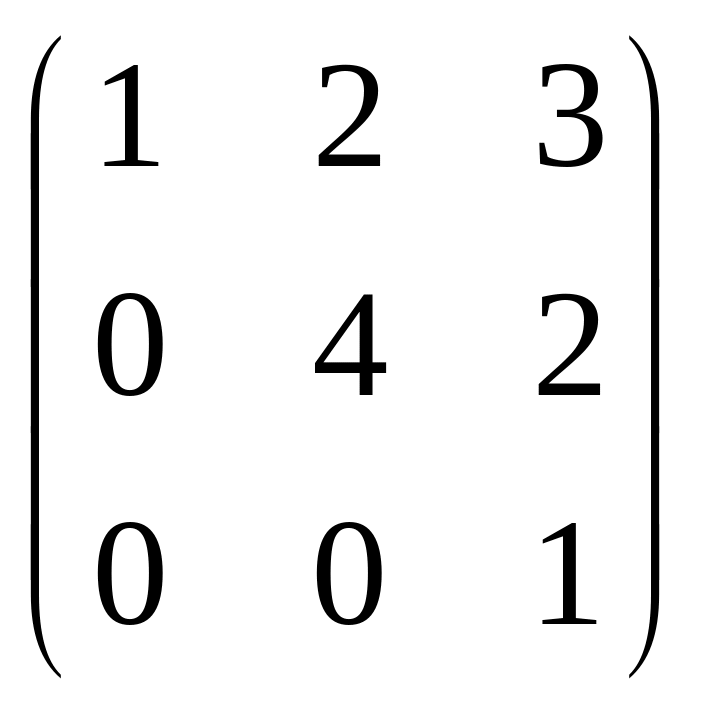

Решение:

Найдем определитель матрицы

detA=

Разложим этот определитель по элементам третьей строки, т.е.

detA=a ∙A +a ∙A +a ∙A =0+0+1∙ =4

A = =4, А =- =0, А =- =0, А = =0

A = =-2, А = =1, А =- =0, А = =-8,

А =- =-2, А = =4

Следовательно:

=

Далее: =

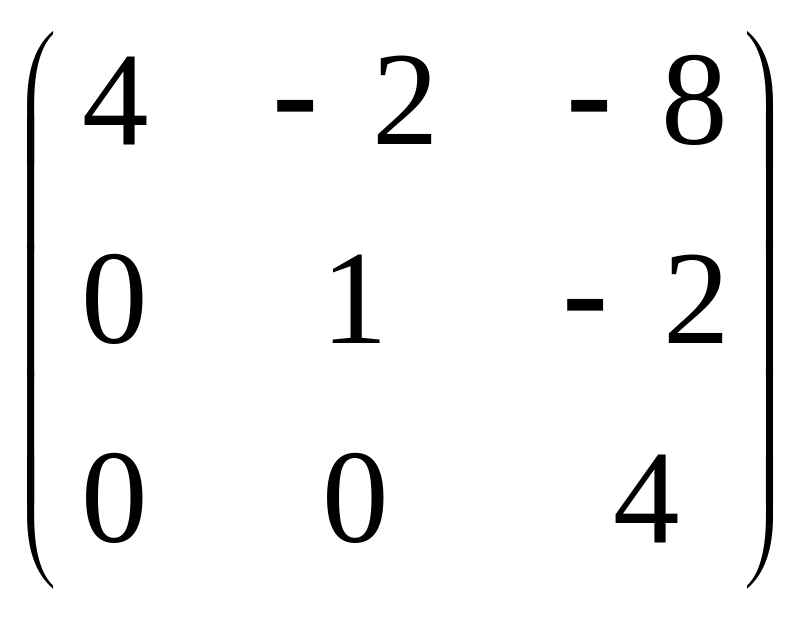
Находим:

А =1/4∙ =

Делаем проверку

А∙А = ∙ =

Ответ: А =