§6. Выдающиеся м-ки 18 века.

Якоб Бернулли (1654-1705), профессор м-ки Базельского ун-та (с 1687г.) (швейцарский математик), и его младший брат Иоганн Бернулли (1667-1748) вели оживленную переписку с Лейбницом и сумели еще больше расширить рамки применения его методов. Еще до получения каких-либо разъяснений от Лейбница Якоб Бернулли, пользуясь введенными новыми методами, разрешил задачу о так называемой брахистохроне. Эта задача заключалась в нахождении кривой быстрейшего спуска, то есть такой кривой, по которой материальная точка в поле тяжести, двигаясь под действием только сил этого поля и с начальной скоростью, равной нулю, перейдет из одного наперед заданного положения в другое тоже заданное, за кратчайший срок. Якоб Бернулли показал, что этой кривой является циклоида. В этой работе Якоб Бернулли, употребляя введенный Лейбницом символ , впервые наименовал его интегралом. Бернулли, широко применяя эти исчисления, разрешил ряд геометрических задач. Так, им была получена формула для определения радиуса кривизны плоской кривой. Им изучены также многие кривые. Он открыл и изучил лемнискату-кривую, произведение расстояний которой от двух постоянных точек (фокусов) равно постоянной величине .

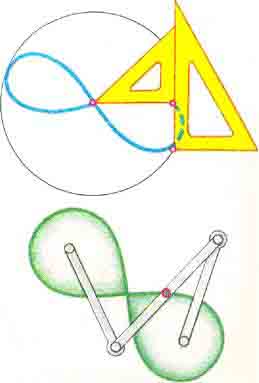
Эта линия изображена на рисунках (см. ниже), по форме напоминает восьмерку. Якоб Бернулли дал этой кривой поэтическое название «лемниската». В античном Риме так называли бантик, с помощью которого прикрепляли венок к голове победителя на спортивных играх. Рассмотриm два способа построения лемнискаты. Один из них с помощью двух угольников и нарисованной на листе бумаги окружности. Вершина острого угла одного из угольников находится в центре окружности, вершина прямого угла другого - на окружности. Другой способ построения лемнискаты Бернулли - с помощью шарнирного устройства, две точки которого закреплены на плоскости.

Уравнение лемнискаты в прямоугольных координатах: , уравнение в полярных координатах:

Якоб Бернулли впервые обнаружил расходимость гармонического ряда.

После смерти Я. Бернулли в 1705 г. кафедра м-ки перешла к его брату Иоганну Бернулли, занимавшему до того времени кафедру м-ки Гронингенского ун-та в Голландии. Работы И. Бернулли по м-му анализу оказали положительное влияние на развитие вопроса о дифференциальных ур-х, так называемого ур-я Бернулли, а также ур-я с постоянными коэффициентами. Решая задачи геометрического характера на спрямление кривых и вычисление квадратур, И.Бернулли совершенствовал и развивал методы интегрирования рациональных дробей.

Братья Бернулли, решая задачи, связанные с понятиями максимума и минимума, пришли к вопросам, из которых впоследствии выросла особая отрасль м-х наук, называемая вариационным исчислением.

Маркиз Гильом Франсуа Лопиталь(1661-1704) сумел хорошо использовать те знания, которые он получил от И.Бернулли, и в 1696 г. издал книгу «Анализ бесконечно малых», к-рая считается первым систематическим изложением дифференциального исчисления.

Жозеф Луи Лагранж (1736-1813), француз, ввел понятие о производных разных порядков как о коэффициентах разложения функций в степенной ряд. Ему удалось подойти к понятиям анализа исходя из понятий алгебры конических величин. Им дана очень удобная для практики формула выражения остаточного члена ряда Тейлора, разработана теория условных максимумов и минимумов, дан метод вариации произвольных констант при решении линейных дифференциальных ур-ний. В элементарной алгебре разработал теорию цепных дробей. Продвинул теорию чисел, в которой он исследовал квадратичные вычеты, среди ряда других теорем доказал то, что каждое целое число есть сумма четырех или меньшего числа квадратов.

Жан Лерон Д Аламбер (1717-1783), он хотел обосновать анализ, построив его впервые на теории пределов. Работы в области теории рядов дифференциальных ур-ний. Им получен признак сходимости ряда с положительными числами. В значительной степени способствовал развитию теории дифференциальных ур-ний с постоянными коэффициентами, СЛУ первого и второго порядка. Им дано решение дифференциального ур-ния второго порядка частных производных − ур-ние м-кой физики, дающее выражение поперечных колебаний струны − волновое ур-ние. В его работах впервые встречается практическое применение функций комплексного переменного.

Д Аламбером и Эйлером открыты условия дифференцируемости функций комплексного переменного.

Огюстен Луи Коши (1789-1857), выдающийся французский математик, родился в Париже. Основные м-кие работы Коши: «Курс анализа», «Резюме лекций по исчислению бесконечно малых». Кроме того, имеют большое значение его многочисленные работы по дифференциальным уравнениям и теории комплексного переменного, а также по алгебре, где, например, разработана теория детерминантов. Коши углубил теорию дифференциальных уравнений, доказав существование в области, не содержащих особых точек, решений системы дифференциальных уравнений, удовлетворяющих определенным условиям.

Алексис Клод Клеро (1713-1765), уже в возрасте 12 лет представил в Парижскую академию наук доклад об особых кривых, в котором было проведено исследование одного типа алгебраических кривых четвертого порядка. В 1729 г. oн написал большую работу «Изыскание о кривых двоякой кривизны». Эта работа произвела большое впечатление на членов Академии, и Клеро было присвоено звание действительного члена Академии наук, когда ему исполнилось 17 лет. Указанная работа имела большое значение в развитии геометрии, т.к. она с работами Эйлера положила начало серьезному изучению криволинейных стереометрических образов. Клеро впервые ввел понятие полного дифференциала функции нескольких независимых переменных.

Гаспар Монж (1746-1818) происходил из семьи крестьянина, который занимался мелкой торговлей. Отец Монжа дал своим сыновьям такое хорошее образование, что все стали впоследствии профессорами м-ки. Профессор Мезьерской военно-инженерной школы (с 1768), один из основателей и профессор Политехнической школы в Париже (с 1794).

М-ка обязана Монже зарождением новой отрасли м-ких знаний – начертательной геометрии, творцом которой он справедливо считался («Начертательная геометрия»).

Исходя из идеи проектирования предметов на две взаимно перпендикулярные плоскости, создал общий метод изображения пространственных фигур на плоскости. Работы в этой области были выполнены Монже в первые годы его деятельности в Мезьерской школе (до середины 70-х гг.), однако написанный им труд «Начертательная геометрия» был издан только в 1799. В работах «Мемуар о развёртках, радиусах кривизн и различных родах перегиба кривых двоякой кривизны» (1771, изд. 1785) и «О свойствах многих родов кривых поверхностей...» (1775, изд. 1780) Монже дал обстоятельное изложение дифференциальной геометрии пространственных кривых и поверхностей: изучил эволюты пространственных кривых, кривизны поверхностей, исследовал огибающие, развёртывающиеся поверхности. (Развёртывающиеся поверхности это такие поверхности, которые могут быть совмещены с плоскостью без разрывов и складок. К этому типу относятся все многогранные поверхности, цилиндрические, конические и торсы. Все остальные кривые поверхности не развертываются на плоскость и поэтому при необходимости изготовления этих поверхностей из листового материала их приближенно заменяют развертывающимися поверхностями. У развертывающихся поверхностей смежные образующие параллельны или пересекаются.) В 1881 рассмотрел общие свойства нормальных конгруэнций и ввёл в науку линии кривизны поверхностей. В труде Монже «Приложение анализа к геометрии» (1795), помимо важных открытий по дифференциальной геометрии, дано геометрическое истолкование уравнений с частными производными и, с другой стороны, изложение геометрических фактов на языке уравнений с частными производными.

(В период Великой французской революции Монже состоял в комиссии по установлению системы мер и весов, в 1792-93 был морским министром. В 1793 заведовал пороховыми и пушечными заводами республики. Активно участвовал в создании Высшей нормальной школы (1794), Политехнической школы (1794). В период Директории Монже сблизился с генералом Бонапартом, участвовал в его египетской экспедиции 1798-1801. Вернулся во Францию вместе с Бонапартом; возобновил преподавание в Политехнической школе. Во времена Первой империи Монже стал сенатором, получил титул графа. В период Реставрации М. был лишён всех прав и изгнан из Политехнической школы и Академии наук).

Карл Фридрих Гаусс (1777-1855) родился в семье бедного водопроводчика в г. Брауншвейге. Высшее образование ему удалось получить в Геттингенском университете благодаря покровительству герцога, имевшего случай убедиться в необыкновенных способностях мальчика (мальчик бывает во дворце и развлекает придворных искусством счета). 

Первое обширное сочинение Гаусса «Арифметические исследования» (опубликовано в 1801) на многие годы определило последующее развитие двух важных разделов математики — теории чисел и высшей алгебры. Из множества важных и тонких результатов, приведенных в «Арифметических исследованиях», следует отметить подробную теорию квадратичных форм и первое доказательство квадратичного закона взаимности. В конце сочинения Гаусс приводит полную теорию уравнений деления круга и, указывая их связь с задачей построения правильных многоугольников, решает стоявшую с античных времен проблему о возможности построения циркулем и линейкой правильного многоугольника с заданным числом сторон. Гаусс указал все числа, при которых построение правильного многоугольника с помощью циркуля и линейки возможно. Это пять так называемых гауссовых простых чисел: 3, 5, 17, 257 и 65337, а также умноженные на любую степень двойки произведения различных (не повторяющихся) гауссовых чисел. Например, построить с помощью циркуля и линейки правильный (3х5х17)-угольник можно, а правильный 7-угольник нельзя, так как семерка не гауссово простое число.

Доказанный Гауссом результат — пример так называемой чистой теоремы существования; утверждается, что построить с помощью циркуля и линейки правильный многоугольник с «допустимым» числом сторон можно, но ничего не говорится о том, как это сделать. Карл Гаусс предложил также явный способ построения с помощью циркуля и линейки правильного 17-угольника. Это событие Гаусс посчитал столь значительным, что отметил его в «Дневнике» (запись от 30 марта 1796) и завещал высечь правильный 17-угольник на своем надгробии (воля Гаусса была исполнена).

С именем Гаусса также связана основная теорема алгебры, согласно которой число корней многочлена (действительных и комплексных) равно степени многочлена (при подсчете числа корней кратный корень учитывается столько раз, какова его степень). Первое доказательство основной теоремы алгебры Гаусс дал в 1799, а позднее предложил еще несколько доказательств.

В 1812 Карл Гаусс познакомил математический мир со своей гипергеометрической функцией, частным случаем которой являются многие из так называемых специальных функций математической физики. В той же работе он рассматривает и вопросы сходимости бесконечных рядов, важные для астрономических вычислений.

В 1818 Карл Гаусс одним из первых начинает размышлять над созданием неевклидовой геометрии, но от публикации полученных результатов воздерживается, опасаясь, по собственному признанию, «криков беотийцев» (т.е. возражений и насмешек невежд).

Десятилетие 1820-30 застает Гаусса за проведением геодезической съемки Ганноверского королевства и составлением его подробной карты. Гаусс не только проделывает огромную организационную работу и руководит измерением длины дуги меридиана от Геттингена до Альтоны, но и создает основы «высшей геодезии», занимающейся описанием действительной формы земной поверхности. Обобщающий труд «Исследования о предметах высшей геодезии» Гаусс создает в 1842-47. В основе этого фундаментального труда лежат также принадлежащие Гауссу идеи так называемой внутренней геометрии поверхности, изложенной им в сочинении «Общие исследования о кривых поверхностях» (1827). Локальные (т. е. характеризующие малую окрестность точки) свойства поверхности, по мысли Гаусса, естественнее связывать не с «посторонними», введенными извне, а с внутренними криволинейными координатами и выражать через дифференциальную форму от внутренних координат. Если поверхность изгибать не растягивая, то ее внутренние свойства остаются неизменными. Впоследствии по образу и подобию внутренней геометрии поверхностей Гаусса была создана многомерная риманова геометрия.

В исследованиях о биквадратных вычетах (в работах 1825 г. 1831 г.) Гауссом впервые было представлено мнимое число в виде a+bi. После Гаусса в употребление и геометрическое истолкование мнимых и комплексных чисел, но оно создавалось постепенно.

Каспер Вессель (1745-1818), датский землемер и математик. В работе «Об аналитическом представлении направлений» (1799) посвященной теории векторов на плоскости и в пространстве, дал впервые геометрическую интерпретацию комплексных чисел на плоскости, но его работа, написанная на датском языке, не получила распространения, а потому вопрос о геометрическом представлении комплексных чисел в дальнейшем разрабатывался другими математиками совершенно независимо от Веселя.