35.1Задания для самостоятельного выполнения
Сколько существует вариантов размещения n товаров на полке?
Вариант
n
Результат
1
7
5 040
2
9
362 880
3
11
39 916 800
4
5
120
5
8
40 320
6
10
3 628 800
7
12
479 001 600
8
6
720
9
14
87 178 291 200
10
13
6 227 020 800
Сколько различных списков подгрупп из n человек можно составить в группе из m человек?
Вариант
n
m
Результат
1
5
16
4 368
2
5
17
6 188
3
6
18
18 564
4
7
20
77 520
5
8
24
735 471
6
8
25
1 081 575
7
9
26
3 124 550
8
10
27
8 436 285
9
12
30
86 493 225
10
15
30
155 117 520
В супермаркете есть n точек для размещения товаров. На каждой точке размещаются товары одного вида. Сколько способов существует для размещения товаров m видов, если один вид товара размещается не более чем на одной точке?
Вариант
n
m
Результат
1
3
67
287 430
2
5
27
9 687 600
3
4
25
303 600
4
2
48
2 256
5
2
135
18 090
6
4
55
8 185 320
7
3
90
704 880
8
5
60
655 381 440
9
4
120
197 149 680
10
2
311
96 410
Вычислить математическое ожидание, дисперсию, стандартное отклонение, а также квартили и персентили для случайных величин
Ряды дискретных случайных величин
Квартиль
Персентиль для p-квантили
№
p-квантиль
10,00
14,00
5,00
6,00
10,00
12,00
13,00
7,00
6,00
8,00
3
11,50
0,10
5,90
0,20
0,50
2,00
3,00
5,10
8,00
2,00
4,00
0,30
3,00
2
2,50
0,20
0,46
31,00
14,00
21,00
32,00
11,00
21,00
17,00
64,00
12,00
9,00
3
28,50
0,30
13,40
9,00
3,00
5,00
2,00
11,00
8,00
6,00
5,00
4,00
3,00
1
3,25
0,40
4,60
0,20
1,50
2,00
1,00
0,80
0,25
6,00
5,00
4,00
3,00
4
6,00
0,50
1,75
18,24
5,65
6,10
5,50
8,43
2,80
5,80
16,10
18,17
14,60
2
7,27
0,60
10,90
17,16
3,40
5,80
4,40
7,18
0,45
4,80
15,80
18,14
13,60
3
15,25
0,25
4,50
16,08
1,15
5,50
3,30
5,93
1,90
3,80
15,50
18,11
12,60
1
3,43
0,35
4,06
15,00
1,10
5,20
2,20
4,68
4,25
2,80
15,20
18,08
11,60
4
18,08
0,45
4,71
13,92
3,35
4,90
1,10
3,43
6,60
1,80
14,90
18,05
10,60
3
13,09
0,55
6,52
При бросании монеты может выпасть «орел» или «решка». Вероятность того, что при очередном бросании выпадет «орел», равна 0,5. Вычислите вероятность того, что «орел» выпадет точно n раз из m.
Вариант
Успех, n
Число испытаний, m
Результат
1
6
10
0,205078
2
10
15
0,091644
3
12
20
0,120134
4
13
25
0,154981
5
13
30
0,111535
6
17
35
0,132061
7
23
40
0,080702
8
21
45
0,107254
9
23
50
0,095962
10
32
55
0,051804
При бросании игральной кости может выпасть одна из граней (от 1 до 6). Вероятность того, что при очередном бросании выпадет «2», равна 1/6. Вычислите вероятность того, что «2» выпадет точно 10 раз из 42 бросков. (0,07)
Магазин продает женскую обувь. Распределение спроса по размерам является нормальным с математическим ожиданием М=37 и сигма=1. Вычислите процент спроса на 34 размер. (0,44%)
Сколько трехзначных чисел можно составить из цифр 7, 9, 6, 5, 4? (60)
Ежедневные расходы на обслуживание и рекламу автомобилей в автосалоне составляют в среднем 130 тыс. ден. ед., а число продаж (Х) автомашин в течение дня подчиняется закону распределения, заданному таблицей. Требуется вычислить математическое ожидание ежедневной прибыли при цене автомашины в 150 тыс ден. ед. (271250)
Х (число продаж) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Р (вероятность) |
0,25 |
0,2 |
0,1 |
0,1 |
0,1 |
0,1 |
0,05 |
0,05 |
0,025 |
0,025 |
Вычислить дисперсию ежедневной продажи автомашин по данным таблицы (6,23)
Х (число продаж) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Р (вероятность) |
0,15 |
0,05 |
0,1 |
0,15 |
0,07 |
0,17 |
0,14 |
0,12 |
0,025 |
0,025 |
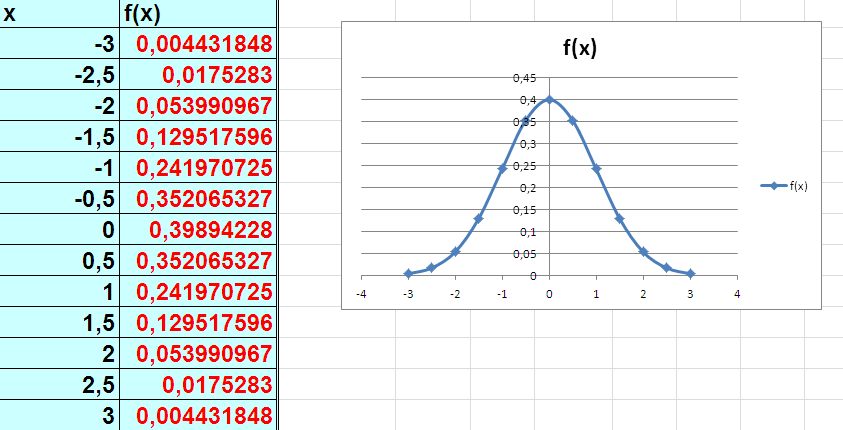
Постройте диаграмму стандартного нормального интегрального распределения (стандартное нормальное распределение имеет M=0 и сигма=1) в диапазоне [-3;3].
Результат
