
Лекция 12
.pdfТема 4. Методы второго порядка
4.1. Метод Ньютона
Исторически метод Ньютона является первым из методов, основанных на квадратичной аппроксимации минимизируемой функции F . Такая аппроксимация, оставаясь достаточно простой, в то же время намного точнее, чем линейная (метод наискорейшего спуска), следовательно, можно разработать более эффективные методы. В качестве квадратичной модели целевой функции F можно взять сумму первых 3-х членов разложения F в
ряд Тейлора в окрестности текущей точки |
xk (на примере |
|
одномерной |
|||||||
функции): |
|
|
|
|
|
|
|
|
|
|
f ( x) |
f ( xk ) |
f |
|
( xk )( x |
xk ) |
1 |
|
|
2 |
(4.1.17) |
|
|
|
||||||||
|
2 |
f ( xk )( x xk ) |
|
|||||||
|
|
|
|
|
|
|
|
|
||
min f ( x) ищем из необходимого условия экстремума I порядка: |
||||||||||
|
|
|
|
|
|
|
|
|
|
(4.1.18) |
|
|
f ( xk ) f |
( xk )( x xk ) 0. |
|
||||||
Решая полученную систему линейных уравнений и принимая найденную точку минимума за xk 1 , получим (для одномерного случая):
xk 1 xk hk |
, где hk |
f |
|
( xk ) |
|
(4.1.19). |
||
|
||||||||
f |
|
( xk ) |
||||||
|
|
|
||||||
|
|
|
|
|
||||
Алгоритм минимизации, в котором направление pk определяется из (4.1.19), называют методом Ньютона, а решение этой системы – ньютоновским направлением. Итерационный процесс (4.1.19) строит последовательность точек xk , которая при определенных предположениях
сходится к некоторой стационарной точке x* функции f ( x). Если матрица Гессе f ( x* ) положительно определена, эта точка будет точкой строгого локального минимума f ( x).
1
В точке xk функция |
f ( x) |
~ |
аппроксимируется параболой f ( x), а в |
||
качестве приближения |
xk 1 |
принимается точка, соответствующая |
минимальной ординате этой параболы.
Метод Ньютона более эффективен (меньшее число итераций), чем градиентные методы, т.к. квадратичная функция локально точнее аппроксимирует минимизируемую функцию, чем линейная (основа
градиентных методов). В градиентных методах приходится выбирать шаг k
вдоль направления антиградиента в точке xk , т.к. линейная функция не имеет точек экстремума. В методе Ньютона аппроксимирующая квадратичная функция (4.1.17) имеет конечную точку минимума, поэтому
|
|
|
f |
|
( xk ) |
|
|
|
шаг вдоль направления на эту точку |
|
|
|
|
не выбирается, а |
|||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
f |
( xk ) |
|
|||
|
|
|
|
|
||||
полагается равным 1.
Рассмотрим метод Ньютона в пространстве E2 и продемонстрируем важность положительной определенности матрицы Гессе целевой функции
xk 1 |
xk |
|
1 |
|
|
(4.1.20) |
||
( f ( xk )) |
|
f ( xk ), |
||||||
|
( xk )) |
1 |
– обратная к матрице Гессе. |
|
||||
где матрица ( f |
|
|
||||||
Аппроксимирующая функция для функции 2-х переменных выглядит следующим образом:
|
|
f ( xk ) ( f |
|
( xk ), x xk ) |
1 |
|
|
|
|
|
|
||||
f ( x) |
|
|
|
|
|
|
|||||||||
|
2 |
( f ( xk )( x xk ), x xk ) . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
( x1 , x2 ) ( x, y) X , |
|
|
квадратичная |
|
форма |
|||||||||
f ( X |
k |
) b b x |
k |
b y |
b x2 |
b |
|
y2 |
b x |
y |
b y x |
k |
(4.1.21) |
||
|
0 1 |
|
|
2 k |
11 k |
22 k |
12 |
k k |
21 k |
|
|||||
преобразовывается к каноническому виду (с помощью переноса системы координат и поворота осей):
|
|
* |
~ ~2 |
~ ~2 |
|
f ( Xk ) f ( x |
) b11 xk |
b22 yk |
, |
||
|
|
|
2 |
|
|

где |
x* – стационарная точка функции |
f . Коэффициенты квадратичной |
|||||||||||||||||||||
формы (4.1.21) связаны с элементами матрицы Гессе |
f ( x) |
следующим |
|||||||||||||||||||||
образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
b |
1 2 f |
, b |
|
|
1 2 f |
|
1 2 f |
b , |
b |
1 2 |
f |
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 x |
|
|
|
|
x y |
2 y x |
2 y |
|
|
||||||||||||||
11 |
|
2 |
12 |
|
2 |
|
|
21 |
22 |
2 |
|
|
|||||||||||
|
|
|
|
|
~ |
|
~ |
|
|
|
|
|
|
|
|
|
|
1 |
|
f |
|
( xk ). Если |
|
Коэффициенты b11 |
и b22 – собственные значения матрицы |
|
|
||||||||||||||||||||
2 |
|
||||||||||||||||||||||
|
|
||||||||||||||||||||||
~ |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
b11 |
0,b22 |
то |
|
|
f ( x) |
имеет вид кругового или эллиптического |
|||||||||||||||||
параболоида (рис. 4.1.15).
|
|
|
Рис.4.1.15 |
~ |
~ |
0, то |
|
Если b11 |
b22 |
f ( x) описывает гиперболический параболоид, |
поверхность с седловой точкой (рис. 4.1.15). Эта точка будет взята в качестве
следующего приближения xk 1 в методе Ньютона, |
хотя может оказаться, |
|||||||
что f ( x |
k 1 |
) f ( x |
k |
). Это может привести к тому, |
что f ( x |
) f ( x |
k |
) , |
|
|
|
k 1 |
|
|
|||
и вместо приближения к искомой точке минимума x* |
будет удаление от нее. |
|||||||
Т.о. сходимость метода Ньютона обеспечена лишь в случае положительной определенности матрицы Гессе целевой функции на каждой итерации.
3

Рис. 4.1.16
~ ~
Если b11 и b22 одного знака, но сильно отличаются по величине, график квадратичной функции (4.1.21) имеет «овраг». В этом случае градиентные методы работают плохо, а метод Ньютона находит минимум
квадратичной |
функции |
за |
один |
шаг, |
независимо |
от |
x0 и |
степени |
||||||||||
«овражности». |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В примере 16 |
для функции |
f ( X ) x2 |
16 y2 |
«овраг» вытянут |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
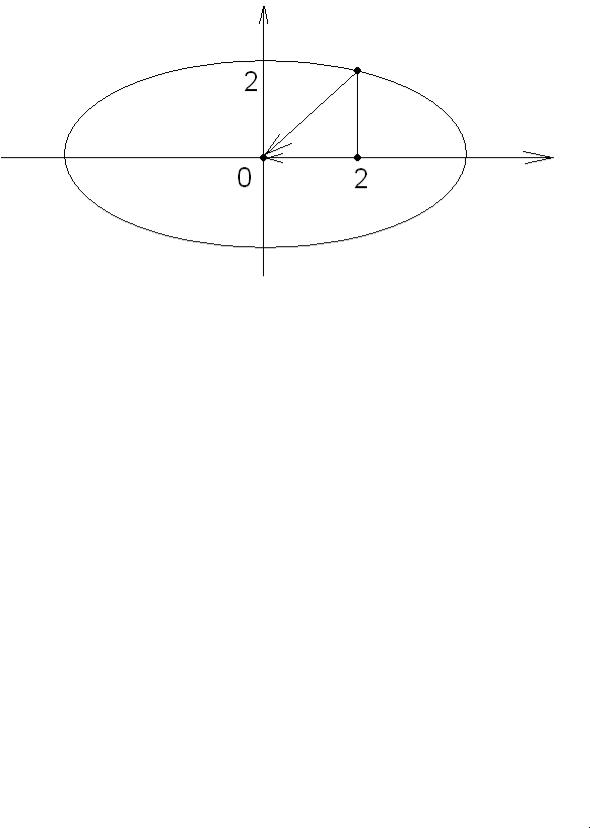
вдоль оси ОХ. Убедимся, что направление спуска – ( f ( x0 )) |
|
f ( x0 ), |
||||||||||||||||
вычисленное в различных точках |
x0 , всегда совпадает с направлением в |
|||||||||||||||||
точке минимума x* |
(0,0)T (рис. 4.1.17). |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
Пусть x0 |
|
|
|
|
T |
|
|
|
|
T |
( x0 ) |
|
|
, |
||||
|
(2,2) |
, тогда f ( x0 ) |
(4.64) , f |
|
0 |
32 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( f ( x0 )) 1 |
1 |
|
|
32 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
64 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( f ( x0 )) 1 |
|
|
|
|
|
|
1/ 2 |
0 |
|
4 |
2 |
|
|
|
|
|
|
|
f ( x0 ) |
|
|
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
0 1/ 32 |
|
64 |
2 |
|
|
|
|
|
|
|
|
4
|
(2,0)T , тогда ( f ( x0 )) 1 |
|
2 |
|
Пусть x0 |
f ( x0 ) |
0 |
. |
|
|
|
|
|
Рис.4.1.17
В общем случае, когда минимизируемая функция не квадратична,
вектор ( f ( xk )) 1 f ( xk ) не указывает в точку ее минимума, однако имеет большую составляющую вдоль оси «оврага» и значительно ближе к направлению на минимум, чем антиградиент. Этим и обусловлена более высокая сходимость метода Ньютона по сравнению с градиентным при минимизации «овражных» функций, которые встречаются довольно часто.
Метод |
|
Достоинства |
|
|
Недостатки |
|
|
|
|
|
|
Градиен- |
1. |
Глобальная сходимость |
|
1. |
Медленная сходимость |
тный |
2. |
Слабые требования |
к |
2. |
Необходимость выбора шага |
|
|||||
|
f ( x) |
|
k |
||
|
3. |
Простота вычислений |
|
|
|
|
|
|
|
|
|
Метод |
1. |
Быстрая сходимость |
|
1. |
Локальная сходимость |
Ньютона |
|
|
|
2. |
Жесткие требования к f ( x) |
|
|
|
|
||
|
|
|
|
3. |
Большой объем вычислений |
|
|
|
|
|
|
5
Основные недостатки: 1) предполагает вычисление вторых производных, что может быть связано с существенными трудностями; 2) может расходиться, если целевая функция не является сильно выпуклой и начальное приближение находится достаточно далеко от минимума.
Теоремы о сходимости метода Ньютона.
|
Определение: Числовая функция f ( x) на Rn |
называется выпуклой, |
|
если |
для |
x, y Rn , |
0 1, |
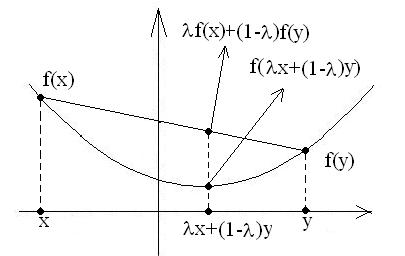
f ( x (1 ) y) f ( x) (1 ) f ( y) . |
|
||
Геометрический смысл выпуклой функции приведен на рис. 4.1.18.
|
Рис.4.1.18 |
|
|
График функции на x, y |
лежит |
ниже |
хорды, соединяющей точки |
( x, f ( x)), ( y, f ( y)). |
|
|
|
Определение: Функция |
f ( x) |
на Rn |
называется строго выпуклой, |
если для x y,0 1 |
|
|
|
f( x (1 ) y) f ( x) (1 ) f ( y)
исильно выпуклой с константой r 0, если при 0 1
f ( x (1 ) y) f ( x) (1 ) f ( y) |
r (1 ) |
|
|
x y |
|
|
|
2 . |
|
|
|
|
|
||||||
|
|||||||||
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
6 |
|
|
|
|
|
|
|
|
|
Для дифференцируемой функции f ( x) на |
Rn сильная выпуклость |
|||||||||||||||||||||||||||||||||||||||||
эквивалентна неравенству |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x, y R |
|
|
f ( x y) |
f ( x) ( f |
x , y) 2 |
|
|
y |
|
. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Наиболее просто критерий сильной выпуклости формулируется для |
||||||||||||||||||||||||||||||||||||||||||
дважды дифференцируемых |
|
|
функций |
|
|
f ( x): |
|
|
сильная |
|
выпуклость |
|||||||||||||||||||||||||||||||
эквивалента условию |
|
f |
|
( x) lE , где E – единичная матрица. |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||
Теорема 1: Пусть функция |
|
|
|
f ( x) |
|
|
|
|
|
– дважды |
дифференцируема, |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( x) удовлетворяет условию Липшица с константой R : |
|
|
|
|||||||||||||||||||||||||||||||||||||||
x, y En |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
x y |
|
, |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
f ( x) |
f ( y) |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
f ( x) сильно выпукла с константой r |
и |
|
начальное |
приближение x0 |
||||||||||||||||||||||||||||||||||||||
удовлетворяет условию |
q |
|
|
R |
|
|
|
|
|
f ( x0 ) |
|
|
|
|
1, |
тогда |
метод Ньютона |
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
2r 2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
сходится к точке глобального минимума x* |
с квадратичной скоростью |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
n |
x* |
|
|
|
|
2r |
q2n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Условия теоремы 1 можно несколько ослабить лишь в одном направлении –
можно глобальные требования к функции |
f ( x) заменить на локальные. |
|||||||||||||||||||
|
|
Теорема 2: Пусть |
f ( x) дважды дифференцируема в окрестности U |
|||||||||||||||||
точки |
невырожденного |
минимума x |
* |
и |
|
|
|
|
|
|||||||||||
|
f ( x) удовлетворяет условию |
|||||||||||||||||||
Липшица на U . Тогда найдется 0 |
такое, что при |
|
|
|
метод |
|||||||||||||||
|
x x* |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Ньютона сходится к x* |
с квадратичной скоростью. |
|
|
|
|
|||||||||||||||
|
|
Из теоремы 1 следует, что сходимость метода Ньютона доказана лишь |
||||||||||||||||||
для |
|
достаточно |
|
хорошего начального приближения |
x0 . |
Условие |
||||||||||||||
q |
|
R |
|
|
f ( x0 ) |
|
|
|
1, |
гарантирующее |
сходимость для |
заданного x0 , |
||||||||
|
|
|
|
|
||||||||||||||||
2r 2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
труднопроверяемо, т.к фигурирующие в нем константы, как правило,
неизвестны. Сложность отыскания нужного x0 – недостаток метода Ньютона. Еще более существенным недостатком является высокая трудоемкость метода, обусловленная необходимостью вычисления и обращения на каждом шаге f ( xk ). Следовательно, применение классического метода Ньютона далеко не всегда приводит к успеху. Многочисленные модификации направлены на то, чтобы, сохраняя основные достоинства метода Ньютона – его быструю сходимость, уменьшить трудоемкость и ослабить требования на выбор x0 . Тем не менее, метод Ньютона считается эталоном, с которым надо сравнивать другие алгоритмы.
8
