2.3 Ряд динамики расхода кормов на одну корову и его характеристика
Ряд динамики представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение общественных явлений во времени[3, стр. 107].
Для изучения интенсивности изменения уровней ряда во времени исчисляются аналитические показатели, расчет которых представлен в таблице 6.
По данным таблицы 6 наглядно видно, что средний уровень затрат кормов на 1 корову ц к. ед. за год (2005 - 2012) составил 50,23 ц к. ед., а средний абсолютный прирост -0,74 ц к. ед. на 1 голову. Темп роста составил 99% , а темп прироста -1%. В данной динамике четко прослеживается тенденция снижения затрат корма на 1 корову.
Наибольшее снижение произошло в 2012 году. Наибольшие затраты корма на 1 корову наблюдалось в 2005 году, тогда как с каждым годом это количество все уменьшалось.
Важное значение в анализе динамических рядов имеют приемы выявления общей тенденции. Выявить тенденцию (тренд) означает любыми методами устранить случайные и выявить необходимые факторы. Существует несколько таких приемов, некоторые из них рассчитаны с помощью таблицы 7.
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 6 |
|||||||||||
Аналитические показатели ряда динамики. |
||||||||||||||||||||||||
Год |
Средние затраты корма на одну корову, ц к. ед. |
Абсолютный прирост, ц к. ед. на 1 голову |
Коэффициент роста |
Коэффициент прироста |
Темп роста, % |
Темп прироста, % |
Абсолютное значение одного процента прироста, ц к. ед. на 1 голову |
Процентн.пункты (роста, снижения),% |
||||||||||||||||
базисный |
цепной |
базисный |
цепной |
базисный |
цепной |
базисный |
цепной |
базисный |
цепной |
базисный |
цепной |
|||||||||||||
2005 |
55,39 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
||||||||||
2006 |
54,82 |
-0,57 |
-0,57 |
0,99 |
0,99 |
-0,01 |
-0,01 |
98,97 |
98,97 |
-1,03 |
-1,03 |
0,55 |
- |
- |
||||||||||
2007 |
54,11 |
-1,28 |
-0,71 |
0,98 |
0,99 |
-0,02 |
-0,01 |
97,69 |
98,70 |
-2,31 |
-1,30 |
0,55 |
-1,28 |
-0,27 |
||||||||||
2008 |
53,55 |
-1,84 |
-0,56 |
0,97 |
0,99 |
-0,03 |
-0,01 |
96,68 |
98,97 |
-3,32 |
-1,03 |
0,54 |
-2,29 |
0,26 |
||||||||||
2009 |
52,80 |
-2,59 |
-0,75 |
0,95 |
0,99 |
-0,05 |
-0,01 |
95,32 |
98,60 |
-4,68 |
-1,40 |
0,54 |
-3,65 |
-0,37 |
||||||||||
2010 |
52,50 |
-2,89 |
-0,30 |
0,95 |
0,99 |
-0,05 |
-0,01 |
94,78 |
99,43 |
-5,22 |
-0,57 |
0,53 |
-4,19 |
0,83 |
||||||||||
2011 |
50,97 |
-4,42 |
-1,53 |
0,92 |
0,97 |
-0,08 |
-0,03 |
92,02 |
97,09 |
-7,98 |
-2,91 |
0,53 |
-6,95 |
-2,35 |
||||||||||
2012 |
50,23 |
-5,16 |
-0,74 |
0,91 |
0,99 |
-0,09 |
-0,01 |
90,68 |
98,55 |
-9,32 |
-1,45 |
0,51 |
-8,29 |
1,46 |
||||||||||
Итого в среднем |
-0,74 |
-0,74 |
0,99 |
0,99 |
-0,01 |
-0,01 |
99,00 |
99,00 |
-1,00 |
-1,00 |
0,53 |
- |
- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 7 |
|||||||||||||||||
Методы обработки динамики затрат корма на одну корову для выявления основной тенденции |
||||||||||||||||||||||||||||||||
Год |
Средние затраты корма на одну корову, ц к. ед. |
Первые разности |
Вторые разности |
Метод укрупнения периодов (3–х лт.) |
Метод средней скользящей (3-х лт.) |
Метод аналитического выравнивания по уравнению прямой, вида y(t)=a0±a1t |
Метод аналитического выравнивания по уравнению параболы, вида y(t)=a0±a1t±a2t2 |
|||||||||||||||||||||||||
Ʃ |
yср |
Ʃ |
yср |
t |
t2 |
yt |
|
|
t4 |
yt2 |
|
|
||||||||||||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
||||||||||||||||
2005 |
55,39 |
- |
- |
- |
- |
- |
- |
-7 |
49 |
-387,73 |
55,57 |
0,0324 |
2401 |
2714,11 |
56,24 |
0,71 |
||||||||||||||||
2006 |
54,82 |
-0,57 |
- |
164,32 |
54,77 |
164,32 |
54,77 |
-5 |
25 |
-274,10 |
54,85 |
0,0009 |
625 |
1370,50 |
55,29 |
0,22 |
||||||||||||||||
2007 |
54,11 |
-0,71 |
-0,14 |
- |
- |
162,48 |
54,16 |
-3 |
9 |
-162,33 |
54,13 |
0,0004 |
81 |
486,99 |
54,42 |
0,09 |
||||||||||||||||
2008 |
53,55 |
-0,56 |
0,15 |
- |
- |
160,46 |
53,49 |
-1 |
1 |
-53,55 |
53,41 |
0,0196 |
1 |
53,55 |
53,62 |
0,00 |
||||||||||||||||
2009 |
52,80 |
-0,75 |
-0,19 |
158,85 |
52,95 |
158,85 |
52,95 |
1 |
1 |
52,80 |
52,69 |
0,0121 |
1 |
52,80 |
52,90 |
0,01 |
||||||||||||||||
2010 |
52,50 |
-0,30 |
0,45 |
- |
- |
156,27 |
52,09 |
3 |
9 |
157,50 |
51,97 |
0,2809 |
81 |
472,50 |
52,26 |
0,06 |
||||||||||||||||
2011 |
50,97 |
-1,53 |
-1,23 |
- |
- |
153,70 |
51,23 |
5 |
25 |
254,85 |
51,25 |
0,0784 |
625 |
1274,25 |
51,69 |
0,51 |
||||||||||||||||
2012 |
50,23 |
-0,74 |
0,79 |
- |
- |
- |
- |
7 |
49 |
351,61 |
50,53 |
0,09 |
2401 |
2461,27 |
51,20 |
0,93 |
||||||||||||||||
Итого |
424,37 |
- |
- |
- |
- |
- |
- |
0 |
168 |
-60,95 |
424,40 |
0,5147 |
6216 |
8885,97 |
427,60 |
2,55 |
||||||||||||||||
Продолжение таблицы 7
Метод
аналитического выравнивания по
уравнению гиперболы, вида
|
||||
1/t |
1/t2 |
y/t |
|
|
18 |
19 |
20 |
21 |
22 |
-0,143 |
0,020 |
-7,913 |
53,193 |
4,827 |
-0,200 |
0,040 |
-10,964 |
53,250 |
2,465 |
-0,333 |
0,111 |
-18,037 |
53,383 |
0,528 |
-1,000 |
1,000 |
-53,550 |
54,050 |
0,250 |
1,000 |
1,000 |
52,800 |
52,050 |
0,563 |
0,333 |
0,111 |
17,500 |
52,717 |
0,047 |
0,200 |
0,040 |
10,194 |
52,850 |
3,534 |
0,143 |
0,020 |
7,176 |
52,907 |
7,167 |
0,000 |
2,343 |
-2,794 |
424,400 |
19,381 |
На основании ряда динамики затрат кормов на одну корову, для выявления общей тенденции использованы наиболее часто используемые методы: укрупнения периодов, средней скользящей, аналитического выравнивания.
Первые методы не позволяют выявить общую тенденцию (тренд) в данном динамическом ряду, поэтому наиболее прогрессивным методом является метод аналитического выравнивания.
Выявим модель тренда (уравнение прямой) для определения тенденции.
,
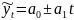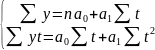
В нашем случае:
=>
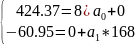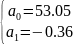
Значит модель тренда (уравнение прямой)
для определения тенденции имеет следующий
вид:
.
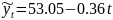Из данного уравнения тренда наглядно видно, что в среднем за год затраты корма на 1 корову снижаются на 0.36 ц к. ед..
Ошибка аппроксимации составляет 0.29 ц к. ед., коэффициент вариации 0.55%:
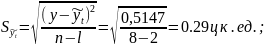
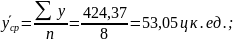
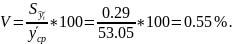
Выявим модель тренда (уравнение параболы) для определения тенденции.
,
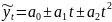В нашем случае:
=>
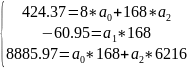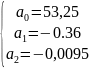
Значит модель тренда (уравнение
параболы) для определения тенденции
будет иметь следующий ви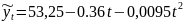д:
.
Из данного уравнения тренда наглядно
видно, что в среднем за год затраты корма
на 1 корову снижаются на 0.36 ц к. ед..
Ошибка аппроксимации составляет 0,65 ц к. ед., коэффициент вариации 1,22%.
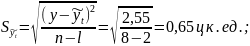
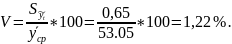
Выявим модель тренда (уравнение гиперболы) для определения тенденции.
,
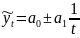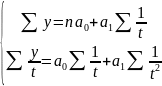
В нашем случае:
=>
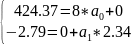Значит модель тренда (уравнение гиперболы)
для определения тенденции имеет следующий
вид:
.
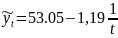Из данного уравнения тренда наглядно видно, что в среднем за год затраты корма на 1 корову снижаются на 1,19 ц к. ед..
Ошибка аппроксимации составляет 1,78 ц к. ед., коэффициент вариации 3,39%:
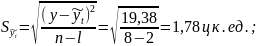
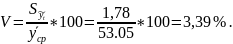
Прямая лучше отражает тенденцию развития явления во времени, т.к. ошибка аппроксимации меньше.
Так как коэффициент вариации не превышает 25%, следовательно данный динамический ряд устойчив и данную модель тренда можно использовать при прогнозировании.
Уравнение тренда применяют при прогнозировании, т.е. определения уровней ряда динамики за его пределами – метод экстраполяции. Экстраполяция – нахождение уровней за пределами изучаемого ряда, т.е. продление будущее тенденции, наблюдавшееся в прошлом[3, стр. 140].
Период прогнозирования не должен превышать 1/3 числа уровней, на основе который построено уравнение тренда.
Точечный прогноз:
Для 2013 г. -
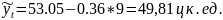
Для 2014 г. -
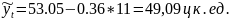
Интервальный прогноз осуществляется по формуле:
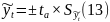
Среднее квадратическое отклонение от тренда (ошибка аппроксимации):
Теоретический уровень исчисляется так:
Для 2013 г. -
;
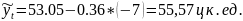Для 2014 г. -
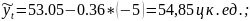
Р = 0,99, St
=0,994, k =n-1=8-1=7,
=>
Интервальный прогноз:
Для 2013 г.:
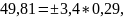
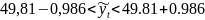
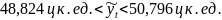
Для 2014 г.:
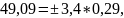
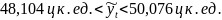
Значит интервальный прогноз для затрат кормов на 1 корову для 2013 г 49,81 ц к. ед. находится в пределах от 48,82 ц к. ед. до 50,80 ц к. ед. А для 2014 г интервальный прогноз для затрат кормов на 1 корову 49,09 ц к. ед. находится в пределах от 48,10 ц к. ед. до 50,08 ц к. ед..
Прогнозирование затрат кормов на 1 корову можно производить также при помощи полиномиальной функции различных порядков, экспоненциальной функции и степенной функции.
Строится график зависимости между временным периодом и затратами корма на 1 корову, проводится линия тренда и на ее основании составляется прогноз.