5.1.5. Потери в магнитном материале в переменном магнитном поле

В переменном магнитном поле в магнитном материале имеют место потери на перемагничивание (на гистерезис) и на вихревые токи. Потери на гистерезис зависят от площади статической петли гистерезиса и частоты поля. При перемагничивании материала с частотой мощность потерь на гистерезис на единицу массы определится следующим образом, Вт/кг:

,

где – плотность материала, кг/м³;

– частота, Гц.

Для расчёта удельных потерь на гистерезис предложена эмпирическая формула, Вт/кг:

,

где – коэффициент, зависящий от материала;

и зависит от материала;

– амплитуда индукции, Тл.

Потери на вихревые токи зависят не только от магнитных, но и от электрических свойств материала и от формы сердечника. Для листового образца удельные потери на вихревые токи определяются следующим образом, Вт/кг:

,

где – амплитуда индукции, Тл;

– толщина листа, м;

– удельное сопротивление, Ом м;

– плотность, кг/м³;

– частота, Гц.

Из-за вихревых токов напряжённость магнитного поля по толщине пластины магнитопровода будет не одинаковой, наибольшая напряжённость будет находиться на поверхности, наименьшая – по центру пластины. Глубина проникновения магнитного поля в пластину (глубина на которой магнитное поле ослабляется в раза) определяется по формуле:

, м,

где – угловая частота.

При использовании ферромагнитного материала в переменном магнитном поле величина индукции и напряжённости поля связаны динамической петлёй гистерезиса и динамической кривой намагничивания, которую проводят по вершинам динамических петель гистерезиса. При синусоидальном изменении В изменение не синусоидальное и наоборот из-за нелинейности зависимости .

Для характеристики магнитных потерь используют понятие комплексной магнитной проницаемости и тангенса угла магнитных потерь. Это можно пояснить на примере катушки на тороидальном ферромагнитном сердечнике (рис. 5.7). Катушку на сердечнике при питании от источника переменного напряжения можно представить следующей схемой замещения:

Рис. 5.7. Схема замещения катушки с сердечником: – сопротивление провода катушки, обычно ; – эквивалентное сопротивление, электрические потери в котором равны потерям в стали сердечника; ; – потери в сердечнике; – индуктивность катушки без ферромагнитного сердечника; – индуктивность катушки с ферромагнитным сердечником

Без учёта сопротивления провода катушки полное эквивалентное сопротивление катушки:

,

где – комплексная магнитная проницаемость;

– реактивная составляющая магнитной проницаемости, учитывающая потери в магнитопроводе.

Потери в сердечнике характеризуются тангенсом угла магнитных потерь:

.

Векторная диаграмма тока и напряжений для катушки с ферромагнитным сердечником с учётом потерь в сердечнике показана на рис. 5.8.

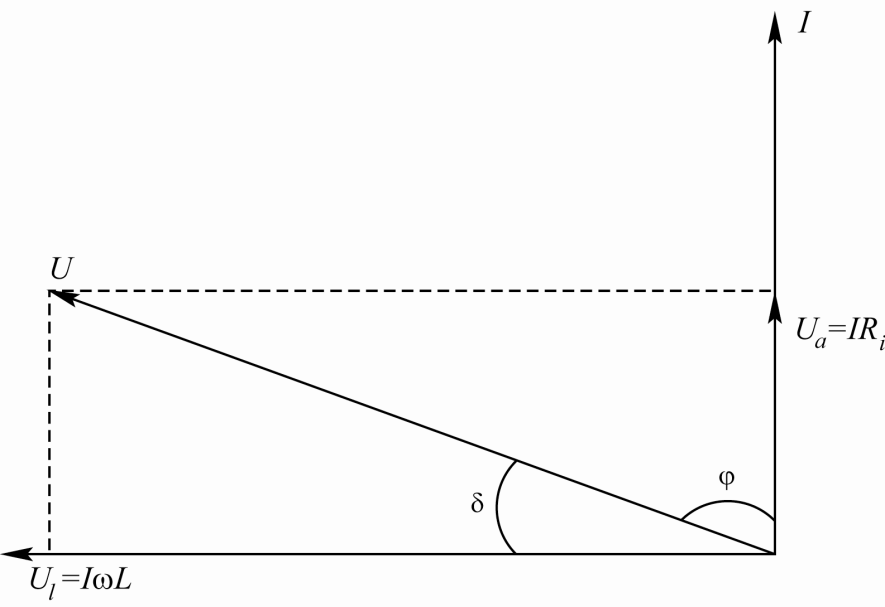
Рис. 5.8. Векторная диаграмма тока и напряжений

5.2. Экспериментальное определение кривой намагничивания магнитных сердечников

Проще всего кривая намагничивания сердечника снимается на переменном токе. Для этого на сердечник наматывают две обмотки: питания и измерительную (рис. 5.9). На обмотку питания W₁ подаётся синусоидальное напряжение частотой f последовательно с обмоткой включен амперметр. К измерительной обмотке подключен вольтметр.

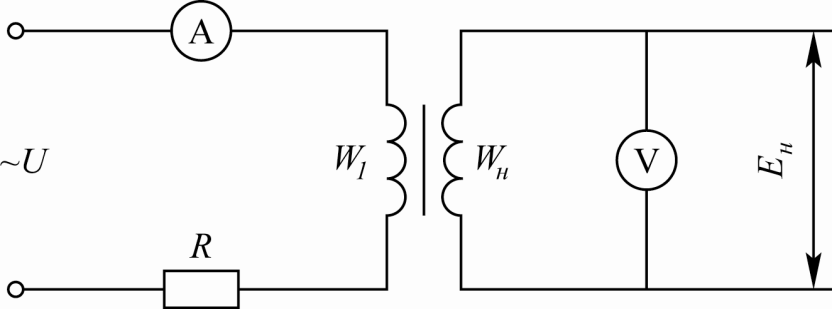
Рис. 5.9. Схема для определения кривой намагничивания сердечника

Н_m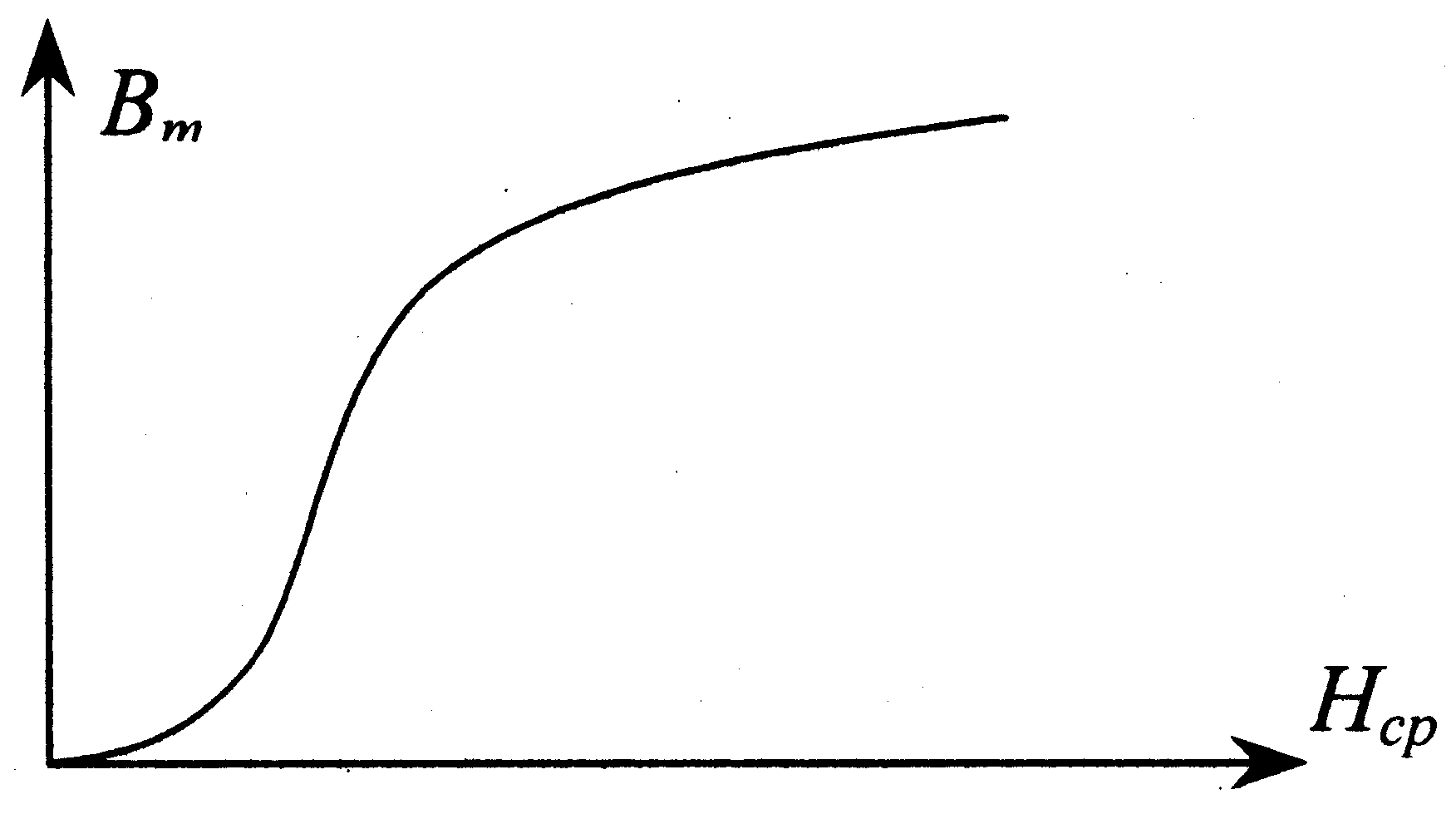

Рис. 5.10. Кривая намагничивания, снятая на переменном токе

При синусоидальном напряжении на обмотке индукция в сердечнике тоже будет изменяться по синусоиде, а ток в обмотке будет несинусоидальным. По показателям вентильного вольтметра можно определить амплитудное значение индукции в сердечнике:

, (5.12)

где – число витков измерительной обмотки;

– активное сечение магнитопровода.

По показаниям амперметра определяется среднее значение напряжённости магнитного поля:

, (5.13)

где – число витков обмотки питания;

– средняя длина силовой линии сердечника.

Так как ток несинусоидален, его следует измерять прибором вентильного типа. Его показания пропорциональны среднему значению тока, однако проградуирован он обычно в действующих значениях эквивалентной синусоиды. В этом случае его показания перед подстановкой в формулу надо умножить на величину, обратную коэффициенту формы синусоиды . То же касается показаний вольтметра .

Кривая намагничивания, построенная по формулам (5.12) и (5.13), отличается от основной кривой намагничивания. Однако для многих магнитомягких материалов это различие невелико. Поэтому полученную кривую намагничивания можно использовать для расчётов электромагнитных устройств, для сравнения свойств различных сердечников.