§ 4 Растяжения с изгибом

Пусть на стержень действует только продольная сила N, несущая способность будет обеспечена если:

Пусть действует только изгибающий момент М, несущая способность будет обеспеченна если:

п ри совместном действии N и М, несущая способность обеспеченна если:

п еремножим все согласные на R_p и получим формулу СНиП:

Формула справедлива при любых соотношениях N и М и даёт погрешность в запас прочности до 20%.

§ 5 Сжатие с изгибом для балок или для стержней с изгибной жесткостью.

Аналогично разделу § 4 получим:

Перемножим все слагаемые на R_C = Ru и получим:

погрешность в запас до 6%.

§ 6 Сжатие с изгибом для стержней

Р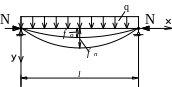 ассмотрим шарнирно опёртый стержень под действием нагрузки q:

f₀ – максимальный прогиб.

К стержню в деформированном состоянии приложим продольную силу N.

Ось стержня получит дополнительное перемещение, максимальный прогиб – f_n . Пусть изогнутая ось стержня будет синусоидой при действии только нагрузки q, а также при совместном действии q и N.

(1)

Задача решается в рядах Фурье, но с использованием только первого члена ряда. Полный момент от действия q и N будет равен:

(2) M_nx = M_qx + N × f_nx – учёт деформированной оси.

Дифференцированное уравнение изогнутой оси балки:

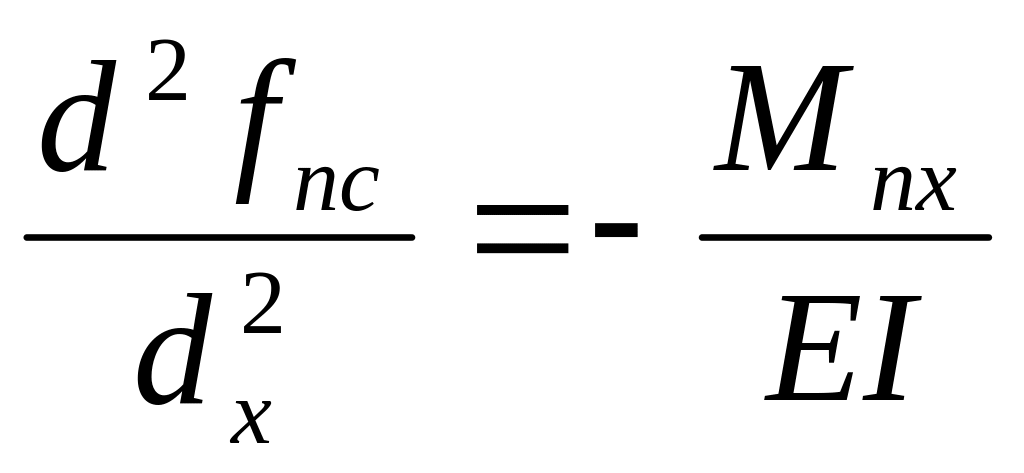
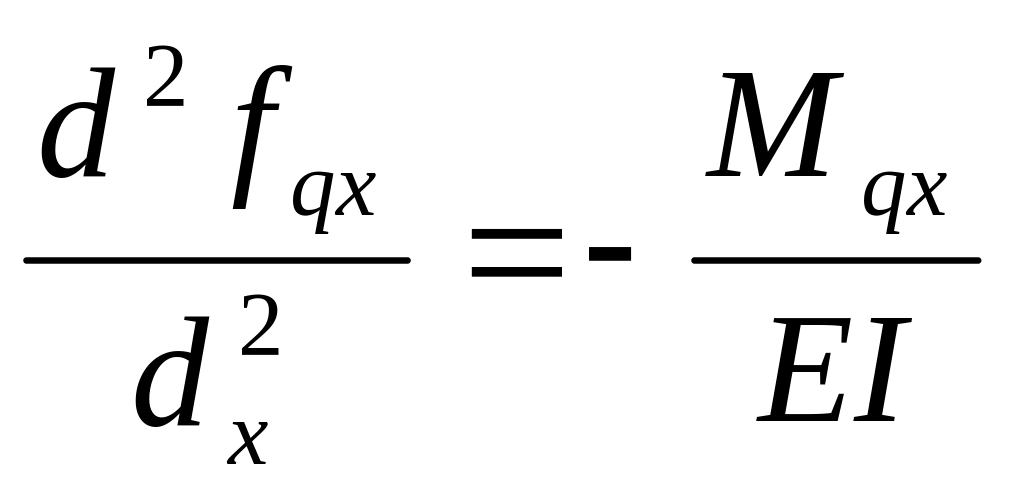(3)

Разделим все слагаемые уравнения (2) на EI

(4)

Заменим все слагаемые их частными производные:

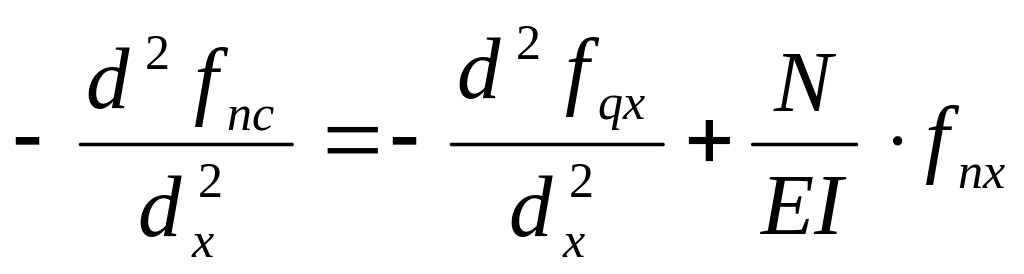(5)

Продифференцируем выражение (1) два раза и запишем в формулу (5)

(6)

С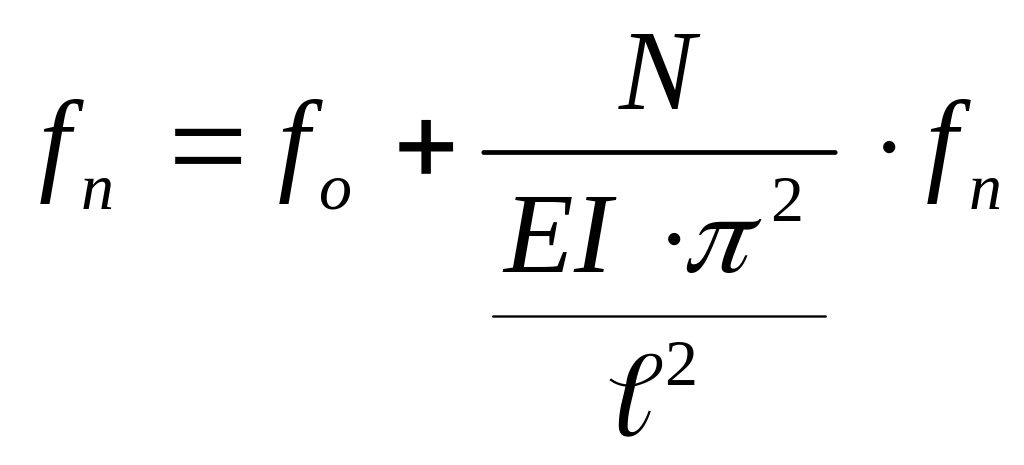 ократим sin ; разделим все слагаемые в формуле (6) на

(7)

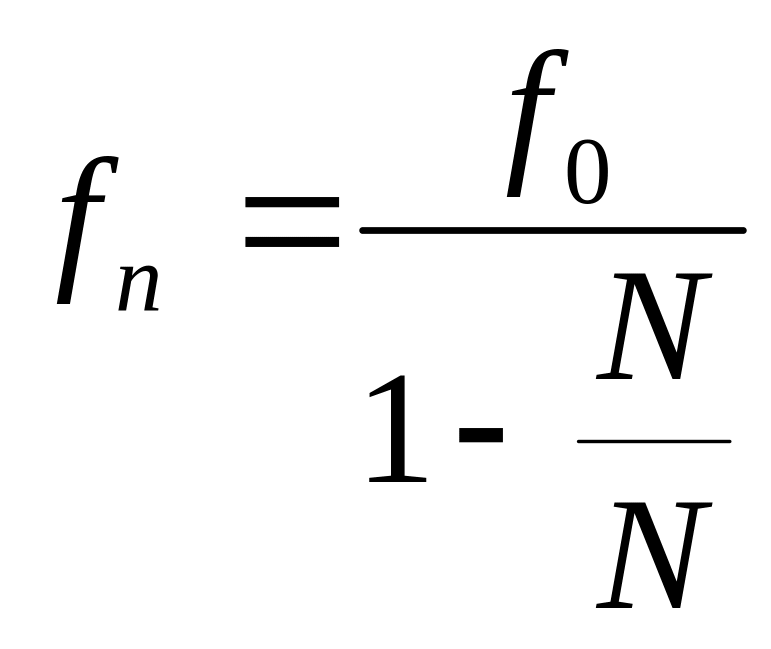
(8)

- Эйлерова критическая сила

В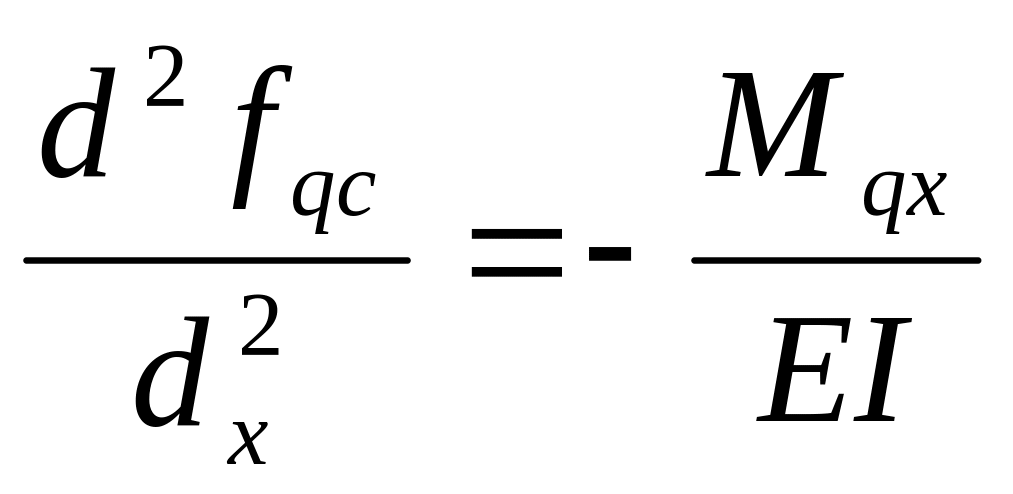 ыразим f₀ через M и N, для этого запишем:

(9)

(10)

Поставим значение f_n=f₀/_ξ; ; в формулу (2) и после простых преобразований (11)

ξ - учитывает увеличение изгибающего момента или увеличение прогиба за счет деформации оси стержня при совместном действии q и N.

(12) перерезывающая сила.

Расчётная формула при сжатии с изгибом деревянного стержня:

С НиП (13)

Ограничения для ξ

1) 0< ξ <1

;

ξ – получено правильно только для упругой работы материала (при λ > 70)

При λ < 70определяется ξ приближённо.

Приступая к расчету, можем задаться малой площадью А и получим большое λ, так, что слагаемое , а ξ станет «–» - отрицательным, что не имеет физического смысла. В этом случае увеличиваем А, пока ξ станет > 0.

2) если доля изгиба очень мала , то требуется дополнительная проверка по формуле центрально-сжатого стержня, (например для безмоментной арки)

3 ) Если нагрузка отличается от плавной (распределённой или синусоидной), например в виде сосредоточенных сил или моментов , тогда ξ = ξ × К_н , К_н- поправочный коэффициент в СНиПе.

4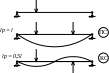 ) При действии произвольной нагрузки поперечной раскладываем нагрузку на

прямосиметричную и кососиметричную.

М_деф – момент с учетом деформированной схемы.

Формула (13) – это формула прочности, мы имеем напряжение краевые с учетом деформируемой схемы. По этой формуле проверяют прочность рам, куполов, арок, верхних поясов ферм и т.д., но она сделана только для упругой работы стержня.