Матрица выборов.

		Кого выбирают.											В>
Кто выбирает		А	Б	В	Г	Д	Е	Ж	З	И		К	В>	K·В>
	А			(3)	0,5	2	(1)		0,5	( )			5	7
	Б	1			(2)	3	( )						3	6
	В	(1)	0,5		3	2			0,5				5	7
	Г		(3)				1	(0,5)	2		(0,5)		5	7
	Д	3			2				0,5		1		4	6,5
	Е	3	(1)		(2)				0,5		0,5		5	7
	Ж				3								1	3
	З	1	0,5	0,5	3		0,5				(2)		6	7,5
	И	3											1	3
	К				(3)	1	2		0,5				4	6,5
 В’  	В<	6	4	2	8	4	4	1	6	0		4	39	60,5
	K·B<	12	5	3,5	18,5	8	4,5	0,5	4,5	0		4	60,5
	В//	4	1	2	5	2	4	1	3	0		3	25
	B*	1	2	1	3	0	1	1	0	1		1	11

Статистическая обработка данных должна учитывать ассиметричность получаемой кривой распределения. Опыт показывает, что больше всего такая кривая приближается к биноминальному распределению. Поэтому способ статистической обработки здесь основан на формулах биноминального закона распределения. Этот способ обработки материала позволяет установить (с определенной вероятностью допустимой ошибки) границы доверительного интервала как для выборов, так и для отклонений, то есть определить, например, сколько выборов /отклонений/ должно получить данное лицо, чтобы считаться «популярным» /непопулярным/ в группе. При обработке результатов обычно используют три вероятности допустимой ошибки р = 0,05; 0,01; 0,001. В практикуме достаточным уровнем допустимой ошибки является р = 0,05.

Для установления статистически обоснованных доверительных границ – минимального и максимального количества выборов (Хмин. и Хмакс.), за пределами которых, при заданной вероятности допустимой ошибки, индивиды могут считаться «популярными» или «непопулярными» в группе, производятся следующие статистические расчеты.

Границы доверительного интервала вычисляются по следующей формуле¹:

х = х + tδ , где

х – выборочное среднее х = М/(N-1), где

М – общее количество(сумма) выборов, сделанных всеми членами группы (с учетом коэффициента(в*к) и без учета к);

N – число членов группы;

δ – выборочная дисперсия δ = n · p · q где n=N-1

p – оценка вероятности быть избранным; p = х / N – 1

q – оценка вероятности не быть избранным; q = 1 - p

t – коэффициент, учитывающий ассиметричность распределения. Он определяется по таблице Сальвоса (см. таблицу 2). Для соответствующей степени ассиметричности а₃ и заданной вероятности допустимой ошибки p = 0,05; 0,01; 0,001. ( cм. Bastin, 1961)

Таблица 2.

КРИТИЧЕСКИЕ ЗНАЧЕНИЯ по Сальвосу.

Степень ассиметричности	Р 0,05	Р 0,01	Р 0,001	Степень ассиметричности	Р 0,05	Р 0,01	Р 0,001
0,0	-1,64	-2,33	-3,09	0,0	1,64	2,33	3,09
0,1	-1,62	-2,25	-2,95	0,1	1,67	2,40	3,23
0,2	-1,59	-2,18	-2,81	0,2	1,70	2,47	3,38
0,3	-1,56	-2,10	-2,67	0,3	1,73	2,54	3,52
0,4	-1,52	-2,03	-2,53	0,4	1,75	2,62	3,67
0,5	-1,49	-1,95	-2,40	0,5	1,77	2,69	3,81
0,6	-1,46	-1,88	-2,27	0,6	1,80	1,76	3,96
0,7	-1,42	-1,81	-2,14	0,7	1,82	2,83	4,10
0,8	-1,39	-1,73	-2,02	0,8	1,84	2,89	4,24
0,9	-1,35	-1,66	-1,90	0,9	1,86	2,96	4,39
1,0	-1,32	-1,59	-1,79	1,0	1,88	3,02	4,53
1,1	-1,28	-1,52	-1,68	1,1	1,89	3,09	4,67

Левая сторона этой таблицы соответствует левой половине кривой распределения (Хмин), а правая – правой половине (Хмакс), поэтому при нахождении Хмин (нижней границы доверительного интервала) следует пользоваться левой стороной таблицы, а при нахождении Хмакс (верхней границы доверительного интервала) правой ее стороной.

Проиллюстрируем производимые расчеты на примере. Предположим, что при социометрическом исследовании некоторой гипотетической группы, число членов которой (N) составляет 31, а общее количество сделанных выборов – 150 (М).

С реднее количество выборов, приходящихся в этой группе на одного человека:

Х = 150/30 = 5.

Оценка вероятности быть избранным в данной группе:

р = 5/30  0,17, а вероятность не быть избранным

q = 1 – 0,17 = 0,83

Оценка стандартного отклонения δ = (30·0,17·0,83) = 2,0

Степень ассиметричности: а₃ =  0,33

По таблице Сальвоса для р 0,05 находим tмин = -1,56

tмакс=1,73; Хмин = 5 – 1,56·2,1 = 1,7; Хмакс = 5 + 1,73·2,1 = 8,6

Таким образом, при вероятности допустимой ошибки р 0,05 членов нашей гипотетической группы, получивших менее 1,7 выбора (округленно один и менее 1-го выбора), можно считать «непопулярными», а членов группы, получивших более 8,6  ( 9 выборов) считать «популярными» в данной группе. Остальные составляют группу «средних».

СОЦИОГРАММЫ

Социограммы позволяют графически, наглядно представить структуру отношений в группе, выделить подгруппы «популярных», «средних», «непопулярных», «отвергаемых» индивидов, выделить лидера из группы «популярных». Социограмма позволяет сделать предположение о стиле лидерства, судить о сплоченности, организованности группы, и отчасти о ее психологическом климате.

Социограммы бывают групповые и индивидуальные.

При построении социограммы используют следующие обозначения:

А Б выбор (А выбирает Б)

А Б взаимный выбор или А ═══ В

А Б ожидаемый выбор (А ожидает получить выбор от Б)

А Б отклонение (А ожидает отклонение от Б)

А Б взаимное отклонение

А Б ожидаемое отклонение (А ожидает от Б отклонение)

А >< Б А выбирает Б и ожидает получить выбор от Б

Для различения пола членов группы обозначают:

 мужчина

 женщина

  члены группы, отсутствующие при проведении исследований.

Обычно же на социограмме члена группы обозначают кружком, или квадратом, в котором вписывается его номер из группового списка.

Рис. 1. СОЦИОГРАММА ПЕРВЫХ ДВУХ ВЫБОРОВ

(р 0,05)

А,Б,С - подгруппы.

А

Б

С

Коллективная социограмма. Различают два типа социограмм. Во-первых, в созданных Морено социограммах, популярные члены помещались в центр, а непопулярные – на периферию; исследователь при этом старался отобразить все связи, объединяющие субъектов, выделить типичные конфигурации взаимоотношений: цепи, треугольники, квадраты и т.д. Этот способ отображения групповых взаимоотношений обладал большими недостатками: существовала известная произвольность в относительном положении субъектов, возникали известные трудности графического изображения связей между субъектами, когда численность группы достигала двадцати и более человек, сети связей становились практически неразличимы. Для улучшения читабельности социограммы, в настоящее время, обычно, ограничиваются отображением связей одного порядка: либо выборов, либо отклонений. Прилагались многочисленные усилия, чтобы стандартизировать и рационализировать построение социограммы. Одной из наиболее интересных попыток явилась «социограмма-мишень», предложенная исследовательницей Нортвей в 1952 г. При ее построении учитывалось разделение группы на «популярных», «средних» и «непопулярных» членов группы. Испытуемые, входящие в группу «популярных», помещались при этом в центр нескольких концентрических кругов (рис.2), «непопулярные» – в наружное кольцо, «средние» – во внутреннее кольцо. Можно также использовать различные части социограммы-мишени, концентрируя членов группы в зависимости, например, от пола, возраста и т.д.

Техника «социограммы-мишени» представляет таким образом некоторый прогресс, не решая, однако, всех трудностей. Так, например, она не может стандартизировать относительное расположение субъектов внутри концентрических зон; группа «средних» индивидов при этом остается недифференцированной. Кроме этого, в случае больших групп и многочисленных выборов приходится ограничиваться обозначением лишь небольшой части связей, чаще всего первого выбора ,первых трех выборов или взаимных связей, чтобы достичь необходимой ясности графического изображения (см. рис. 3). Хорошо выполненной социограммой является такая социограмма, где отсутствуют или они сведены к минимуму пересекающиеся выборы. Прорисовывание социограммы – это кропотливая работа, требующая терпения и упорства, напоминает процедуру распутывания клубка нитей – связей….

Рис. 2. СОЦИОГРММА ПЕРВОГО ВЫБОРА

(внутри – популярные, снаружи – непопулярные)

4 ═══════ 5 - взаимный выбор

Комментарий: Социограмма демонстрирует, что группа разбита на подгруппы достаточно изолированные друг от друга. Среди популярных фигура лидера отсутствует. Типичная социограмма студенческой группы на 1 курсе.

Рис. 3 СОЦИОГРАММА ВЗАИМНЫХ ОТКЛОНЕНИЙ

(в центре – наиболее отвергаемые, снаружи – наименее отвергаемые).

Обычно составляют несколько коллективных социограмм для одной группы: социограммы взаимных выборов, взаимных отклонений, первого выбора, первых трех (пяти) выборов и некоторые другие (в зависимости от интересов исследователя).

При анализе коллективных социограмм можно выделить следующие типичные подструктуры (рис. 4).

Рис. 4.

Типичные схемы (структуры) внутригрупповых отношений между членами группы: а) колесо или звезда; б) цепь; в) круг; г) триада; д) расцепленная цепь; е) тетрады (ядра).

а б в

д г е

Изучение проблем группового принятия решения показало преимущество той или иной структурной организации группы в зависимости от типа задач, предлагаемых группе для решения. Большой интерес в социометрическом исследовании представляют «ядра», имеющие замкнутую структуру. Это как бы «группы в группах» со своими интересами, нормами, со своей субкультурой. В организациях ядра часто встречаются в отделах «охраны и безопасности», но не только….

Индивидуальные социограммы. Существуют различные виды индивидуальных социограмм, позволяющих произвести более тонкий анализ положения конкретного члена в группе.

Наиболее простой способ построения индивидуальной социограммы заключается в том, что субъект, чьи связи исследуются, располагается в центре, наподобие атома, к которому сходятся связи с теми, кто его выбрал, отверг и т.д. Индивиды, имеющие социометрические связи с данным субъектом, располагаются вокруг него, на расстоянии, пропорциональном порядку полученного выбора. Можно отдельно построить социограмму полученных выборов (социоцентрическая позиция индивида) и социограмму сделанных выборов ( эгоцентрическая позиция индивида ).

Социограмма лидера. Индивидуальная социограмма помогает, например, отличить позицию лидера от позиции «популярного» члена группы.

Довольно распространенным является следующее социометрическое определение лидера – это индивид, получивший максимальное количество выборов при различных социометрических критериях. Однако на практике нередко встречаются случаи, когда среди группы «популярных» мы не можем четко выделить лидера, так как число выборов у каждого члена группы «популярных» может оказаться равным или почти равным. В этих случаях индивидуальные социограммы могут дать важную для решения вопроса информацию. Четкая лидерская позиция среди популярных обнаруживается в том случае, когда сами популярные члены группы отдают предпочтения в своих выборах преимущественно кому-то одному из своего числа. Лидер группы – это прежде всего выбор ее «элиты», т.е. самих популярных.

Рис. 5 Схематическое изображение особенностей стилей лидерства.

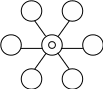
А Б

А – авторитарный стиль

Б – демократический стиль

Основные отличия позиции лидера от популярного члена группы.

1. Лидер остается в зоне популярности при различных критериях выбора и способах подсчета выборов.

2. Лидером можно назвать такого популярного члена группы, которого предпочитают сами популярные.

3. О стиле лидерства можно судить по характеру взаимоотношений тех, кто его выбирает, и в первую очередь по характеру взаимоотношений между популярными.

Индивидуальная социограмма позволяет выделить в группе «непопулярных» – «отверженного» и «изолированного» члена. «Изолированным» называют члена г не имеющего ни выборов, ни отклонений, а «отверженным» – не имеющего выборов или имеющего незначимое их число, но при этом получившего значимо большое число отклонений. В оценке позиции «изолированного» и «отверженного» члена группы очень важно учитывать отношение самого члена группы к своему положению, оценку того, насколько она адекватна. По ответам можно судить о реакции изолированного или отвергаемого члена группы на свое положение в группе. Если индивид не получает выборов, но при этом сам выбирает и ожидает их получить, то это свидетельствует об отсутствии социально-психологической компетентности, данное лицо явно нуждается в социально-психологической помощи.

ИНДЕКСЫ

Социометрические индексы дают количественную оценку положения индивида в группе, а также оценку группы в целом. Их делят на две большие группы: индексы индивидуальные и индексы групповые.

Индивидуальные индексы:

1) Индекс социометрического статуса индивида в группе. Отражает социальное внимание к индивиду со стороны группы.

Обычно, вычисляют не общий индекс, а позитивный или негативный социометрический статус отдельно, т.е.

Индекс социометрического статуса выражает отношение группы к одному из ее членов. При этом важно помнить, что величина статуса задается ситуацией, критерием выбора, в данном случае видом совместной групповой деятельности и может сильно варьировать при разных критериях выборов. Только у харизматических лидеров эта величина имеет тенденцию сохраняться на одном и том же уровне вне зависимости от критерия и способа подсчета.

2) Индекс психологической экспансивности индивида в группе ¹:

Положительная экспансивность Отрицательная экспансивность

Этот индекс характеризует степень активности индивида во взаимодействии с другими индивидами.

3) Индекс социально-психологической компетентности.(Творческая часть задания) С.троится на основе учета ожидаемых выборов , угаданных выборов и взаимных выборов.

Для характеристики положения индивида в группе можно вычислять самые разнообразные индексы, манипулируя данными матрицы, однако, главная сложность состоит в интерпретации полученных результатов, соотнесении их с известными социально-психологическими понятиями. С этой же трудностью мы встречаемся и при интерпретации групповых индексов.

Групповые индексы:

1) Индекс групповой экспансивности¹.

Положительная групповая Отрицательная групповая

экспансивность экспансивность

Индекс групповой экспансивности характеризует тип и интенсивность группового взаимодействия.

2) Индекс интегрированности группы.

И = 1 – ( ), где L – число изолированных членов группы.

Этот индекс характеризует степень включенности членов группы в общение в данном виде совместной деятельности.

В) Индекс «групповой сплоченности»

число взаимных выборов

С_л = число возможных взаимных выборов в группе

Индекс групповой сплоченности получил наибольшее распространение в социометрических исследованиях, однако он до сих пор подвергается острой критике. Сплоченность группы измеряется отношением количества взаимных выборов к количеству возможных взаимных выборов. Однако, как было отмечено некоторыми исследователями, взаимность, измеренная лишь в диаде, совсем еще не говорит о сплоченности группы, так как в принципе группа может состоять из тесно взаимосвязанных пар или триад, изолированных друг от друга, хотя и в этом случае мы будем иметь относительно высокий индекс сплоченности в группе.

Другими авторами были предприняты попытки устранить этот недостаток социометрического индекса сплоченности, учитывающий лишь взаимность выбора в диаде. Интересное решение этой проблемы с помощью понятий и методов теории графов предлагает советский исследователь В.И. Паниотто.

Нельсон и Берри (цит. по Кричевскому Р.Л.) предложили вычислять индекс сплоченности по формуле:

С_п = (N-n_i)/N * n_вз/n_мвз * n_нкл/N

Где N – величина группы

n_i – число членов, не имеющих взаимных выборов

n_вз – число полученных взаимных выборов

n_мвз – число максимально возможных взаимных выборов

n_нкл – величина наибольшей клики или подгруппы, не связанной с другими подгруппами.

Проблема сплоченности является одной из самых острых в социальной психологии, так как ее решение несет большое идеологическое и политическое значение. Все большее число авторов приходит к убеждению о гораздо большей сложности данного понятия, чем это представляется на первый взгляд, и невозможности его операционального определения в рамках одной лишь социометрии (Донцов А.И., 1979 г.).

Аналог корреляционного анализа¹.

Вопросы обычной анкеты являются, по сути, шкалами, в результате опроса респондентов мы получаем значения признаков, измеренные в номинальной, порядковой или метрической шкале. Для анализа связи между признаками, измеренными с помощью тех или иных вопросов, существуют корреляционные методы, применяемые в зависимости от типа использованной шкалы. Специфика социометрических исследований заключается в том, что ответом на социометрический вопрос является не значение признака, а фамилии людей (или символы, заменяющие фамилии). Поэтому ни один из существующих методов корреляционного анализа не применим для анализ связей между социометрическими вопросами, точнее, связи между критериями, положенными в основу вопросов. Для этой цели можно предложить методы, которые выполняют в социометрии ту же функцию, что и корреляционный анализ в социологии.

Пусть А – это вопрос, в ответ на который респондент перечисляет людей, с которыми он находится в отношении Р, а В – это вопрос, в ответ на который респондент

.

РЕЗЮМЕ.

Социометрия является по сути единственным методом.,с помощью которого можно исследовать группу как Целое, как Гештальт. Кроме этого социометрия дает возможность изучать личность в контексте ее положения в конкретной группе или в конкретных группах,членом которых она является. Статистические процедуры,разработанные специально для социометрических исследований,позволяют проводить сравнительные исследования разных групп по широкому кругу задач(благополучия-неблагополучия климата,уровня развития группы , ценностных ориентаций группы,для оценки явлений социатрии) ,а также позволяет изучать личность с позиции групповой принадлежности.Данный практикум затрагивает освоение основных социометрических процедур, но при этом дает возможность увидеть перспективность данного метода в решении многих других исследовательских задач.