10.3 Умножитель частоты.

Необходимость в умножителях частоты возникает при разработке высокостабильных источников гармонических колебаний повышенной частоты, когда непосредственное генерирование сигналов такого диапазона затруднительно. Множитель частоты – это устройство, повышающее частоту входного сигнала в n раз, где n – целое число - коэффициент умножения .

Упрощенная электрическая схема умножителя частоты на биполярном транзисторе приведена на рис.10.4., к входу которого последовательно подключены источники гармонического колебания и постоянное напряжение смещения , а резонансный контур на требуемую частоту усиливаемого сигнала.

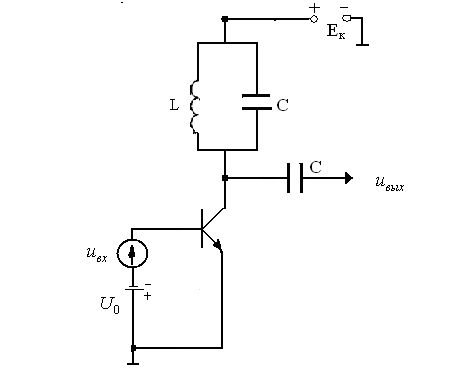
Рис.10.4

10.4 Модулированные колебания и их спектры.

Под модуляцией в радиоэлектронике понимается процесс, при котором один или несколько параметров несущего колебания изменяется по закону передаваемого сообщения. Получаемые в процессе модуляции колебания называют радиосигналами. В аналоговых системах связи радиосигналы передаются непрерывно во времени, и при модуляции могут изменяться амплитуда, частота или фаза несущего гармонического колебания. В зависимости от того, какой из названных параметров несущего гармонического колебания подвергается изменению, различают два основных аналоговой модуляции: амплитудную и угловую. Последний вид модуляции, в свою очередь, подразделяют на частотную и фазовую модуляцию.

В современных цифровых системах связи, радиолокации, радиотелеуправления, радионавигации применяются различные виды импульсной модуляции, при которой радиосигналы представляются в виде так называемых радиоимпульсов.

Радиосигналы с амплитудной модуляцией. В процессе осуществления амплитудной модуляции несущего колебания

(10.16)

его амплитуда должна изменяться по закону:

(10.17)

где - амплитуда в отсутствие модуляции; - угловая частота; - начальная фаза; - полная (текущая или мгновенная фаза); - безразмерный коэффициент пропорциональности; - модулирующий сигнал.

Подставив формулу (10.17) в (10.16), получим общее выражение для АМ-сигнала

(10.18)

Обратимся к простейшему виду амплитудной модуляции – однотональной, когда модулирующий сигнал представляет собой гармоническое колебание

(10.19)

где - амплитуда; - круговая частота; - период; - начальная фаза.

Для упрощения выкладок примем начальные фазы несущего колебания и модулирующего сигнала и . Тогда, подставив формулу (10.19) в (10.18), получим выражение для АМ-сигнала:

(10.20)

Обозначив через максимальное отклонение амплитуды АМ-сигнала от амплитуды несущей и, проведя несложные преобразования, запишем

(10.21)

где - коэффициент или глубина амплитудной модуляции.

Спектр АМ-сигнала. Используя в выражении (10.21) тригонометрическую формулу произведения косинусов, получим

(10.22)

Из формулы (10.22) видно, что при однотональной модуляции спектр АМ-сигнала состоит из трех высокочастотных составляющих. Первая из них представляет собой исходное несущее колебание с амплитудой и частотой . Вторая и третья составляющие характеризуют новые гармонические колебания, появляющиеся в процессе амплитудной модуляции и отражающие передаваемый сигнал.

Колебания с частотами и называются соответственно верхней и нижней боковыми составляющим . Амплитуды боковых составляющих одинаковы, равны и расположены симметрично относительно несущей частоты сигнала . Ширина спектра АМ-сигнала при однотональной модуляции где F-циклическая частота модуляции. Графики несущего колебания с φ₀=90⁰, модулирующего сигнала с θ=90⁰ и АМ-сигнала показаны на рис.10.5 а), б), в), а на рис.10.6 г…е - соответствующие им спектры. При отсутствии модуляции (М=0) амплитуды боковых составляющих равны нулю и спектр АМ-сигнала переходит в спектр несущего колебания. При М≤1 амплитуда изменяется в пределах от минимальной до максимальной . Исключая постоянное напряжение , получим формулу, удобную для экспериментального определения коэффициента модуляции:

(10.23)

Рис.10.5

Если же М>1, то возникают искажения, называемые перемодуляцией. Наличие таких искажений в АМ-сигнале может привести к потере передаваемой информации.

На практике однотональные АМ-сигналы используются либо для учебных целей, либо для исследовательских целей. Реальный же модулирующий сигнал имеет сложный спектральный состав. Математически такой сигнал, состоящий из N гармоник, можно представить тригонометрическим рядом

(10.24)

В этом соотношении амплитуды гармоник сложного модулирующего сигнала E_i произвольны, а их частоты образуют упорядоченный спектр Ω₁< Ω₂<Ω_i<… Ω_N.

Подставляя (10.24) в (10.18), после несложных преобразований получим выражение АМ-сигнала с начальной фазой несущего φ₀=0:

(10.25)

где М_i=kE_i/U_н – совокупность парциальных(частичных) коэффициентов модуляции.

Эти коэффициенты характеризуют влияние отдельных гармонических составляющих сложного модулирующего сигнала на общее изменение амплитуды полученного высокочастотного модулированного колебания.

Воспользовавшись тригонометрической формулой произведения двух косинусов и проделав несложные выкладки, запишем выражение (10.25) в следующем виде:

(10.26)

Из соотношения (10.26) видно, что в спектре сложного АМ-сигнала, наряду с несущим колебанием содержатся группы верхних и нижних боковых составляющих, являющихся масштабными копиями модулирующего сигнала и расположенных симметрично относительно несущей частоты ω₀. Отсюда следует вывод: ширина спектра сложного АМ-сигнала равна удвоенному значению наивысшей частоты в спектре модулирующего сигнала Ω_N.

В качестве примера на рис.10.6 показаны спектральные диаграммы трехтонального (состоящего из трех разных гармоник) модулирующего сигнала S_e(ω) и соответствующего ему АМ-сигнала S_АМ(ω).

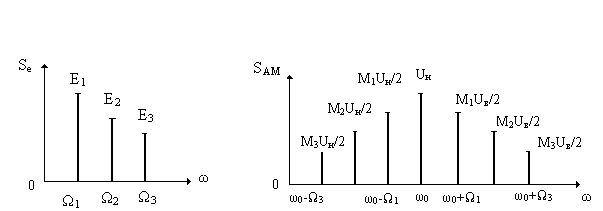
а) б)

Рис. 10.6