Вопросы для экспресс – контроля.

1. Запишите нестационарное уравнение Шредингера и сформулируйте условия, которым должна удовлетворять волновая функция.

2. В каком случае возможен переход от нестационарного уравнения Шредингера к стационарному?

3. Как определяется вероятность обнаружения действия микрочастицы в заданный момент времени в данной точке пространства?

4. Что такое собственные значения энергии и собственные волновые функции?

5. Как определяются собственные значения энергии и собственные волновые функции микрочастицы, находящейся в одномерной бесконечно глубокой потенциальной яме?

6. В чем суть туннельного эффекта и почему он невозможен в рамках классической механики?

7. Запишите выражение, определяющие энергетический спектр, одномерного квантового осциллятора. Почему его минимальная энергия не равна нулю?

1. *Напишите уравнение Шредингера для свободного электрона, движущегося в положительном направлении оси ox со скоростью . Найдите решение этого уравнения.

2. *Докажите, что если волновая функция циклически зависит от времени, т.е. , то плотность вероятности есть функция только координат частицы.

3. *Какого размера должен быть потенциальный ящик для того, чтобы локализованный в нем электрон имел на самом глубоком уровне энергию 0,1эВ; 1 эВ;10 эВ и 1 МэВ?

4. *Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме ширины с абсолютно непроницаемыми стенками ( ). Найти вероятность пребывания частица в областях:

   1. ;

   2. ;

   3. .

5. Вычислить энергию, которая необходима, чтобы перевести частицу, заключенную в потенциальном ящике, с третьего уровня на четвертый. Задачу решить:

   1. для электрона при ширине ящика 0,1 нм и 1 мм;

   2. для частицы с массой 10^-6 г при ширине ящика 1 мм.

6. Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы такова, что энергетические уровни расположены весьма густо. Найти плотность уровней 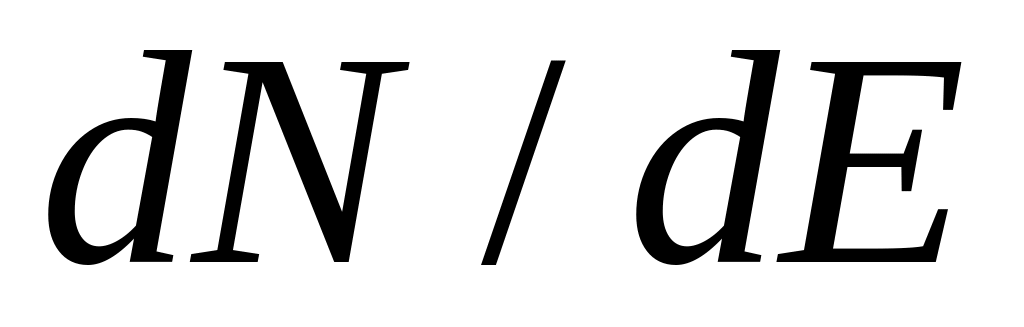, т.е. их число на единичный интервал энергии, в зависимости от 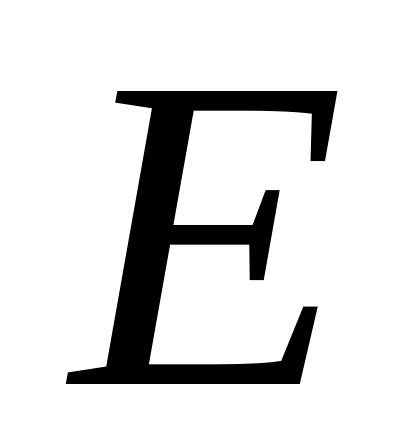. Вычислить для эВ, если см.

7. Частица массы находится в одномерном потенциальном поле , вид которого показан на рисунке, где .

Найти:

1. уравнение, определяющее возможные значения энергии частицы в области ; привести это уравнение к виду , где . Показать с помощью графического решения, что возможное значение энергии образуют дискретный спектр;

2. минимальное значение величины , при котором появляется первый энергетический уровень в области . При каком минимальном значении появляется n-ый уровень?

3. определите вероятность нахождения частицы с энергией в области , если

1. *Частица подходит слева к потенциальному барьеру, изображенному на рисунке.

Частица может пройти сквозь барьер и отразится от него. Какой вид будут иметь уравнение Шредингера и волновые функции в I-ой, II-ой и III-ей областях, если полная энергия частицы ? Получите выражение для коэффициента прозрачности и рассчитайте его для электрона при высоте барьера эВ и ширине нм, если энергия электрона составляет:

1. ;

2. .

1. Волновая функция в основном состоянии атома водорода имеет вид 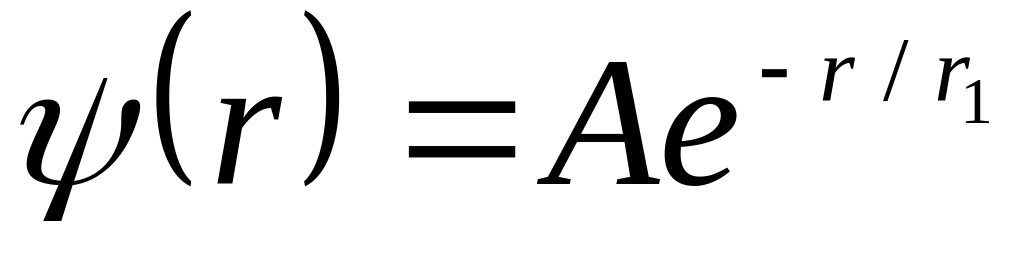, где – некоторая постоянная, 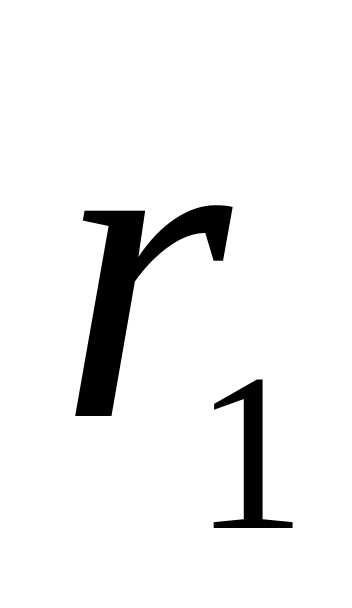– первый Боровский радиус. Найти:

   1. наиболее вероятное расстояние между электроном и ядром;

   2. среднее значение кулоновской силы, действующей на электрон;

   3. средне значение потенциальной энергии электрона в поле ядра.

СТРОЕНИЕ АТОМОВ. РЕНТГЕНОСКОЕ ИЗЛУЧЕНИЕ.

Цель – закрепить представление о распределении электронов по энергетическим уровням в атоме, принципе Паули, периодической системе элементов.

Указания к организации самостоятельной работы.

Изучите теоретический материал по конспекту лекций и учебным пособиям [3, стр. 136-140; 2, стр. 455-466]. Обратите внимание на то, что для описания поведения микрочастицы в сферически симметричном силовом поле необходимо решить уравнение Шредингера, записав его в сферических координатах:

, где – волновая функция, – полная энергия частицы, – ее потенциальная энергия.

В атоме водорода (или водородоподобном ионе) потенциальная энергия имеет вид:

, где – зарядовое число, – элементарный заряд, – диэлектрическая постоянная

Из решения уравнения Шредингера можно получить собственные значения энергии электрона в атоме

, где – главное квантовое число.

Соответствующие собственные волновые функции будут определяться значением трех квантовых чисел , , – главного, орбитального и магнитного.

Если – определяет собственные значения энергии, то определяет орбитальный момент импульса, а – магнитный момент электрона.

Если учесть, что электрон в атоме обладает спином (спиновый момент импульса) и соответствующим ему магнитным моментом, то для однозначного задания состояния электрона в атоме необходимо задать значения спинового квантового числа , которое может принимать значения .

Таким образом, состояние электрона в атоме характеризуется заданием четырех квантовых чисел: , , , . Согласно принципу Паули, в атоме не может находиться два (и более) электронов, характеризующихся одинаковым набором четырех квантовых чисел.