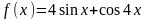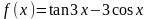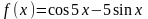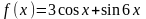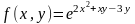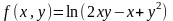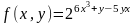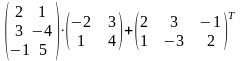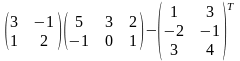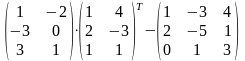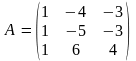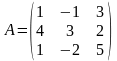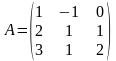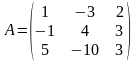- •Задания для домашних контрольных работ1
- •1(II). Найти f(X)
- •2 (III). Найти частные производные первого порядка функции .
- •3 (IV). Найти дифференциал первого порядка функции в указанной точке a.
- •5 (VIII). Вычислить
- •6 (XI). Для заданной матрицы а найти обратную матрицу двумя способами (методом Гаусса и с помощью алгебраических дополнений), убедиться в совпадении результатов. Провести проверку.
- •7 (IX). Решить системы уравнений методом Гаусса и Крамера, сравнить ответы.
- •8 (XII). Найти наибольшее и наименьшее значения функции на заданно отрезке.
- •9 (XV). Построить область, описанную системой ограничений (неравенств). Решить графически задачу линейного программирования.
- •10 (XVI). Решить задачи, используя классическое определение вероятности и (или) теоремы сложения и умножения.
- •11 (XVII). Решить задачи, используя формулу Бернулли.
- •12 (XVIII). Для случайной величины X, заданной табличным законом распределения, найти математическое ожидание и дисперсию.
Задания для домашних контрольных работ1
1(II). Найти f(X)
1)
|
6)
|
11)
|
2)
|
7)
|
12)
|
3)
|
8)
|
13)
|
4)
|
9)
|
14)
|
5)
|
10)
|
15)
|
2 (III). Найти частные производные первого порядка функции .
1)
|
6)
|
11)
|
2)
|
7)
|
12)
|
3)
|
8)
|
13)
|
4)
|
9)
|
14)
|
5)
|
10)
|
15)
|
3 (IV). Найти дифференциал первого порядка функции в указанной точке a.
-
1)
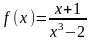 ,
a=2
,
a=29)
 ,
a=0
,
a=02)
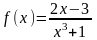 ,
a=2
,
a=210)
 ,
a1
,
a13)
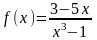 ,
a=0
,
a=011)
 ,
a=0
,
a=04)
 ,
a=1
,
a=112)
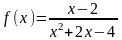 ,
a=1
,
a=15)
 ,
a=1
,
a=113)
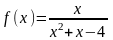 ,
a=3
,
a=36)
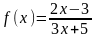 ,
a2
,
a214)
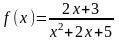 ,
a0
,
a07)
 ,
a0
,
a015)
 ,
a2
,
a28)
 ,
a1
,
a1
4 (VI). Для прямой на плоскости, заданной общим уравнением, выписать вектор нормали и значение углового коэффициента. Составить уравнение прямой, параллельной данной и проходящей через точку А. Найти угловой коэффициент прямых, перпендикулярных данной, и составить уравнение прямой, перпендикулярной данной и проходящей через точку В. Записать уравнение прямой (АВ). Построить графики этих четырех прямых.
1)
 ,
A(1;-2),
B(3;7)
,
A(1;-2),
B(3;7)
2)
 ,
A(-1;2),
B(3;5)
,
A(-1;2),
B(3;5)
3)
 ,
A(-2;1),
B(3;3)
,
A(-2;1),
B(3;3)
4)
 ,
A(1;1), B(-3;4)
,
A(1;1), B(-3;4)
5)
 ,
A(1;-1), B(2;5)
,
A(1;-1), B(2;5)
6)
 ,
A(1;-3), B(2;1)
,
A(1;-3), B(2;1)
7)
 ,
A(-2;2), B(3;1)
,
A(-2;2), B(3;1)
8)
 ,
A(-1;2), B(3;6)
,
A(-1;2), B(3;6)
9)
 ,
A(1;-2), B(3;7)
,
A(1;-2), B(3;7)
10)
 ,
A(1;2), B(-3;-2)
,
A(1;2), B(-3;-2)
11)
 ,
A(1;3), B(-2;5)
,
A(1;3), B(-2;5)
12)
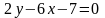 ,
A(3;-1), B(1;2)
,
A(3;-1), B(1;2)
13)
 ,
A(3;-3), B(1;5)
,
A(3;-3), B(1;5)
14)
 ,
A(1;1), B(3;-4)
,
A(1;1), B(3;-4)
15)
 ,
A(3;-2), B(1;4)
,
A(3;-2), B(1;4)
5 (VIII). Вычислить
1)
|
2)
|
3)
|
4) |
5)
|
6)
|
7)
|
8)
|
9)
|
10)
|
11) |
12) |
13) |
14)
|
15) |
|
6 (XI). Для заданной матрицы а найти обратную матрицу двумя способами (методом Гаусса и с помощью алгебраических дополнений), убедиться в совпадении результатов. Провести проверку.
1)
|
6)
|
11)
|
2)
|
7)
|
12)
|
3)
|
8)
|
13)
|
4)
|
9)
|
14)
|
5)
|
10) |
15)
|