III. Полигон и гистограмма.

Пример 6. Построить полигон частот по данному распределению выборки:

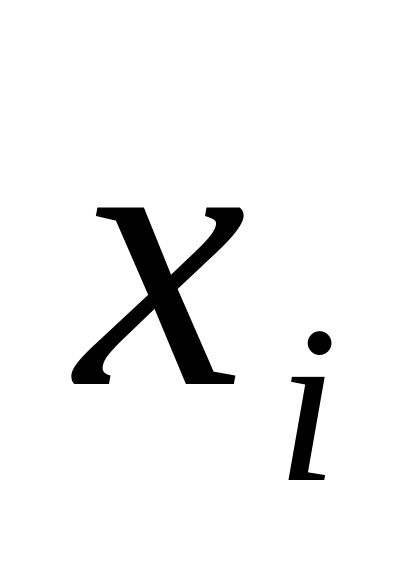
	2	3	5	6
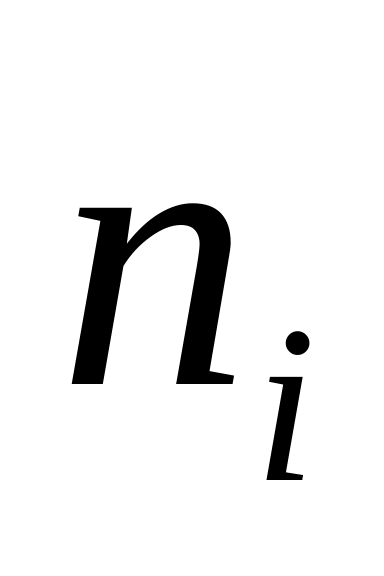
	10	15	5	20

Решение. Отложим на оси ОХ значения , а на оси ординат – соответствующие им частоты . Соединив полученные точки отрезками прямых, получим искомый полигон частот (рис.3).

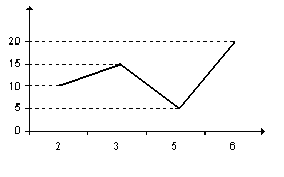
Рисунок 3

Пример 7. Построить гистограмму частот распределения по данной выборке:

Значение	-2	0	1	2	3	5	7
Частота	4	5	7	8	6	2	1

.

Промежуток	[-2;0,25]	[0,25;2,5]	[2,5;4,75]	[4,75;7]
	9	15	6	3
	4

По оси ОХ отложим частичные интервалы - вычисленные промежутки, а по оси ОУ значения , по которым строим прямоугольники. Совокупность прямоугольников является искомой гистограммой с площадью, равной объему выборки (рис.3).

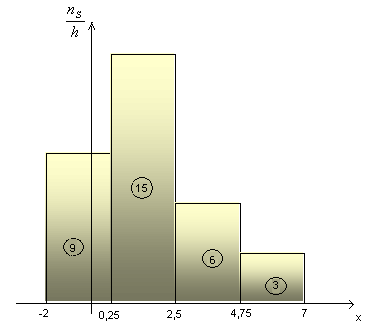
Рисунок 4

IV. Точечные оценки.

Пример 1. Контрольные обмеры диаметров болтов дали следующие результаты: 2,31; 2,28; 2,29; 2,28; 2,32; 2,28; 2,32; 2,29; 2,31; 2,32.

Найти точечные оценки для диаметра болта и его дисперсии в контролируемом процессе производства.

.

Пример2.

Известно, что случайная величина имеет распределение Пуассона

,

неизвестным является параметр . Используя указанные выше методы получения точечных оценок, найти по выборке значение неизвестного параметра .

Решение.

Решим задачу двумя методами.

1 Метод моментов

В формуле подсчитаем и , используя заданную выборку:

.

.

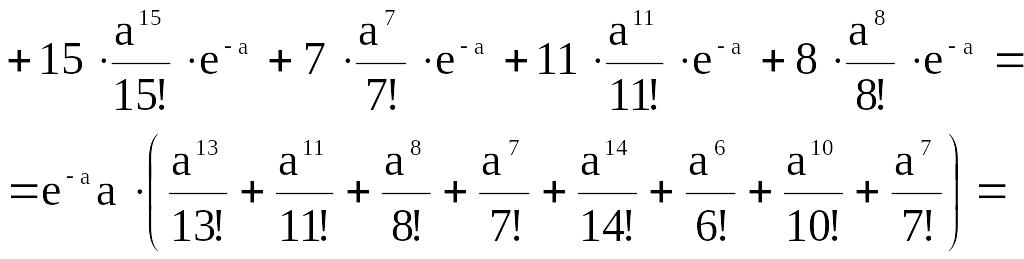
Из равенства получаем , т.е. .

2 Метод максимального подобия

Составим функцию правдоподобия:

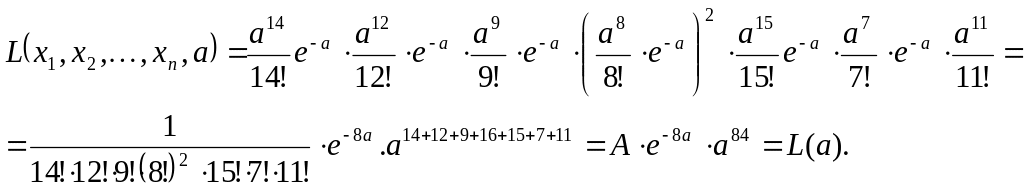
Исследуем функцию одной переменой на экстремум.

Необходимым условием экстремума является =0 или

.

, . Следовательно, - критическая точка.

Достаточным условием экстремума является знак второй производной в критической точке:

.

.

Следовательно, значение является максимальным значением функции , отсюда понятно название метода максимального правдоподобия.

Ответ: .

Пример 3.

Известно, что случайная величина имеет биноминальное распределение

,

неизвестным является параметр . Используя методы получения точечных оценок, найти по реализации выборки значение неизвестного параметра .

Решение.

Пусть выборка будет, что и в предыдущей задаче. Решим поставленную задачу двумя способами.

1 Метод моментов

В формуле вычислим правую и левую части, используя условие задачи: выборка .

.

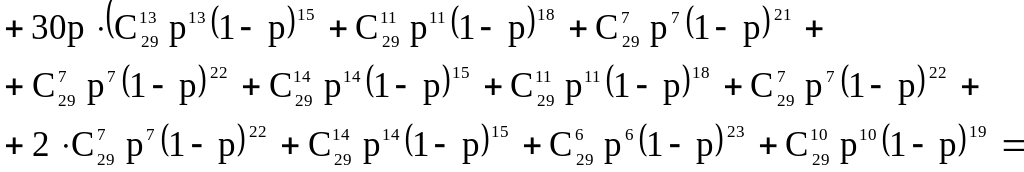
Подставляя в формулу , получим , .