3.Закон больших чисел.

В случае большого числа экспериментов можно получить гораздо более содержательные результаты. В узком смысле под «законом больших чисел» понимается ряд теорем, в основе которых лежит тот факт, что хотя отдельное наблюдение случайной величины может иметь довольно широкий разброс, средние значения ее ведут себя намного устойчивее. В широком смысле этот закон утверждает, что при очень большом числе случайных явлений средний результат перестает быть случайным и может быть предсказан с большой степени определенности. Некоторые результаты в этом направлении дает использование неравенства Чебышева.

Неравенство Чебышева. Для любого имеет место неравенство

Законов больших чисел много. Один из них - знаменитый закон в форме Чебышева дается следующей теоремой.

Теорема 1. Пусть случайные величины

попарно независимы и существует число С такое, что для всех i выполнены неравенства . Тогда для любого имеем:

Теорема 2. (Бернулли). Пусть - число успехов в независимых испытаниях, - вероятность успеха в каждом испытании. Тогда при любом : ,

отсюда вытекает, что

Геометрически эта вероятность равна площади криволинейной трапеции.

Задача 1. Используя неравенство Чебышева, оценить вероятность того, что случайная величина отклониться от своего математического ожидания менее чем на , где дисперсия, N - номер варианта.

Р е ш е н и е : N=31, пусть

События противоположные,

следовательно тогда

в силу неравенства Чебышева, тогда

Задача 2. Случайная величина с одинаковой вероятностью может принимать одно из двух значений: i² или -i².Выяснить, удовлетворяет ли последовательность попарно независимых случайных величин закону больших чисел:

.

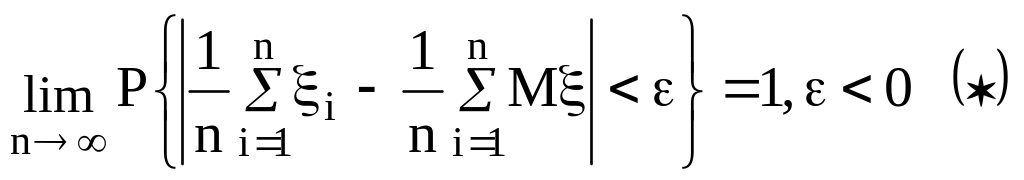Решить задачу для

Решение: . По условию тогда

следовательно, в формуле остается ряд

Ряд сходиться, т. к. известный ряд сходиться при

и расходиться при .

Ряд расходиться, т. к. при

В силу этого в первом случае при

а во втором случае при это условие не выполнимо.

Ответ: при закон больших чисел выполняется, при - не выполняется.

Задача 3. На отрезке случайно выбраны n чисел, точнее, рассматриваются n независимых случайных величин равномерно распределенных на отрезке . Найти вероятность того, что их сумма заключена между х₁ и х₂ , т. е.

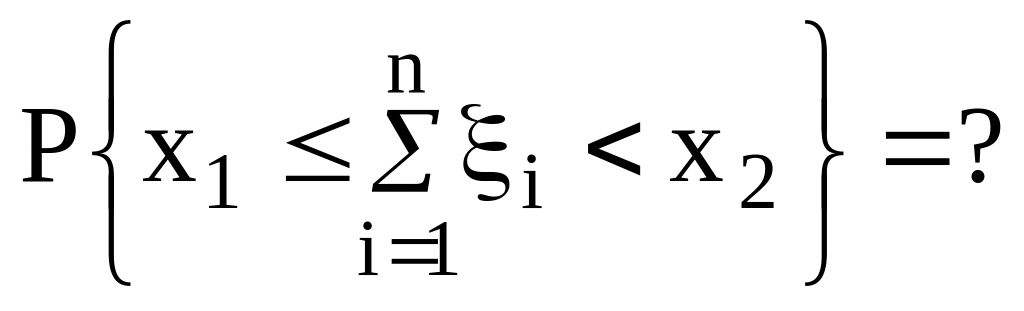
Решение:

Известно

т. к. то по условию имеем

тогда

Ответ:

Аудиторные задания

1. Построить график и , если

2. Автобусы идут с интервалом 5 минут. Считая, что случайная величина - время ожидания автобуса на остановке – распределена равномерно на указанном интервале, найти среднее время ожидания и дисперсию времени ожидания.

3. Время безотказной работы радиоаппаратуры является случайной величиной , распределенной по показательному закону с параметром . Вычислить математическое ожидание и дисперсию.

4. Дана плотность распределения случайной величины Х: если

х[b-;(b+] и p(x)=0 вне этого интервала. Найти параметр , функцию распределения случайной величины Х и вероятность выполнения неравенства .

5. Дано Найти значение С и функцию распределения Х.

6. Дано: P(|X-M(X)|< ε)>=0,9 и D(X)=0,009.

Используя неравенство Чебышева, найти ε.

Отв. ε=0,3.