25. Графический метод решения матричных игр типа 2 n
и типа m 2.
Самаров- ТЕОРИЯ ИГР.pdf СТР 15-18
МатМетоды в экономике. Лекция 10 (стр. 5-конец)
МатМетоды в экономике. Лекция 11 – продолжение
26. Сетевой график производства работ. Критическое время завершения процесса работ. Некритические операции
Самаров- ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ..pdf СТР 15-21
27. Кратчайший путь из источника в сток в сети.
Самаров- ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ..pdf СТР 22
28. Предоставление ссуд на срок в 1 год на основе годовых процентных и учетных ставок.
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 11
29. Предоставление ссуд на срок, выражаемый в годах, по схемам простых и сложных процентов на основе процентной ставки.
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 15
30. Уравнение регрессии и его построение
Регрессия бывает парная и множественная. Уравнение регрессии отражает – тренд развития. Уравнения регрессии может быть – линейное, гиперболическое, синусоидальное и т.д. Будем рассматривать линейною регрессию.
Парная – есть у и х1. Наиболее распространенный метод МНК. Т.е. надо построить невязку S(A,B) = (yi-a-bxi)2 -> min . Минимум получается, если производная уравнения по каждому коэффициенту = 0.
Более подробно см. в ТЕТРАДНЫХ лекциях по эконом.-мат. Моделированию.
Множественная – зависимая у, объясняющие -
.
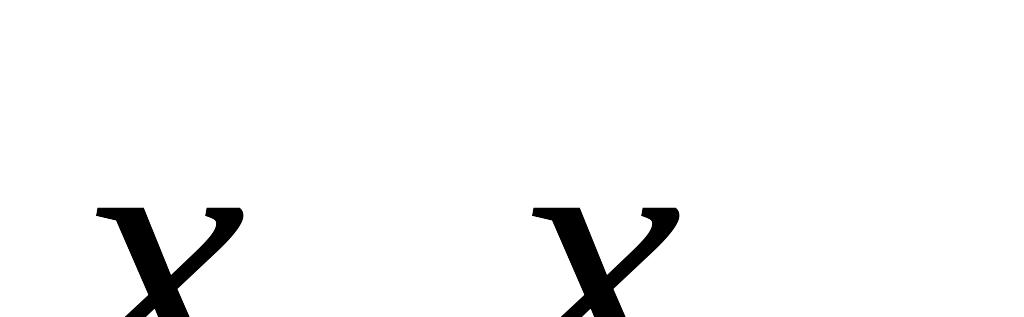где y - теоретические значения результативного признака, полученные по уравнению регрессии, b0, b1,…, bk - коэффициенты (параметры) уравнения регрессии, - объясняющие переменные.
Коэффициент парной линейной регрессии bi имеет смысл показателя силы связи между вариацией факторного признака х и вариацией результативного признака у. Знак bi указывает направление этого изменения.
В таком случае результаты наблюдений должны быть представлены уравнениями, полученными в каждом из n опытов:
(1)
или в виде матрицы результатов наблюдений:
где n – количество опытов, k - количество факторов.
Для решения системы уравнений (1) необходимо, чтобы количество опытов было не меньше k + 1, т.е. n ≥ k + 1.
Заданием
множественного регрессионного анализа
является построение такого уравнения
прямой k-мерном
пространстве, отклонение результатов
наблюдений
от которого были бы минимальными.
Используя для этого метод наименьших
квадратов, получаем систему нормальных
уравнений:
Данную систему уравнений представим в матричной форме:
(ХТХ)В = XTY (2)
где В - вектор-столбец коэффициентов уравнения регрессии;
X - матрица значений факторов;
Y - вектор-столбец функции отзыва;
XТ - транспонированная матрица X.
При
,
,
они соответственно равны:
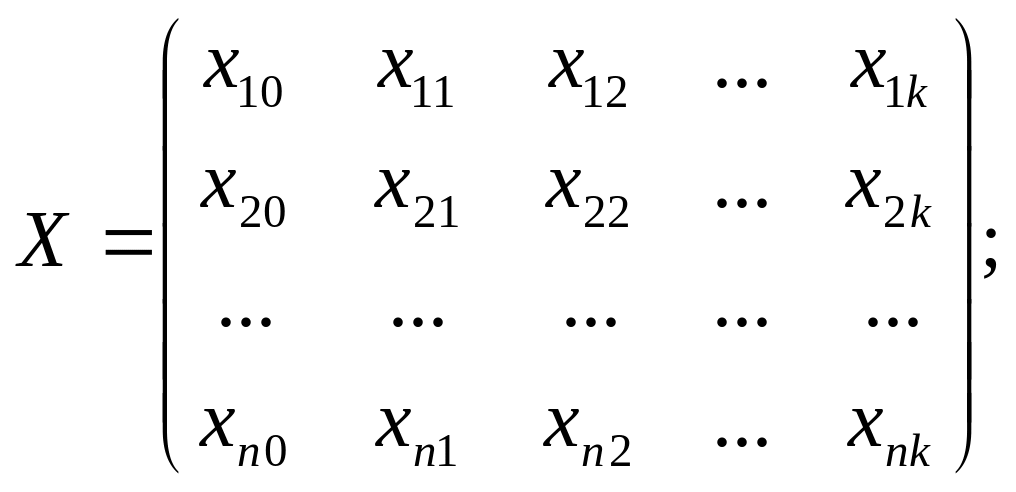
Перемножив правую и левую часть уравнения (2) на обратную матрицу (ХТХ)-1, получим:
Каждый коэффициент уравнения регрессии вычисляется по формуле:
где
- элементы обратной матрицы (ХТХ)-1.
31. Способы определения срока возврата ссуды в годах для ссуд, выданных на срок, исчисляемый в днях (английский, французский и немецкий способы).
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 28
32. Наращение по схемам простых и сложных процентов в случае плавающих процентных ставок.
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 22
33. Сравнение денежных сумм, выплаченных в различные моменты времени.
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 32
34. Конечные и бесконечные финансовые ренты.
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 68
35. Современная величина ренты.
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 71
36. Потребительский кредит.
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 47
37. Ломбардный кредит.
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 30
38. Операция учета векселей.
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 73