2.2.3 Классификация параметров иос

Внутренними параметрами системы, однозначно определяющими ее состояние, будут размеры отверстий в сетках r₁ и r₂ , расстояние между сетками d , размер сечения пучков в плоскости обработки R_П , расстояние между пучками R , расстояние до обрабатываемой поверхности L и размер ИОС R_C , определяющий размер пучка ИИ, а также технологические параметры: ток элементарных пучков J (или плотность j ), ускоряющее напряжение U, температура электронов Т_е и распределение ионов в плазме n(R), являющееся обобщенным параметром конструкции и работы разрядной камеры ИИ. Необходимо также учесть тип используемого рабочего газа, например его массовое число M и массу иона M_i . Независимой переменной будет координата R, направленная по радиусу моделируемой системы, а фазовой переменной - угол расходимости пучка .

Внешними параметрами может выступать давление в области обработки Р или электромагнитные поля Е, Н. В качестве входных параметров могут выступать начальное значение отверстая в экранной сетке r_1Н , начальный шаг размещения отверстий R_Н и размер системы R_C, а выходными параметрами для групп ячеек будут r_1i , r_2i , di и R_ОПТ, соответствующие максимальной плотности ионного тока и его равномерности на поверхности обработки при сохранении необходимой жесткости сеток, которая может быть задана минимальной величиной перемычки между соседними отверстиями . За входной параметр для ИОС можно принять и функцию распределения ионов в плазме разрядной камеры ИИ n(R).

2.2.4 Математическая модель иос

При получении модели будем считать, что процесс травления осуществляется при низком давлении и при отсутствии внешних полей, поэтому можно не учитывать их влияние на формируемый пучок ионов. Сделаем также предположение, что необходимая равномерность обработки пластины обеспечивается без взаимного перекрытия пучков на ее поверхности, т.е. R=2R_П, а распределение плотности тока ионов по сечению каждого из пучков равномерное. При выводе формул воспользуемся геометрическими моделями рис. 2.2 и 2.3.

При заданной функции распределения ионов в плазме ИИ плотность тока вычисляется по формуле

, (2.1)

где j(R) - плотность тока в заданной точке, мА/см²; e – заряд, Кл; k – постоянная Больцмана; T_e - температура электронов, К; m – масса иона, кг; М - массовое число рабочего газа.

Полный ток пучка определяется как произведение его плотности на площадь отверстия в первой сетке:

, (2.2)

а плотность тока на обрабатываемой поверхности будет равна

. (2.3)

Угол расходимости пучка определяется по формуле

. (2.4)

Для ячейки, представленной на рис. 2.2, максимальное значение ионного тока обеспечивается при следующем соотношении параметров:

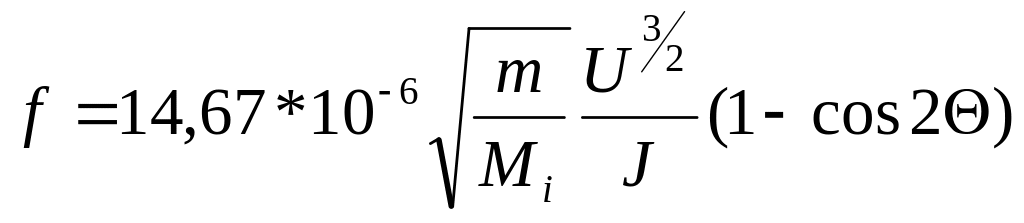, (2.5)

где f - значение табулированной функции, зависящее от отношения радиусов кривизна сферического конденсатора C=R₁/R₂ (см. табл. 2.1); m - масса электрона, кг; Mi - масса иона, кг; U - ускоряющее напряжение, В.

Из формулы (2.5) определяется значение f, затем из табл. 3.1 находится соответствующее ему число С , по которому рассчитываются значения R₁ и R₂ :

(2.6)

Таблица 2.1. - Значения табулированной функции отношения R₁/R₂.

C	f	C	f	C	F
1	0	2,35	1,274	5,4	9,318
1,025	0,0007	2,4	1,358	5,5	9,664
1,05	0,0024	2,45	1,444	5,6	10,014
1,075	0,0054	2,5	1,531	5,7	10,368
1,1	0,0095	2,55	1,62	5,8	10,727
1,125	0,0148	2,6	1,712	5,9	11,091
1,15	0,0213	2,65	1,805	6	11,46
1,175	0,0287	2,7	1,902	6,2	12,207
1,2	0,0372	2,75	1,999	6,4	12,969
1,225	0,0466	2,8	2,098	6,6	13,747
1,25	0,0571	2,85	2,199	6,8	14,54
1,275	0,0685	2,9	2,302	7	15,35
1,3	0,0809	2,95	2,406	7,2	16,175
1,325	0,0942	3	2,512	7,4	17,015
1,35	0,1084	3,05	2,62	7,6	17,87
1,375	0,1237	3,1	2,73	7,8	18,738
1,4	0,1398	3,15	2,841	8	19,62
1,425	0,1565	3,2	2,954	8,2	20,518
1,45	0,174	3,25	3,069	8,4	21,43
1,475	0,1925	3,3	3,185	8,6	22,357
1,5	0,2118	3,35	3,302	8,8	23,298
1,525	0,2318	3,4	3,421	9	24,25
1,55	0,2526	3,45	3,542	9,2	25,215
1,575	0,2743	3,5	3,664	9,4	26,192
1,6	0,2968	3,55	3,788	9,6	27,181
1,625	0,32	3,6	3,913	9,8	28,18
1,65	0,344	3,65	4,04	10	29,19
1,675	0,3687	3,7	4,168	11	34,44
1,7	0,394	3,75	4,298	12	39,98
1,725	0,42	3,8	4,429	13	45,79
1,75	0,4467	3,85	4,561	14	51,86
1,775	0,474	3,9	4,695	15	58,19
1,8	0,502	3,95	4,831	16	64,74
1,825	0,531	4	4,968	17	71,54
1,85	0,5605	4,1	5,246	18	78,56
1,875	0,5905	4,2	5,529	19	85,81
1,9	0,6215	4,3	5,814	20	93,31
1,925	0,653	4,4	6,108	25	133,5
1,95	0,6848	4,5	6,407	30	178,2
1,975	0,7171	4,6	6,712	35	227,1
2	0,75	4,7	7,022	40	279,6
2,05	0,818	4,8	7,336	50	394
2,1	0,888	4,9	7,653	60	520
2,15	0,961	5	7,976	70	656
2,2	1,036	5,1	8,304	80	801
2,25	1,113	5,2	8,638	90	954
2,3	1,192	5,3	8,976	100	1114

После этого определяется размер отверстия во второй сетке и расстояние между сетками:

(2.7)

Таким образом, рассчитана центральная ячейка ИОС. Для расчета параметров следующей группы соседних ячеек делается шаг R и по формуле (2.1) определяется j(R) для новой точки. Радиус нового отверстия в первой сетке из условий постоянства тока каждого пучка определяется по формуле

, (2.8)

Подставляя это значение в формулу (2.4) вместо r₁, определим угол расходимости пучка в новой ячейке, а затем по формулам (2.5)-(2.7) – все остальные параметры данной ячейки. Так последовательно идет расчет параметров ИОС до значения R=R_c.

В качестве ограничения вводится минимальный размер перемычки между отверстиями, при котором еще сохраняется механическая прочность сеток. С этой целью после каждого очередного шага R идет проверка по формуле

. (2.9)

При невыполнении этого условия корректируется шаг или начальное значение размера отверстия в первой сетке, В результате проведения нескольких циклов расчета при различных R и их анализе выбирается минимальное значение R , при котором однако сохраняется механическая прочность сеток, т.е. на всей их поверхности выполняется условие (2.9).

Представленная математическая модель учитывает взаимосвязи между основными параметрами ИОС и параметрами плазмы ИИ, что позволяет на ее основе разработать методику для проектирования двухсеточных ИОС, обеспечивающих максимальную плотность и равномерность ионных пучков большого диаметра.