
- •2.1 Теоретические сведения 28
- •Лабораторная работа № 1 Моделирование внутрикамерного устройства для процесса нанесения пленок с кольцеобразным источником материала
- •1.1 Теоретические сведения
- •1.1.1 Общие сведения о моделируемом объекте
- •1.1.2. Постановка задачи
- •1.1.3. Построение геометрической модели
- •1.1.4. Математическая модель процесса осаждения пленки
- •1.2 Лабораторное задание
- •1.2.1 Техническое оснащение
- •1.3 Методика выполнения работы
- •1.3.1 Требования к отчету
- •1.3.2 Инструкция по работе с программой «magna»
- •1.3.3 Контрольные вопросы
- •Лабораторная работа № 2 Моделирование системы ионного травления с ионным источником и ионно-оптической системой
- •2.1 Теоретические сведения
- •2.1.1 Общие сведения
- •2.1.2 Постановка задачи
- •2.2 Моделирование системы травления
- •2.2.1 Конструктивная схема системы обработки
- •2.2.2 Геометрическая модель иос
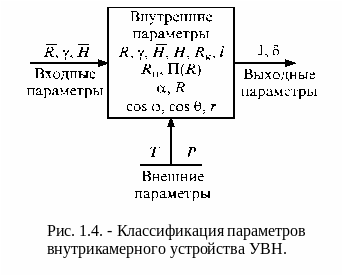
- •2.2.3 Классификация параметров иос
- •2.2.4 Математическая модель иос
- •2.3 Лабораторное задание
- •2.3.1 Техническое оснащение
- •2.4 Методика выполнения работы
- •2.4.1 Требования к отчету
- •2.4.2 Инструкция по работе с программой «ios»
- •2.4.3 Контрольные вопросы
- •Список литературы
1.1.4. Математическая модель процесса осаждения пленки
При создании модели прежде всего необходимо выделить те параметры, которые оказывают наиболее существенное влияние на моделируемый процесс, и сделать ряд допущений, позволяющих получить удобную и допустимо простую, но адекватную модель.
В
общем случае толщина пленки на участке
конденсации будет зависеть от скорости
распыления с участка dS
в направлении радиуса-вектора
![]() ,
расстояния между участками r,
углов
и ,
эмиссионной характеристики, рассеяния
атомов при столкновении с молекулами
рабочего газа, коэффициента конденсации
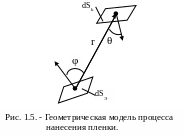
и ряда других параметров. Геометрическая
модель процесса нанесения пленки
показана на рис. 1.5.
,
расстояния между участками r,
углов
и ,
эмиссионной характеристики, рассеяния
атомов при столкновении с молекулами
рабочего газа, коэффициента конденсации
и ряда других параметров. Геометрическая
модель процесса нанесения пленки
показана на рис. 1.5.
При моделировании в первом приближении можно сделать следующие допущения:
- распределение эмитируемых с распыляемой поверхности атомов в пространстве подчиняется косинусному закону;
- распыленные частицы летят по прямолинейным траекториям и рассеиваются за счет столкновений незначительно;
- частица конденсируется в точке соударения с поверхностью (не учитывается миграция по поверхности и отражение от нее).
Тогда для косинусного закона имеем следующее выражение для расчета толщины осажденной пленки:
h =
v![]()
![]() dt, (1.1)
dt, (1.1)
где v - коэффициент, пропорциональный скорости распыления; Т0 - время осаждения.
Для стационарного случая
h = v (cos×cos/r2)T0.
Для поверхностного источника при определении толщины пленки нужно провести интегрирование по поверхности распыления, при этом необходимо учесть, что поверхность распыляется неоднородно в направлении радиуса мишени. Для этого вводится закон распределения плотности ионного тока по радиусу мишени, который в связи со сложностью моделирования плазмы и магнитной системы должен быть определен эмпирически или задан. Следует отметить, что в общем случае закон распределения распыленных атомов в пространстве может отличаться от косинусного. Тогда также необходимо учесть это отклонение введением соответствующего члена.
В результате учета вышеуказанных факторов выражение для расчета толщины пленки примет вид
h =
v
![]()
![]() dSЭ
dt, (1.2)
dSЭ
dt, (1.2)
где Ф(cos ) - функция, описывающая реальное (некосинусное) распределение распыленных атомов в пространстве; П(R) - полином, учитывающий распределение плотности ионного тока по радиусу зоны распыления; SЭ - площадь распыляемой поверхности (поверхности эмиссии).
Таким образом, для решения поставленной задачи необходимо выявить:
- распределение эмитированных атомов в пространстве Ф(cos );
- распределение плотности ионного тока по радиусу зоны распыления П(R);
- аналитические выражения для cos , cos и r.
Реальное распределение эмитированных атомов в пространстве может быть выражено в виде
Ф(cos ) = (1 + m)cosm , (1.3)
где m - эмпирический коэффициент, учитывающий отклонение эмиссионной характеристики от косинусного закона распределения.
Распределение плотности ионного тока по радиусу мишени, зависящее от условий локализации плазмы и конфигурации зоны распыления, может быть описано полиномами различного вида, например:
П(R) =![]() iRi или П(R) =
i|
iRi или П(R) =
i|![]() –R|i.
–R|i.
В случае равномерного распределения ионного потока по зоне распыления П(R) = 1. При треугольном профиле распределения (в центре зоны максимум, на границах - ноль) получим
П(R) = 1 – (2/l)| –R|. (1.4)
При интегрировании по распыляемой поверхности в качестве переменных удобно выбрать радиус мишени R и полярный угол . Тогда элементарный участок поверхности dS определится из выражения
dSЭ = (R dR d)/cos . (1.5)
Подставив (1.5) в (1.2), получим выражение для интенсивности потока частиц в заданную точку конденсации (скорость осаждения v0) для стационарной внутрикамерной системы:
v0
=
dh/dt
=
v![]()
![]() dRd
. (1.6)
dRd
. (1.6)
Используя геометрическую модель рис. 1.3, находим:
 (1.7)
(1.7)
где H1 = +( – R)tg ; G 2 = Rк2 – 2RкRcos + R2.
Подставив (1.7) в (1.6), получим аналитическую модель моделируемой системы для косинусного распределения в виде:
v0 = v
![]() dR
d, (1.8)
dR
d, (1.8)
где R1=![]() – 0,5
l
cos
;
R2=
+
0,5
l
cos
.
– 0,5
l
cos
;
R2=
+
0,5
l
cos
.
Для обеспечения
адекватности модели необходимо ввести
ограничения, учитывающие тот факт, что
процесс осаждения пленки между участками
распыления и конденсации реализуется
в том случае, если угол между
радиусом-вектором
и нормалями к соответствующим участкам
![]() и
и
![]() не
превышает 90.
Данные ограничения могут быть записаны
в виде cos > 0,
cos > 0.
При невыполнении этих условий
подынтегральное выражение обращается
в ноль.
не
превышает 90.
Данные ограничения могут быть записаны
в виде cos > 0,
cos > 0.
При невыполнении этих условий
подынтегральное выражение обращается
в ноль.
Для оценки равномерности пленки по толщине в осесимметричной системе достаточно определить распределение пленки по радиусу пластины. С этой целью находятся значения v0 для N точек на радиусе пластины с некоторым шагом Rк. Неравномерность пленки можно оценить по формуле
= [(v0max – v0min)/( v0max + v0min)]100 %, (1.9)
где
v0max =![]() {v0(n)};
v0min =
{v0(n)};
v0min =![]() {v0(n)}.
{v0(n)}.
Коэффициент перед интегралом в выражении (1.8) представляет собой скорость эмиссии распыленных частиц. Он зависит от типа источника (точечный или поверхностный) и скорости распыления vр, которая в свою очередь зависит от энергии и массы ионов, вида распыляемого материала, плотности ионного тока и ряда других параметров. Для поверхностного источника коэффициент можно рассчитать по формуле:
= vp/
=
![]() , (1.10)
, (1.10)
где vp - скорость распыления, м/с; ji - плотность ионного тока, А/м2; е – элементарный заряд, Кл; z - кратность заряда иона; Кр - коэффициент распыления, атом/ион; А - атомная масса распыляемого материала, кг/моль; NA - число Авогадро, атом/моль; - плотность распыляемого материала, кг/м3.
Недостатком полученной модели (1.8) является то, что она не учитывает влияния рабочего давления на процесс осаждения и достаточно адекватна только для низких давлений, при которых рассеяние потока распыленных атомов на атомах рабочего газа за счет столкновений незначительно. Кроме того, модель не учитывает изменения условий осаждения во времени в процессе эрозии мишени, когда из-за неравномерной плотности ионного потока распыляемая поверхность приобретает неплоскую форму.
Влияние рабочего давления можно учесть через коэффициент распыления, вводя в него поправки на явления обратного рассеяния (отражения) и обратной диффузии распыленных атомов. Обратное рассеяние представляет собой процесс возврата распыленного атома на мишень при его столкновении с атомом рабочего газа. Этот процесс происходит на расстояниях, не превышающих длины свободного пробега распыленной частицы, и зависит от соотношения масс и кинетических энергий соударяющихся частиц. Под обратной диффузией следует понимать возвращение на мишень распыленных атомов с расстояний, значительно превышающих длину свободного пробега, которые за счет многочисленных столкновений с атомами газа уменьшили свою энергию до значений, соответствующих средней кинетической энергии атомов рабочего газа.
Для случая, когда масса распыленного атома больше массы атома газа, основным процессом возвращения распыленных атомов на мишень является обратная диффузия, и величина коэффициента распыления с учетом этого явления может быть определена по формуле
К = Кр [2,3а0 / (2,3а0 + P0 r – La)], (1.11)
где а0 - длина свободного пробега распыленных атомов при единичном давлении и температуре 273 К; P0 = 273 P/Т - давление газа, приведенное к температуре 273 К; P – реальное давление рабочего газа; r - расстояние между участками распыления и конденсации; La - средняя длина направленного пробега распыленного атома при единичном давлении газа. Возврат распыленных атомов возможен с расстояний, для которых р0 r > La. Для меньших расстояний все распыленные атомы достигают поверхности конденсации, т.е. К = Кр.
Когда масса распыленных атомов меньше массы атомов газа, то для области P0 r La наблюдается обратное рассеяние, и в этом случае
К = 0,5Кр[1 + exp(–Р0 r/аT)]. (1.12)
Для области P0 r > La будет наблюдаться возврат распыленных атомов за счет как обратного рассеяния, так и обратной диффузии, в связи с чем
К = 0,5Кр {2,3а0[1 + exp(–P0 r/аT)]/(2,3а0 + P0 r)}, (1.13)
где аT - средняя длина свободного пробега атома при единичном давлении и заданной температуре газа.
Величина La рассчитывается по формуле
La = аT N,
где N - среднее число столкновений атомов распыленного вещества с частицами газа, после которого энергия распыленных атомов Еа уменьшается до уровня тепловой энергии атомов газа Ег,
N = lg(Eг/Еа)/lg(1 - Emax/Ea),
где Emax - максимальная доля энергии, передаваемая распыленным атомом атому газа при столкновении.
В табл. 1.1 приведены значения некоторых величин для ряда распыляемых в аргоне материалов, рассчитанных по формулам молекулярной кинетики газов. Для аргона mа = 6,6210–26 кг, ra = 1,9210–10 м.
Таблица 1.1. - Параметры распыленных в аргоне атомов различных материалов.
Параметр |
Al |
Si |
Ti |
Cu |
Nb |
Mo |
Ag |
Ta |
W |
Au |
ma10–25, кг |
0,447 |
0,462 |
0,799 |
1,052 |
1,570 |
1,596 |
1,795 |
3,007 |
3,176 |
3,271 |
ra10–10, м |
1,43 |
1,34 |
1,46 |
1,28 |
1,45 |
1,39 |
1,44 |
1,46 |
1,40 |
1,44 |
a010–3, Пам |
9,25 |
9,70 |
7,92 |
8,24 |
6,44 |
6,63 |
6,18 |
5,02 |
5,10 |
4,90 |
aТ10–3, Пам |
14,24 |
14,95 |
12,12 |
12,70 |
9,92 |
10,22 |
9,52 |
7,74 |
7,84 |
7,54 |
a10–2, Пам |
2,22 |
2,21 |
1,40 |
2,18 |
3,24 |
3,50 |
2,96 |
5,60 |
5,80 |
5,52 |
Влияние эрозии зоны распыления на равномерность пленки в первом приближении можно учесть, считая, что профиль зоны распыления меняется согласно закону распределения плотности ионного тока П(R). Наиболее простая модель получается при треугольном профиле распределения ионного тока (см. формулу (1.4)). В этом случае распыляемую поверхность можно представить как суперпозицию двух конических поверхностей. Геометрическая модель процесса нанесения пленки с учетом эрозии мишени показана на рис. 1.6.
Первая
коническая поверхность располагается
на отрезке [R1,![]() ]
и задана параметрами
]
и задана параметрами
![]() ,
,
![]() ,
1,
l1,
а вторая – на отрезке [
,R2]
и имеет
параметры
,
1,
l1,
а вторая – на отрезке [
,R2]
и имеет
параметры
![]() ,
,
![]() ,2,
l2.
Максимальная глубина эрозии hэ
определяется скоростью распыления vp
(см. формулу
(1.10)) и длительностью процесса.
,2,
l2.
Максимальная глубина эрозии hэ
определяется скоростью распыления vp
(см. формулу
(1.10)) и длительностью процесса.

Параметры выделенных распыляемых поверхностей выражаются через параметры мишени:
1 = – arctg(2hэ/l);
2 = 2 – 1;
l1 =
l2 =![]() ;
;
Rэ =![]() - 0,5 l cos
+ lэ
сos
1;
- 0,5 l cos
+ lэ
сos
1;
![]() =
=![]() +
0,5 l
sin
– 0,5 lэ
sin 1;
+
0,5 l
sin
– 0,5 lэ
sin 1;
= + 0,5 l sin – lэ(sin 1+ 0,5sin 2);
=![]() –
0,5 lэ
cos 1;
–
0,5 lэ
cos 1;
= + 0,5 lэ cos 2.
Для проектировщика внутрикамерного устройства важным параметром является коэффициент полезного использования материала мишени, представляющий собой отношение количества осажденного на пластину материала к количеству распыленного с мишени материала. Количество осажденного материала (объем V0) можно определить как произведение среднего значения толщины пленки на площадь пластины:
V0 = vpT0Rп2, (1.14)
где vp - значение скорости осаждения (среднеарифметическое) для N точек на радиусе пластины, расположенных с шагом Rк, по которым проводится оценка равномерности пленки, а Т0 - длительность процесса осаждения пленки.
Аналогично количество распыленного материала Vp можно оценить как произведение среднего значения толщины распыленного слоя на площадь зоны распыления:
Vp = ([ vpП(Ri) ]/N)([R22 – R12]T0 / cos ). (1.15)
Разработанная
математическая модель процесса осаждения
пленки связывает основные конструктивные
и технологические параметры внутрикамерного
устройства и учитывает наиболее важные
факторы, влияющие на процесс формирования
пленки, что позволяет создавать на ее
базе пакет прикладных программ для
расчета и оптимизации внутрикамерных
устройств УВН с кольцеобразными
источниками распыляемого материала.
Модель реализована в виде программы
“MAGNA”, которая позволяет проводить
оптимизацию конструкции внутрикамерного
устройства по трем параметрам (![]() и
)
четырьмя различными методами (“золотого
сечения” - для варианта оптимизации по
одному параметру, покоординатного
спуска, симплекс-методом и методом
Монте-Карло - для многопараметрической
оптимизации – по двум и более параметрам).
и
)
четырьмя различными методами (“золотого
сечения” - для варианта оптимизации по
одному параметру, покоординатного
спуска, симплекс-методом и методом
Монте-Карло - для многопараметрической
оптимизации – по двум и более параметрам).
В настоящее время созданы более сложные модели, учитывающие произвольное положение подложки относительно мишени. Модели позволяют выбирать форму зоны распыления, при которой обеспечивается заданная равномерность пленки при высоком коэффициенте использования материала мишени.
