1.1.3. Построение геометрической модели

Наиболее важными геометрическими параметрами внутрикамерного устройства УВН являются параметры, характеризующие форму и размеры распыляемой поверхности, поверхности конденсации, а также относительное положение этих поверхностей в процессе осаждения пленки.

Кольцеобразную форму распыляемой поверхности (рис. 1.2) в общем случае можно представить конической (или в виде суперпозиции конических участков), определяемой следующими геометрическими параметрами: средним радиусом , углом конусности  и шириной зоны распыления l (или внутренним R₁ и внешним R₂ радиусами). При  = 0 имеет место планарная распыляемая мишень, при положительном значении угла - коническая мишень с внутренней распыляемой поверхностью, а при отрицательном - с внешней конической распыляемой поверхностью. При R₁ = 0 имеем дисковую мишень.

Геометрическая модель внутрикамерного устройства показана на рис. 1.3. Взаимное положение пластины и мишени можно определить расстоянием от поверхности подложки до плоскости, проходящей через середину зоны распыления, определяемую средним радиусом .

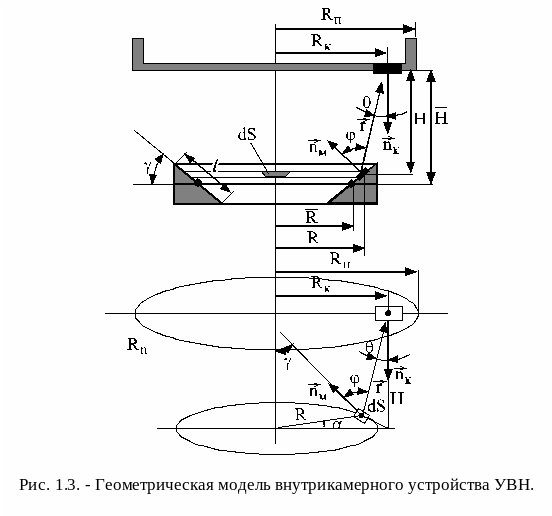
Размер планарной поверхности конденсации или положение участка конденсации на пластине радиусом R_п определяется радиусом R_к. Поверхность распыления можно представить как суперпозицию элементарных участков dS, определяемых через приращение полярного угла  и текущего радиуса R. Процесс конденсации будет также зависеть от расстояния между участками распыления и конденсации, определяемого радиусом-вектором , углом распыления , представляющим собой угол между нормалью к распыляемой поверхности мишени и радиусом-вектором , а также углом конденсации  между нормалью к поверхности конденсации и тем же радиусом-вектором.

Используя построенную геометрическую модель внутрикамерного устройства и аналитическую модель, описывающую процесс распыления, переноса и конденсации вещества, можно через геометрические зависимости записать в аналитическом виде взаимосвязь между геометрическими и технологическими параметрами осесимметричного внутрикамерного устройства УВН с кольцеобразным источником материала.

Для построения модели необходимо провести классификацию параметров, описывающих объект проектирования или влияющих на его функционирование. Внутренними параметрами являются: параметры мишени ,  и l, параметры поверхности конденсации R_к, R_п, параметр плазмы П(R), учитывающий изменение характеристик плазмы по радиусе распыляемой поверхности, параметры взаимного положения участков мишени и пластины и Н, переменные интегрирования (независимые переменные)  и R, фазовые переменные cos  (или Ф(cos )), cos  и r. Эти параметры представляют собой набор зависимых переменных и постоянных величин.

Внешними параметрами являются температура Т, давление Р. В качестве входных параметров могут выступать параметры оптимизации (зависимые переменные) ,  и , а в качестве выходных - толщина пленки h (или скорость осаждения v₀) и ее равномерность по толщине =Δh. В общем случае набор входных и выходных параметров может меняться в зависимости от постановки задачи оптимизации. Пример классификации параметров для задачи оптимизации геометрических параметров внутрикамерного устройства по критерию равномерности осаждения пленки и толщине показана на рис. 1.4.