Задача №5

Задание. С помощью интерполяционной формулы Ньютона найти значение первой и второй производных при значении аргумента для функции, заданной таблично.

0.8 1.2 1.6 2.0 2.4 2.8 3.2 3.6	2.857 3.946 4.938 5.801 6.503 7.010 7.288 7.301

Решение. Пусть функция , задана в равноотстоящих точках отрезка значениями . Для нахождения на производных , и т.д. функцию приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов , т.е.

Имеем

где .

Перепишем ее, выполнив умножение:

Так как

то

Аналогично, так как

то

.

Таким же способом в случае надобности можно вычислить и производные функции любого порядка.

Иногда требуется находить производные функции в основных табличных точках . В этом случае формулы численного дифференцирования упрощаются. Так как каждое табличное значение можно считать за начальное, то положив будем иметь:

и

.

Положим ; тогда . Воспользуемся для вычисления формулами

,

получающимися из первой интерполяционной формулы Ньютона.

Находим

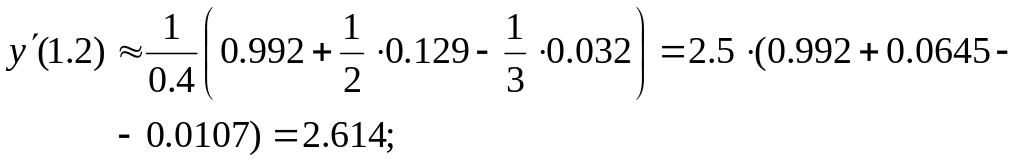
Задача №6

Задание. 1) Вычислить интеграл по формуле трапеций с тремя десятичными знаками.

2) Вычислить интеграл по формуле Симпсона при ; оценить погрешность результата, составив таблицу конечных разностей.

1) ; 2) .

Решение. Точное значение определенного интеграла вычисляется по формуле Ньютона-Лейбница через первообразную :

.

Если же первообразная неизвестна или функция задана таблицей или графиком, то применяются методы приближенного интегрирования. Формулы для приближенного интегрирования получаются при замене площади криволинейной трапеции на сумму площадей простых геометрических фигур, площадь которых легко вычисляется.

Разделим интервал на равных частей длиной . При этом . Обозначим через значение функции в точках .

Метод трапеций. Если площадь каждой полоски, на которые разбита криволинейная трапеция точками , считать приближенно равной площади соответствующей трапеции, то для вычисления интеграла получаем формулу трапеций (рис. 3)

Рис. 3

Метод Симпсона. Метод Симпсона применим при разбиении интервала на четное число частей . Каждая пара полосок ограничивается сверху параболой, проходящей через три точки. Затем вычисляется площадь каждой пары полосок, ограниченной сверху параболой. Сумма площадей всех пар полосок является приближенным значением определенного интеграла (рис. 4).

Рис. 4

1) Для достижения заданной степени точности необходимо определить значение так, чтобы

(*)

Здесь ; ; , где .

Находим , ;

.

Положим , тогда неравенство (*) примет вид , откуда , т.е. ; возьмем .

Вычисление интеграла проводим по формуле

,

где ; ; .

Все вычисления приведены в таблице 3:

Таблица 3

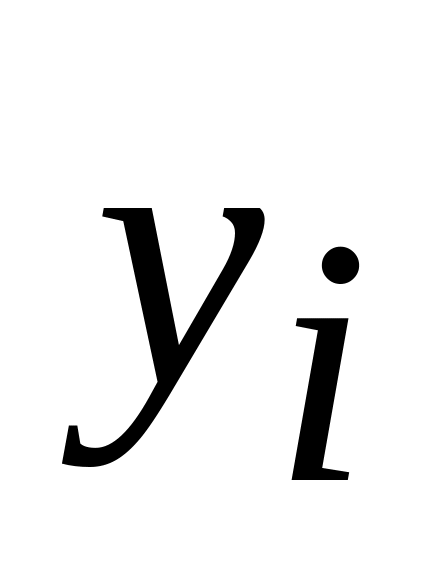
0 1 2 3 4 5 6 7 8 9 10 11	0.7 0.73 0.76 0.79 0.82 0.85 0.88 0.91 0.94 0.97 1.00 1.03	0.88386 0.85572 0.82898 0.80366 0.77973 0.75700 0.73546 0.71501 0.69551 0.67700 0.65937 0.64259

Продолжение табл. 3

12 13 14 15 16 17 18 19 20

1.06 1.09 1.12 1.15 1.18 1.21 1.24 1.27 1.30

0.62657 0.61140 0.59669 0.58272 0.56935 0.55658 0.54431 0.53253 0.52129

Таким образом,

.

2) Согласно условию , поэтому .

Расчетная формула имеет вид

где , .

Вычисления значения функции запишем в таблице 4:

Таблица 4

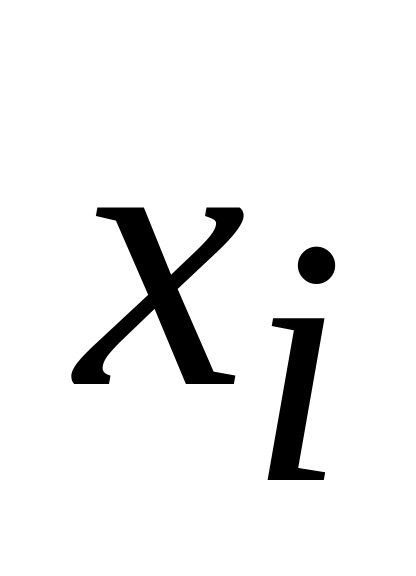
0 1 2 3 4	1.2 1.25 1.30 1.35 1.40	0.1211 0.1520 0.1782 0.2000 0.2176

Продолжение табл. 4

5 6 7 8

1.45 1.50 1.55 1.60

0.2312 0.2410 0.2473 0.2503

Следовательно,

.