Задача №2

Задание. Дана таблица значений функции . Используя метод наименьших квадратов, подобрать для заданных значений и

1) линейную функцию ;

2) квадратичную функцию .

X	0.5	1.0	1.5	2.0	2.5	3.0
Y	0.31	0.82	1.29	1.85	2.51	3.02

Решение. Пусть  для неизвестной функции в точках экспериментальным путем получены значения . Интерполяция позволяет аппроксимировать таблично заданную функцию с помощью более простой функции . При этом требуется выполнение в узлах интерполяции равенства ( ). В ряде случаев выполнение этого условия затруднительно или даже нецелесообразно. При большом числе узлов интерполяции степень интерполирующего многочлена получается высокой. Поэтому точность такой аппроксимации гарантирована лишь в небольшом интервале порядка несколько шагов сетки. Для другого интервала приходится заново вычислять коэффициенты интерполяционной формулы. В практических приложениях желательно иметь единую приближенную формулу ( ), пригодную для большего отрезка . При этом точность приближения может оцениваться по разному. В основу обычно берется рассмотренное отклонение

( ).

В связи с этим возникает задача приближения таблично заданной функции многочленом , который имеет не слишком высокую степень и дает в некотором смысле разумную точность аппроксимации.

Для решения этой задачи воспользуемся методом наименьших квадратов. В методе наименьших квадратов за меру отклонения многочлена от функции принимается их среднее квадратичное отклонение

.

Задача состоит в том, чтобы в аппроксимирующем многочлене подобрать коэффициенты так, чтобы минимизировать Так как коэффициенты выступают в роли независимых переменных функции , то необходимым условием минимума является равенство нулю всех частных производных , , …, . Приравнивая к нулю эти частные производные получим систему уравнений

После преобразования система принимает вид

Определитель этой системы отличен от нуля, поэтому эта система имеет единственное решение .

1) Аппроксимируем таблично заданную функцию линейной .

Составим систему для определения

Предварительно вычисляем , , , Следовательно,

Решая эту систему, находим и : , .

Искомый многочлен .

2) Аппроксимируем таблично заданную функцию квадратичной функцией .

Составим систему для определения

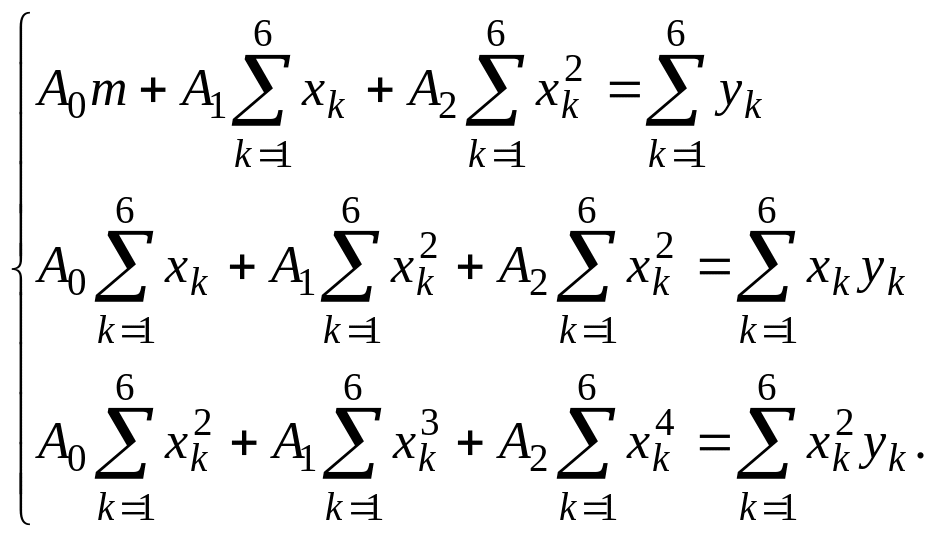
Предварительно вычисляем

,

,

,

,

, ,

Получим систему уравнений вида

Решая эту систему, находим , и : , , .

Искомый многочлен

Задача №3

Задание. Получить приближенное решение системы методом простой итерации с точностью 0.01.

Решение. Пусть дана система линейных уравнений

(1)

Введя в рассмотрение матрицы

, , .

систему (1) можно записать в виде матричного уравнения

. (2)

Предполагая, что диагональные коэффициенты , разрешим первое уравнение системы (1) относительно , второе – относительно и т.д. Тогда получим эквивалентную систему

(3)

где , при

и при

Введя матрицы

, ,

систему (3) можем записать в матричной форме

. (4)

Для решения системы (4) применим метод последовательных приближений. За начальное приближение принимаем, например, столбец свободных членов .

Далее, последовательно строим матрицы-столбцы

, ,…. , , …

Если последовательность приближений имеет предел

,

то этот предел является решением системы (4) и, cледовательно, решением равносильной системы (1).

Для того чтобы процесс итераций сходился к единственному решению этой системы, независимо от выбора начального приближения, необходимо выполнение для приведенной системы (3) по меньшей мере одного из условий (достаточное условие сходимости метода итераций)

или

.

Приведем заданную систему уравнений к виду (3)

В качестве начального приближения возьмем систему чисел ; ; .

После первого шага получим:

После второго:

Дальнейшие вычисления располагаем в таблице 1:

Таблица 1

0 1 2 3 4 5 6	1.2000 1.2000 0.9640 1.0098 0.9975 1.0007 0.9998	0.0000 1.0600 0.9440 1.0104 0.9966 1.0009 0.9997	0.0000 1.1600 0.9480 1.0144 0.9960 1.0012 0.9997

Точное решение ( ) практически достигается на 6-ой итерации.