Министерство образования и науки Российской Федерации ФГБОУ ВПО Ивановский государственный химико-технологический университет

Факультет химической техники и кибернетики

Кафедра технической кибернетики и автоматики

Домашняя работа

по дисциплине:

«Автоматизация технологических процессов и производств»

Выполнила:

студентка группы 4/36

Черникова М.М.

Проверил:

проф. Лабутин А.Н.

Иваново, 2013

1. Емкостной смеситель

1.1. Концептуальная модель

Рис. 1.1. Принципиальная схема аппарата

В химический реактор емкостного типа с механической мешалкой подается исходный реагент потоком с расходом . Второй входной поток с расходом служит для разбавления смеси до необходимой концентрации.

Назначение аппарата: осуществление сложной многостадийной реакции.

Цель функционирования:

а) получение реакционной смеси с заданным значением концентрации целевого вещества.

б) получение реакционной смеси с заданной температурой.

Показателем эффективности управления является:

а) ,

где - заданное значение концентрации на выходе, - текущее значение концентрации.

б) ,

где t - заданное значение концентрации на выходе, - текущее значение концентрации.

Классификация переменных

Переменные состояния объекта:

• объём реактора - V;

• концентрация на выходе - C;

• температура в реакторе - t.

Входные переменные объекта:

• расходы на входе и выходе из аппарата потока - υ₁, υ₂;

• концентрация вещества во входном потоке – С₁;

• температуры входных потоков t₁, t₂.

1.2. Математическая модель

Допущения:

1) структура потоков в обеих фазах описывается моделью идеального перемешивания;

2) теплофизические свойства всех потоков и реакционной смеси постоянны;

3) потерями тепла и тепловой емкостью стенок пренебрегаем;

4) уровень газожидкостной смеси в аппарате постоянен. (можно не писать)

Уравнения модели динамики.

Уравнение общего материального баланса (есть, если V )

- масса в аппарате.

Уравнение материального баланса по компонентам:

- количество вещества.

Уравнение теплового баланса для емкости:

- масса в аппарате

- удельная теплоемкость вещества (сколько Дж может содержать 1 кг вещества)

- количество теплоты

Уравнения модели динамики:

Начальные условия:

.

Если указано, что модель необходимо разработать при свободном истечении, значит расход на выходе зависит от величины уровня жидкости в аппарате.

где - коэффициент расхода, - площадь свободного сечения отверстия (клапана), h - уровень

1.3. Линеаризация модели в виде передаточных функций.

Канал .

Используем уравнение общего материального баланса и уравнение материального баланса по компонентам:

Заменяем на :

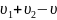Для получения передаточной функции по исследуемым каналам необходимо перейти от абсолютных величин в уравнении модели к их отклонениям от значений в статике. Для этого даем приращение входной - регулирующей и регулируемой. Остальные переменные считаем равные в статике.

Запишем уравнения динамики в отклонениях от статики:

Из полученного уравнения вычитаем уравнение статики.

Начальные условия:

.

Уравнение делим на коэффициент при -

- апериодическое звено первого порядка

где .

Преобразуем по Лапласу:

2. Емкостной теплообменник с подачей пара в рубашку

2.1. Концептуальная модель

Рис. 2.1. Принципиальная схема аппарата

В теплообменник объемом V подается поток жидкости с расходом и температурой . На вход рубашки поступает пар, на выходе – конденсат.

Назначение аппарата: проведение теплопередачи.

Цель функционирования: получение выходного потока с заданной температурой.

Показателем эффективности управления является:

,

где t - заданное значение концентрации на выходе, - текущее значение концентрации.