
Лабораторная работа №1
.doc
Задача 1.2.
Дано уравнение
![]() .
Предполагается, что один из коэффициентов
уравнения (в индивидуальном варианте
помечен *) получен в результате округления
по дополнению. Исследовать зависимость
абсолютной погрешности корня от
абсолютной погрешности коэффициента
уравнения.
.
Предполагается, что один из коэффициентов
уравнения (в индивидуальном варианте
помечен *) получен в результате округления
по дополнению. Исследовать зависимость
абсолютной погрешности корня от
абсолютной погрешности коэффициента
уравнения.
1.2.11.
![]() .
.
Теория:
Утверждение. Формулы для границ погрешностей функции одной переменной имеют вид:
![]() ,
(1)
,
(1)
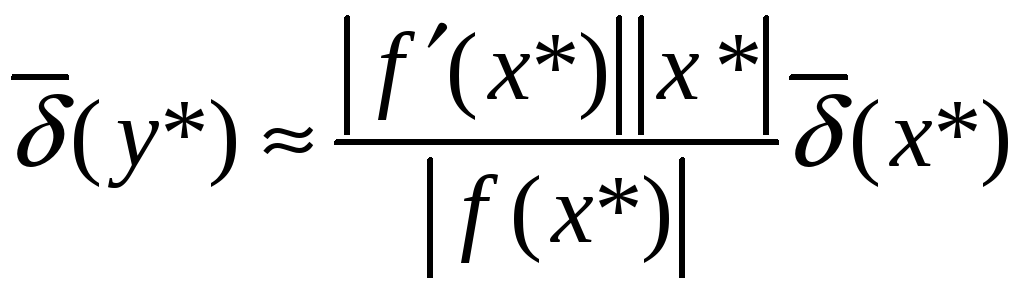 ,
(2)
,
(2)
Будем называть задачу хорошо обусловленной, если малым погрешностям входных данных соответствуют малые погрешности результата. И плохо обусловленной в противном случае.
![]()
![]()
абсолютное число
обусловленности
относительное число
обусловленности
![]()
![]()
Если
![]()
![]()
ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:
1.Найти корень уравнения.
2.Произвести теоретическую оценку абсолютной погрешности корня в зависимости от погрешности коэффициента.
3.Вычислить корень уравнения при нескольких различных значениях коэффициента в пределах заданной точности.
4.Сравнить полученные результаты (см. ПРИЛОЖЕНИЕ 1.C).
5. Найти число обусловленности задачи.
![]()
![]()
![]()
![]()
![]()
- корень уравнения
![]() -коэффициент,
полученный в результате округления по
дополнению
-коэффициент,
полученный в результате округления по
дополнению
Вычислим корень нескольких различных значениях коэффициента в пределах заданной точности:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- теоретическая оценка абсолютной погрешности корня
- получили хорошее соответствие с теоретической оценкой.
Найдём относительное число обусловленности задачи:
![]()
![]()
![]()
-относительное число
обусловленности задачи, меньше 10,
следовательно, задачу можно считать
хорошо обусловленной.
![]()
![]()
![]()
Вывод: выполнив
вычислительный эксперимент, взяв другие
значения коэффициента
![]() в пределах погрешности, получили, что
практически полученные погрешности
хорошо соответствуют с теоретически
полученной погрешностью. Также определено,
что данная задача является хорошо
обусловленной.
в пределах погрешности, получили, что
практически полученные погрешности
хорошо соответствуют с теоретически
полученной погрешностью. Также определено,
что данная задача является хорошо
обусловленной.
