
- •11 Ряди
- •11.1 Числові ряди
- •11.1.1 Числові знакододатні ряди ,
- •Алгоритм дослідження збіжності числових знакододатних рядів.
- •11.1.2 Числові знакозмінні , , як додатні так і від’ємні, та знакопочережних , ряди
- •Алгоритм дослідження збіжності числових знакопочережних рядів :
- •4. Запишіть відповідь.
- •11.2 Степеневі ряди
- •Алгоритм визначення області збіжності степеневих рядів.
- •3. Запишіть відповідь.
- •3. Запишіть відповідь.
- •5. Запишіть відповідь.
- •5. Запишіть відповідь.
- •5. Запишіть відповідь.
- •11.3 Розкладання функцій в ряди Тейлора і Маклорена
- •Алгоритм розкладання функцій в ряд Маклорена.
- •11.4 Ряди Фур’є Алгоритм розкладання функцій в ряд Фур’є
- •4. Запишіть відповідь.
- •4. Запишіть відповідь.
- •4. Запишіть відповідь.
4. Запишіть відповідь.
Підставляючи
отримані значення
![]() ,
,
![]() ,
,
![]() в формулу (11.14) отримуємо шуканий розклад
заданої функції в ряд Фур’є:
в формулу (11.14) отримуємо шуканий розклад
заданої функції в ряд Фур’є:
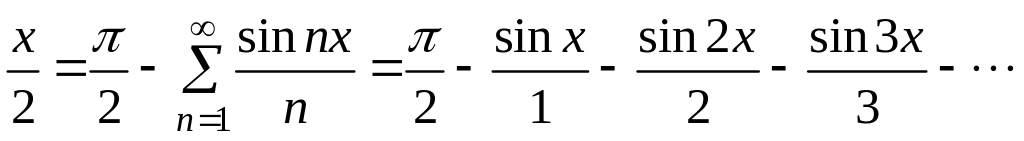
Цей
розклад справедливий, тобто отриманий
ряд збігається до заданої функції у
всіх точках її області визначення
![]() .
У граничних точках
і
.
У граничних точках
і
![]() сума ряду дорівнює
сума ряду дорівнює
![]() (у цих точках усі члени ряду, крім першого,
обертаються в нуль).
(у цих точках усі члени ряду, крім першого,
обертаються в нуль).
Приклад
11.18. Розкласти в ряд Фур’є функцію
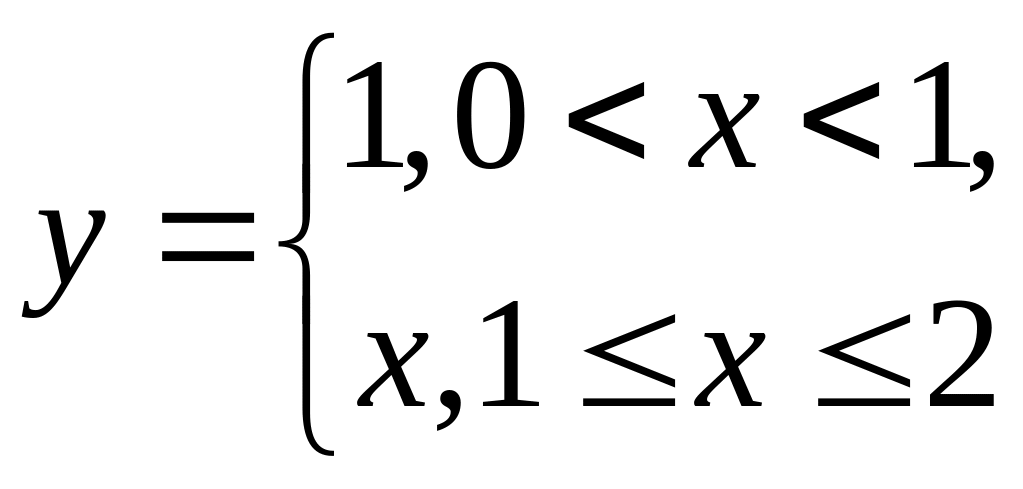
1. Зробіть графік даної функції.
Наведемо графік функції, одержаної періодичним продовженням її на всю числову вісь.
(графік)
Проаналізуйте функцію і оберіть потрібні формули для подальшого розв’язування прикладу.
Дана функція є функцією загального виду.
Будемо
застосовувати формули (11.14), в яких
покладемо
.
Інтервал інтегрування
![]() точкою
розіб’ємо на дві частини, оскільки у
кожній з них функція задана різними
формулами.
точкою
розіб’ємо на дві частини, оскільки у
кожній з них функція задана різними
формулами.
3. Знайдіть коефіцієнти ряду Фур’є.
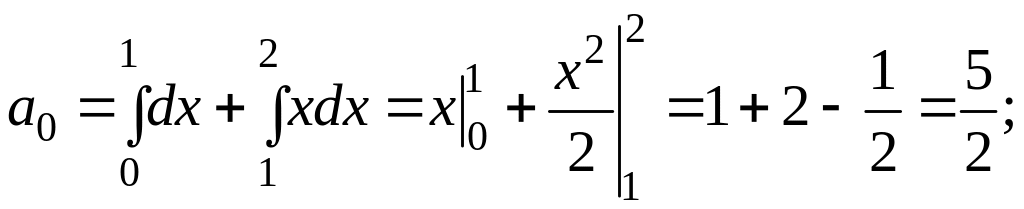
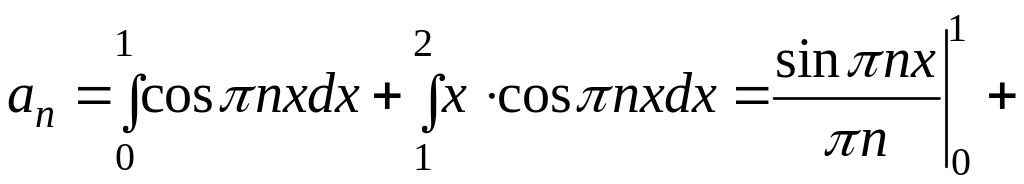
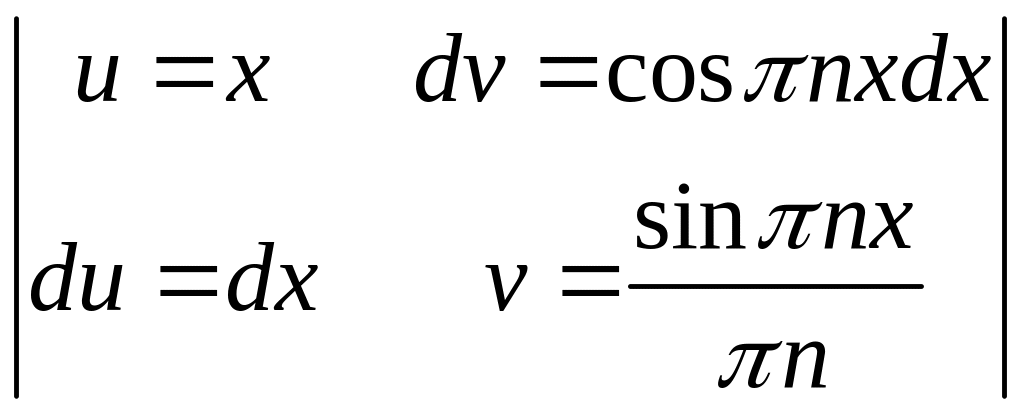
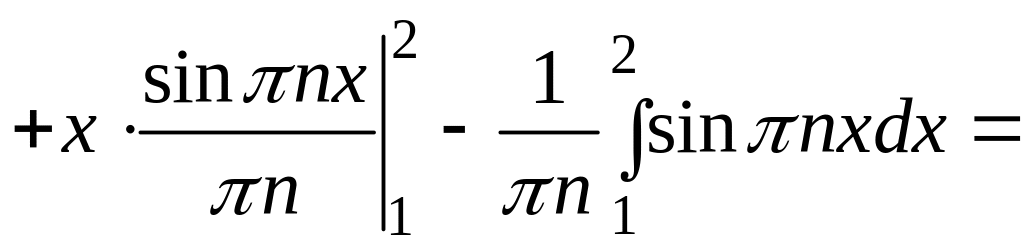
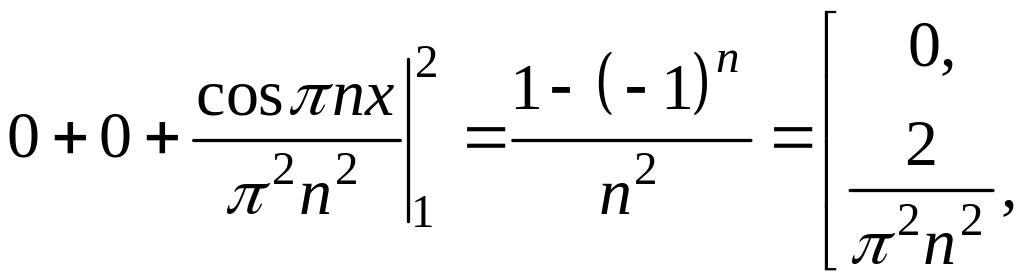
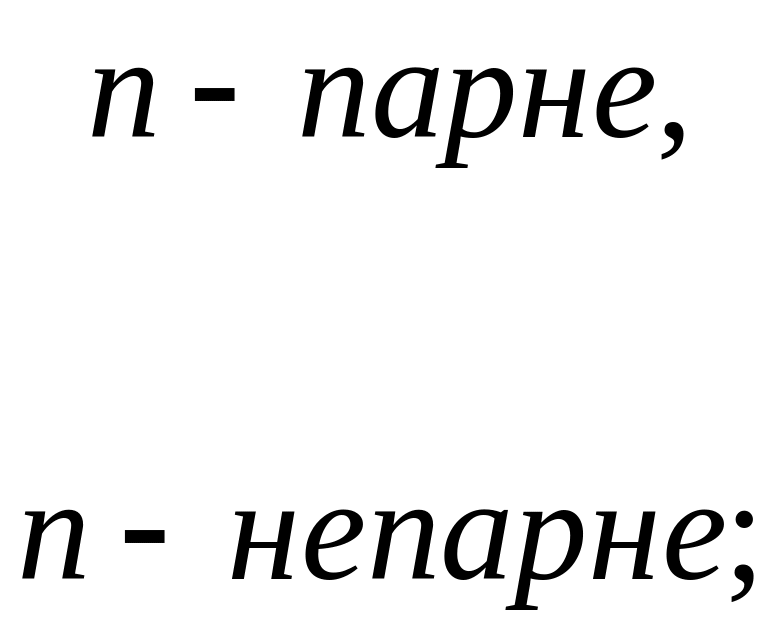
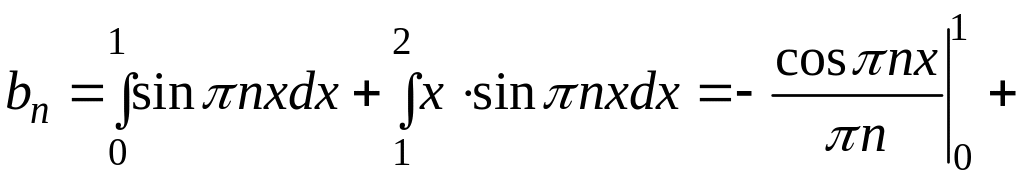
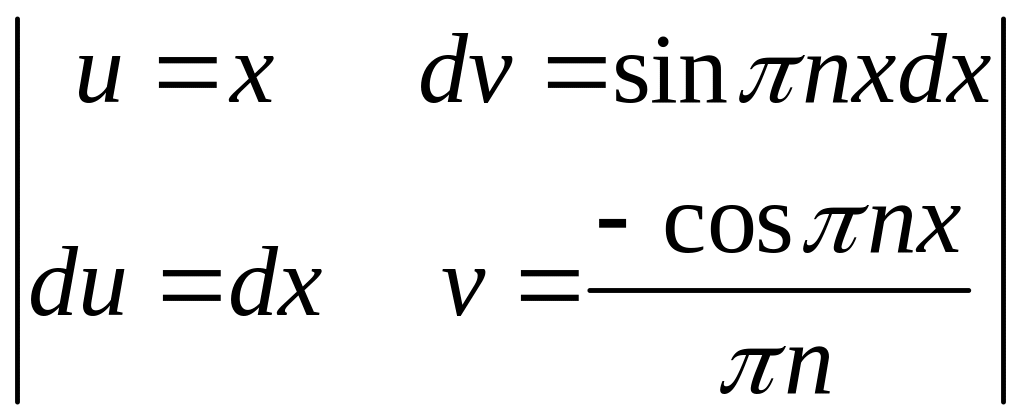
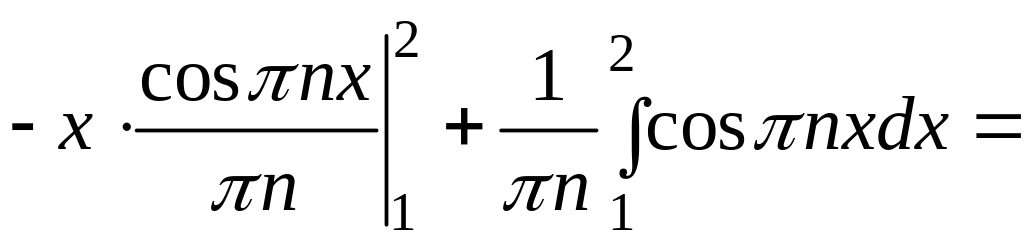

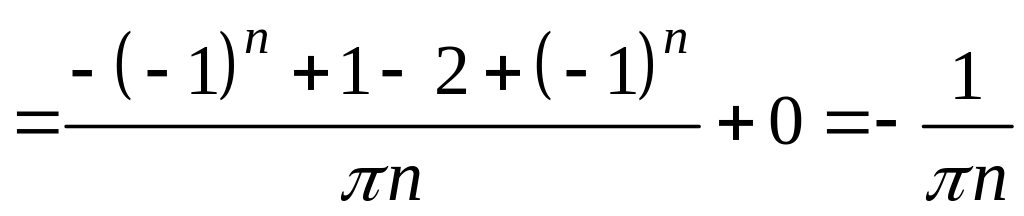 .
.
4. Запишіть відповідь.
Шуканий розклад даної функції має вигляд
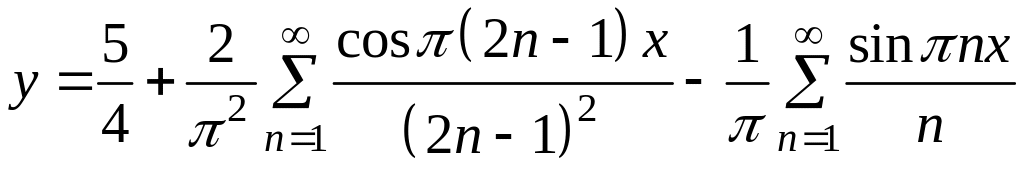 .
.
Приклад
11.19. Розкласти в ряд Фур’є функцію
![]()
1. Зробіть графік даної функції.
Зобразимо графік функції, одержаної періодичним продовженням функції на всю числову вісь.
(графік)
Проаналізуйте функцію і оберіть потрібні формули для подальшого розв’язування прикладу.
Для даної функції зручно застосувати комплексну форму ряду Фур’є (11.17)
3. Знайдіть коефіцієнти ряду Фур’є.
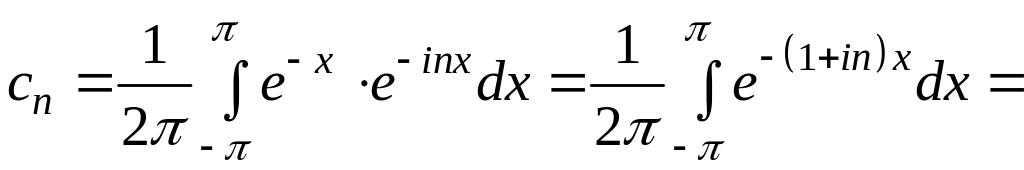
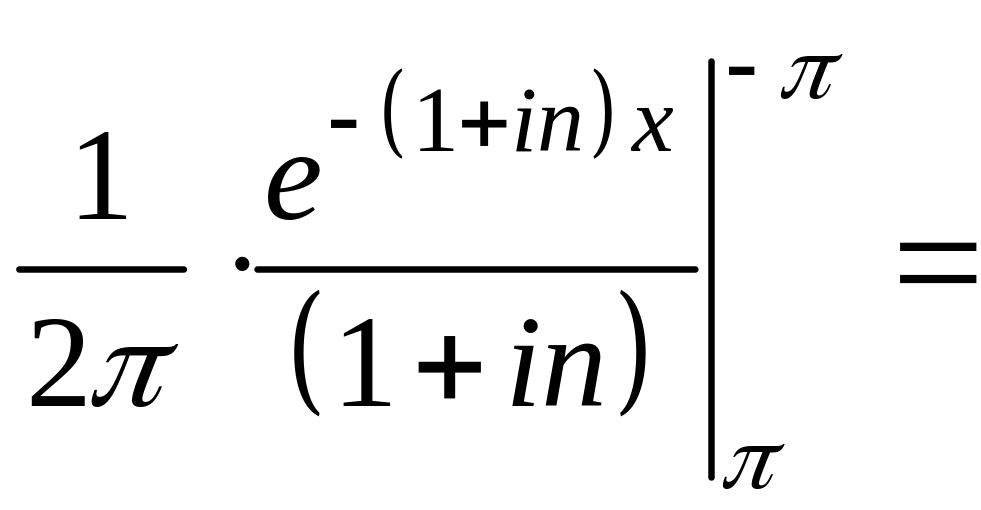
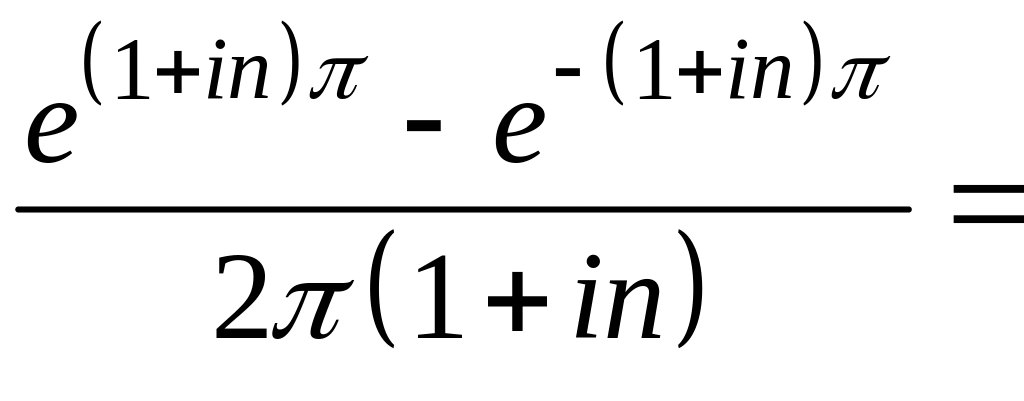
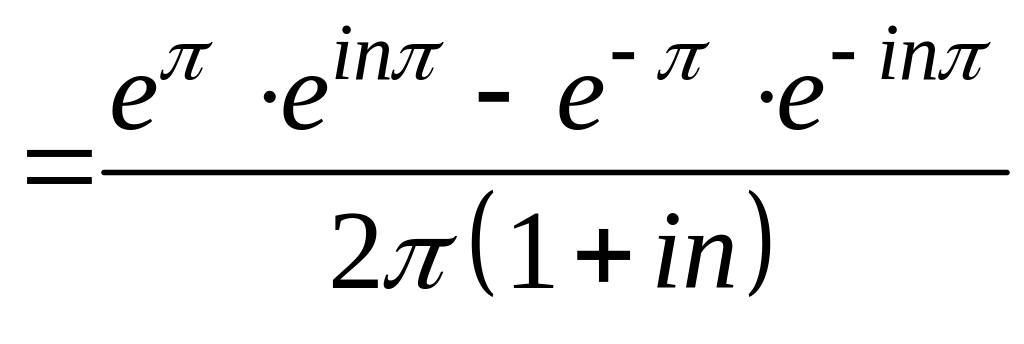 .
.
Зауважимо,
що за формулами Ейлера
![]() .
.
Отже,
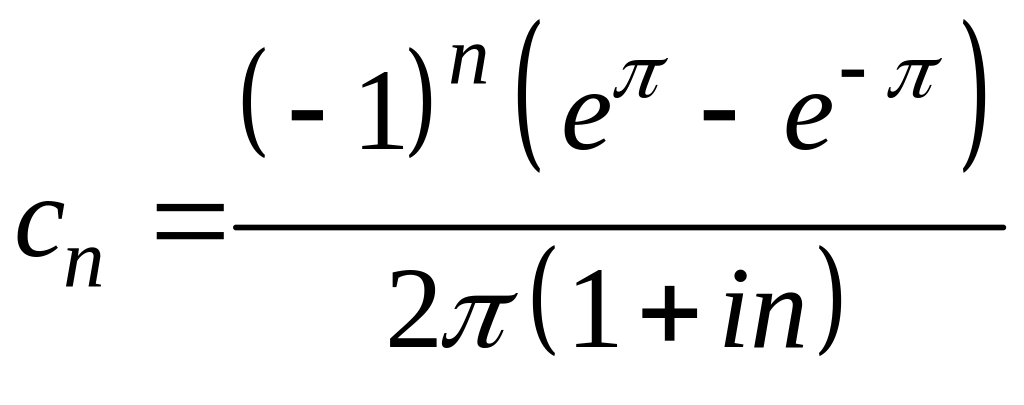 .
.
4. Запишіть відповідь.
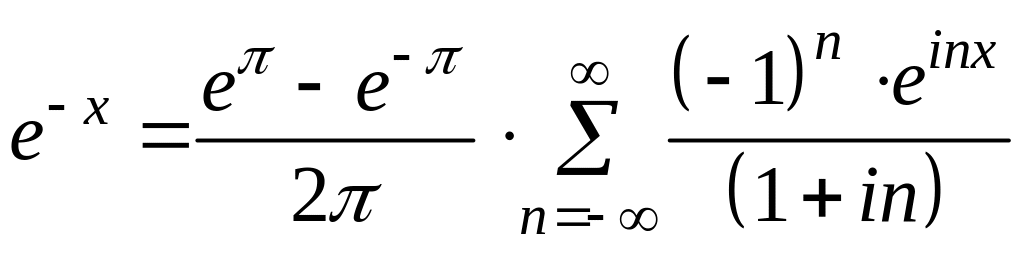 .
.
Зауваження.
Щоб перетворити отриманий ряд в
комплексній формі до звичайного
тригонометричного ряду Фур’є (якщо це
потрібно), слід об’єднати доданки з
індексами
і
![]() і замінити у підсумку за формулами
Ейлера показникові функції тригонометричними:
і замінити у підсумку за формулами
Ейлера показникові функції тригонометричними:

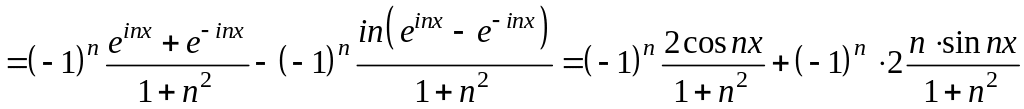 ,
,
![]()
Із самої
формули ряду в комплексній формі при
![]() отримаємо значення
отримаємо значення
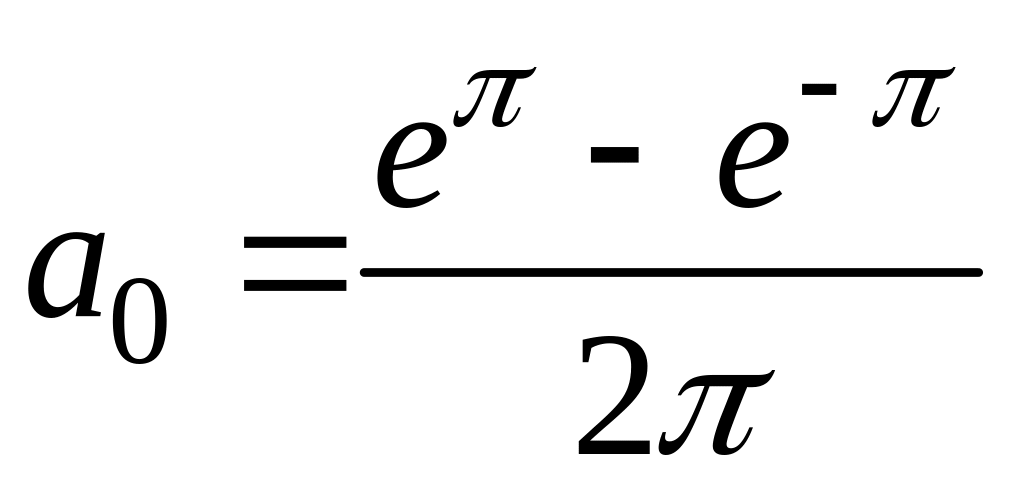 .
.
Таким
чином,
 .
.
Приклад
11.20. Розкласти в ряд Фур’є функцію
![]() .
Користуючись отриманим розкладом,
знайти суму
.
Користуючись отриманим розкладом,
знайти суму
![]() ряду
ряду
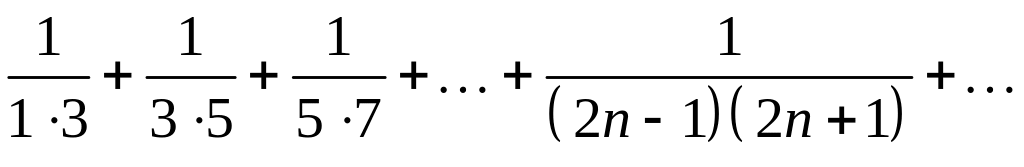 .
.
1. Зробіть графік даної функції.
(графік)
Зобразимо функцію та її періодичне продовження на всю числову вісь.
Проаналізуйте функцію і оберіть потрібні формули для подальшого розв’язування прикладу.
Дана
функція є парною, тому будемо застосовувати
формули (11.13). В інтервалі
![]() функція визначається формулою
функція визначається формулою
![]() .
.
3. Знайдіть коефіцієнти ряду Фур’є.
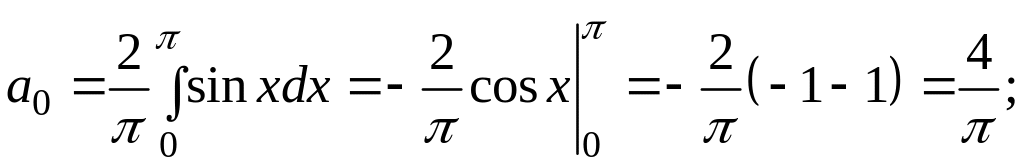
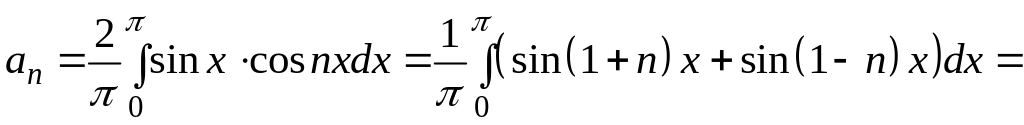
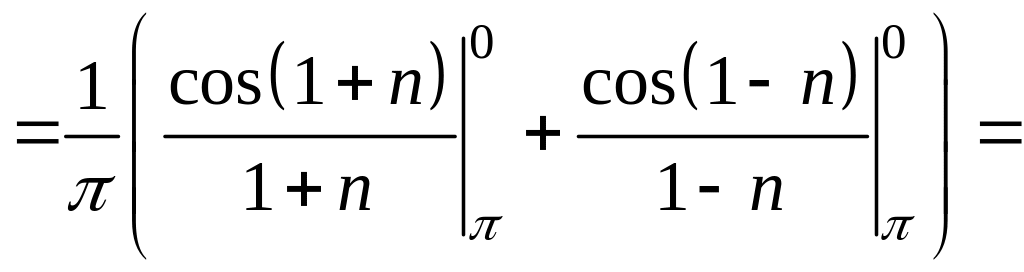
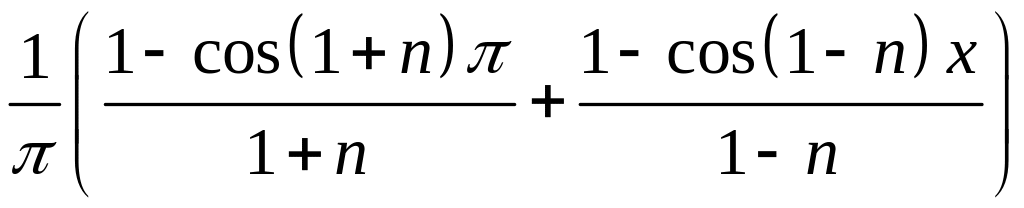 .
.
![]()
Якщо
парне, то
![]() і
і
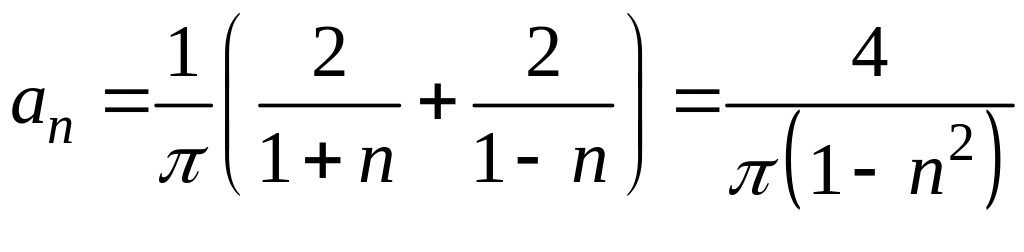 ,
,
![]() .
.
Якщо
непарне,
![]() ,
то
,
то
![]() і
і
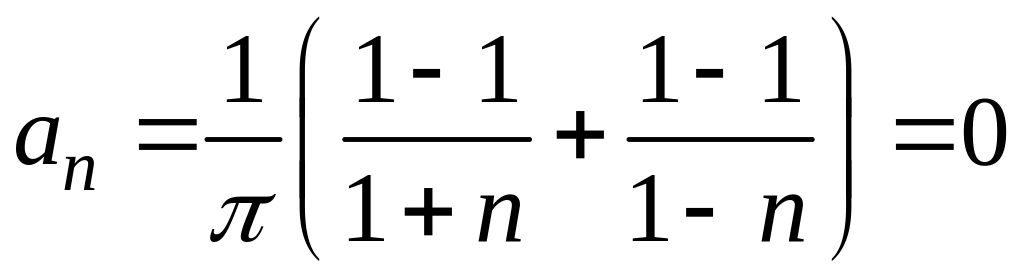 ,
,
![]() .
.
При
![]() отриманий тут загальний вираз для
не прийнятний, внаслідок чого коефіцієнт
отриманий тут загальний вираз для
не прийнятний, внаслідок чого коефіцієнт
![]() обчислюємо окремо, поклавши
в
загальну формулу (11.13).
обчислюємо окремо, поклавши
в
загальну формулу (11.13).
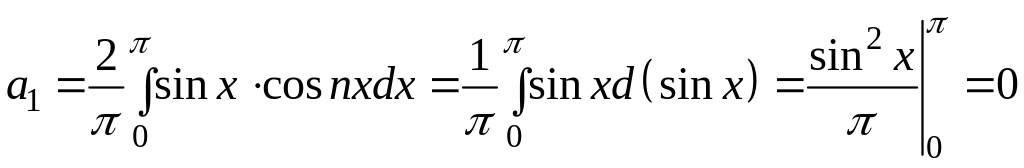 .
.
4. Запишіть шуканий ряд Фур’є.
Шуканий розклад:
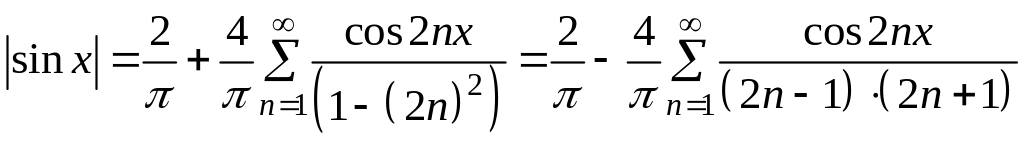 .
.
5. Знайдіть суму заданого в умові числового ряду.
При отриманий розклад перетворюється в рівність
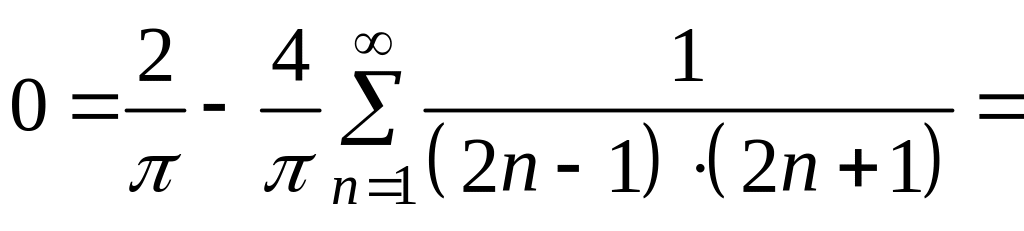
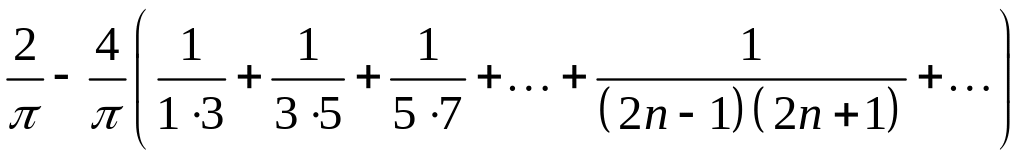 ,
звідки і визначається сума числового
ряду, вказаного в умові:
,
звідки і визначається сума числового
ряду, вказаного в умові:
![]() ,
,
![]() .
.
Зауваження. У цьому прикладі, як і у прикладі 11.20, виявилося, що для заданої функції один із коефіцієнтів ряду не можливо було обчислити за загальною формулою. Тому при розкладанні функції в ряд Фур’є після знаходження загальних виразів для коефіцієнтів і слід перевірити, чи будуть вони прийнятні при всіх значеннях . Для тих значень , при яких ці вирази втрачають сенс, необхідно обчислювати відповідні коефіцієнти окремо, підставляючи ці вилучені значення в загальні формули Фур’є.
Приклад
11.21. Розкласти функцію
![]() ,
,
в неповні ряди Фур’є які містять тільки
косинуси, або тільки синуси
,
,
в неповні ряди Фур’є які містять тільки
косинуси, або тільки синуси
1. Зробіть графік функції для розкладання її в ряд Фур’є по косинусам.
(графік)
Продовжимо
задану функцію на відрізок
![]() парним чином
парним чином
![]() .
Одержану функцію продовжимо на всю
числову вісь з періодом
.
Одержану функцію продовжимо на всю
числову вісь з періодом
![]() .
.
2. З’ясуйте, які формули будете застосовувати.
Далі
скористаємося формулами (11.13) розкладання
в ряд Фур’є парної функції з періодом
![]() .
.
3. Знайдіть коефіцієнти Фур’є.
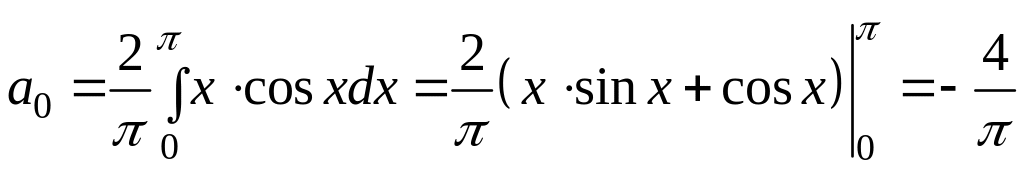
(для обчислення інтеграла, тут і далі будемо використовувати інтегрування частинками).
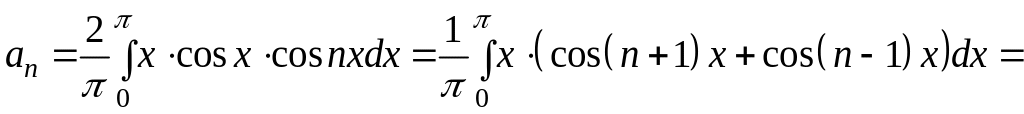
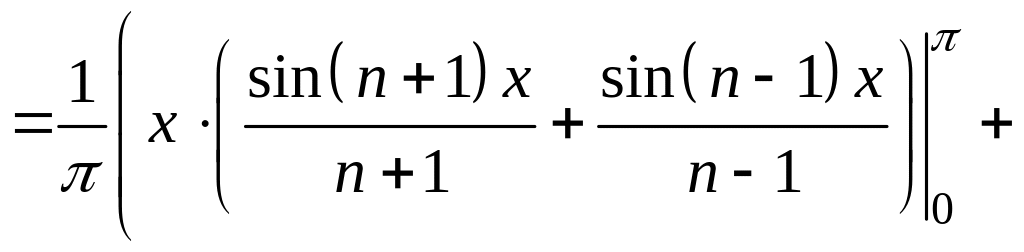
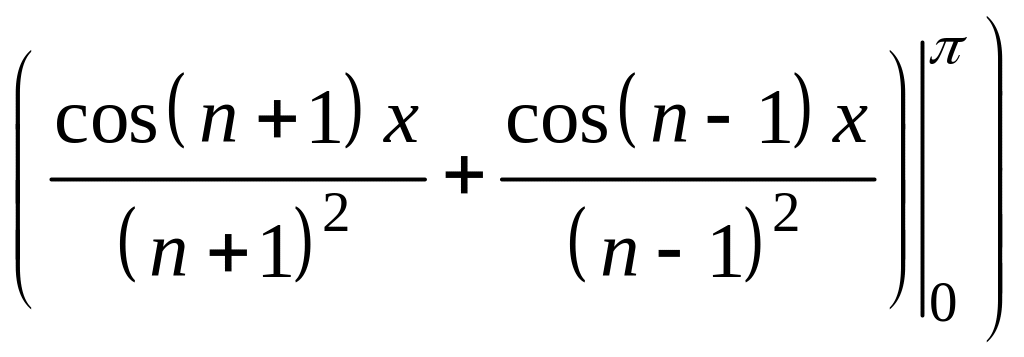 .
.
Якщо
![]() ,
,
то
,
,
то
![]() і
і
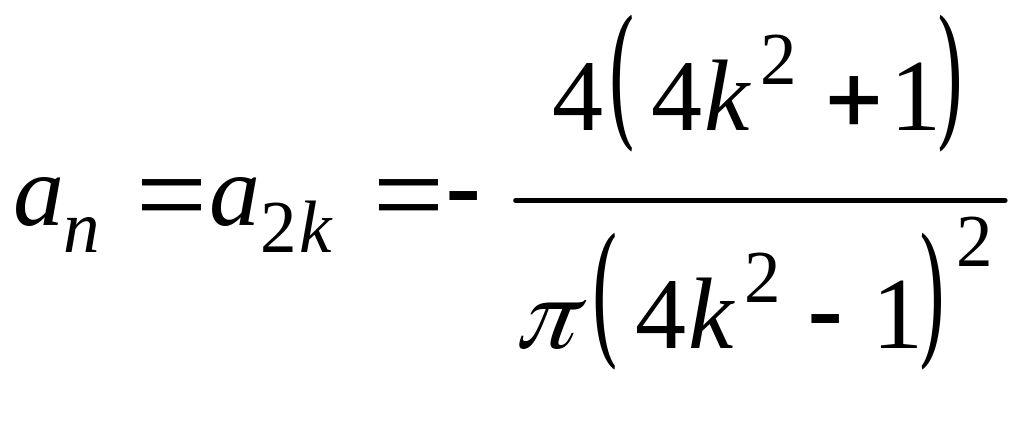 .
.
Якщо
![]() ,
,
,
,
![]() і
і
![]() .
.
Коефіцієнт обчислюємо окремо:
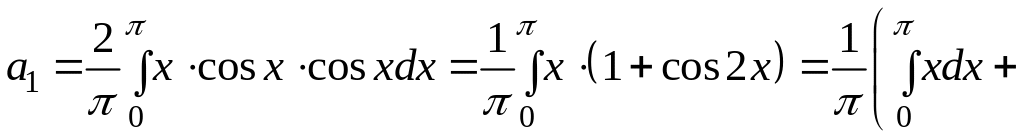
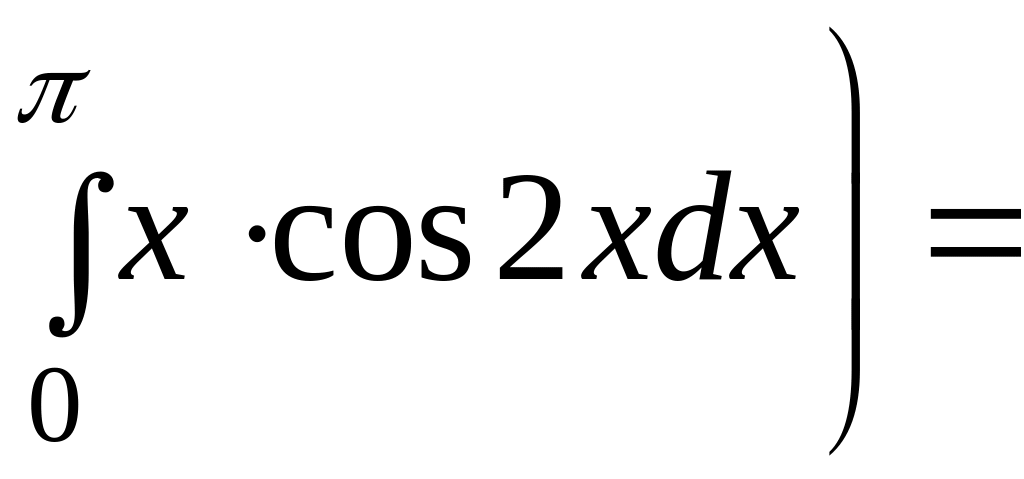
 .
.
4. Запишіть розклад функції в ряд Фур’є косинусам.
Таким
чином,
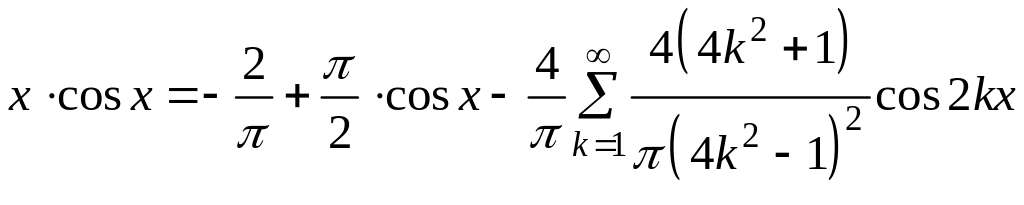 ,
,
![]() .
.
5. Зробіть графік функції для розкладання її в ряд Фур’є по синусам.
Продовжимо
задану функцію на відрізок
непарним чином та періодично продовжимо
на всю числову вісь
![]() .
.
(графік)
6. З’ясуйте, які формули будете застосовувати.
Далі скористаємося формулами (11.14) розкладання в ряд Фур’є непарної функції з періодом .
7. Знайдіть коефіцієнти Фур’є.
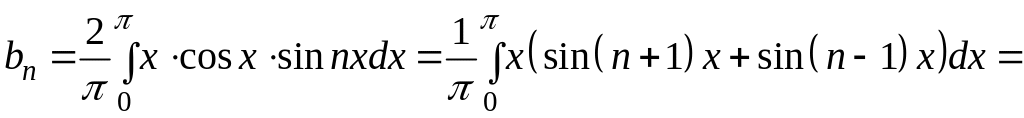
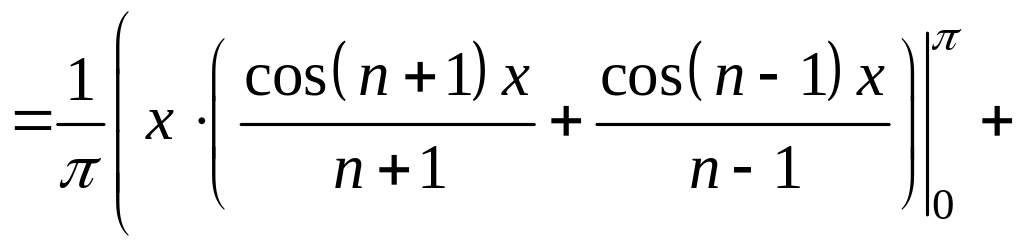
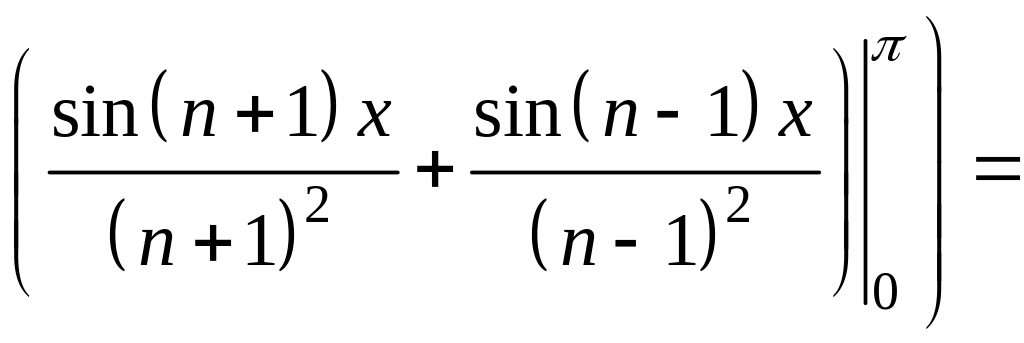
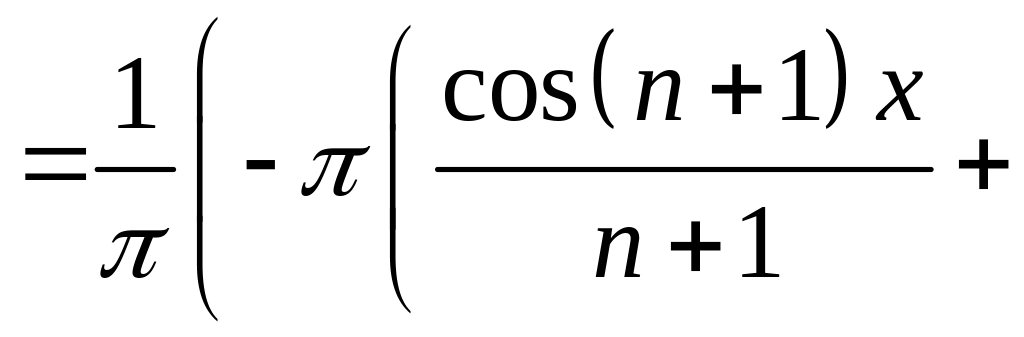
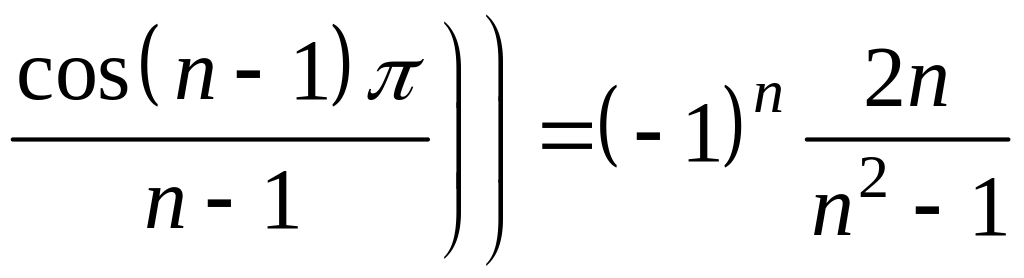 ,
.
,
.
Коефіцієнт
![]() обчислимо окремо:
обчислимо окремо:

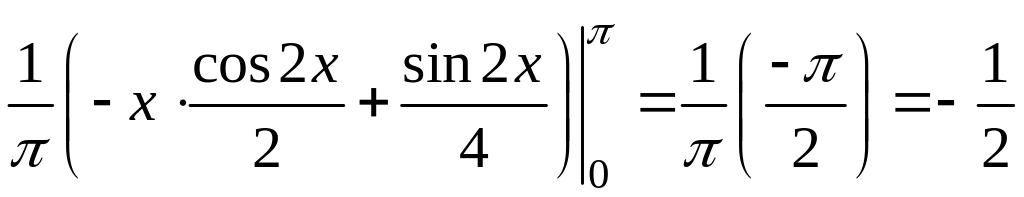 .
.
8. Запишіть розклад функції в ряд Фур’є по синусам.
Отже,
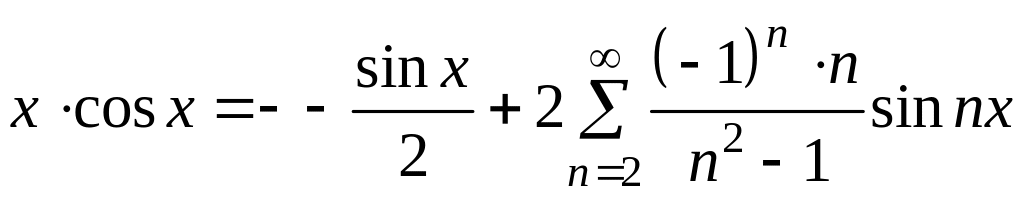 ,
.
,
.
