Алгоритм визначення області збіжності степеневих рядів.

1. З’ясуйте, за якою формулою слід знаходити радіус збіжності , і знайти його.

2. Записати інтервал збіжності.

3. Дослідити збіжність ряду на кінцях інтервалу збіжності (якщо або ):

Якщо , то ряд збігається тільки в точці .

Якщо , то інтервал збіжності

4. Записати відповідь.

Приклад 11.10. Визначити область збіжності ряду

1. З’ясуйте, за якою формулою слід знаходити радіус збіжності даного ряду.

Для даного ряду . Знайдемо радіус збіжності за формулою (11.1).

2. Знайдіть радіус збіжності.

Оскільки , маємо .

3. Запишіть відповідь.

Рівність означає, що ряд збігається тільки в точці .

Приклад 11.11. Визначити область збіжності ряду

1. З’ясуйте, за якою формулою слід знаходити радіус збіжності даного ряду.

Для даного ряду . Знайдемо радіус збіжності за формулою (11.2).

2. Знайдіть радіус збіжності.

.

3. Запишіть відповідь.

Якщо , то область збіжності ряду співпадає з інтервалом збіжності і є такою: .

Приклад 11.12. Визначити область збіжності ряду

1. З’ясуйте, за якою формулою слід знаходити радіус збіжності даного ряду.

Для даного ряду .

Будемо знаходити радіус збіжності за формулою (11.1).

2. Знайдіть радіус збіжності.

Оскільки , маємо

3. Запишіть інтервал збіжності.

Інтервал збіжного ряду .

4. Дослідіть збіжність ряду на кінцях інтервалу збіжності.

Дослідимо збіжність ряду при .

При маємо числовий ряд , який можна можна досліджувати за ознаками знакододатного ряду.

Застосуємо до нього граничну ознаку порівняння – порівняємо з рядом .

.

Оскільки ряд збіжний, то ряд теж збіжний .

При маємо числовий знакозмінний ряд 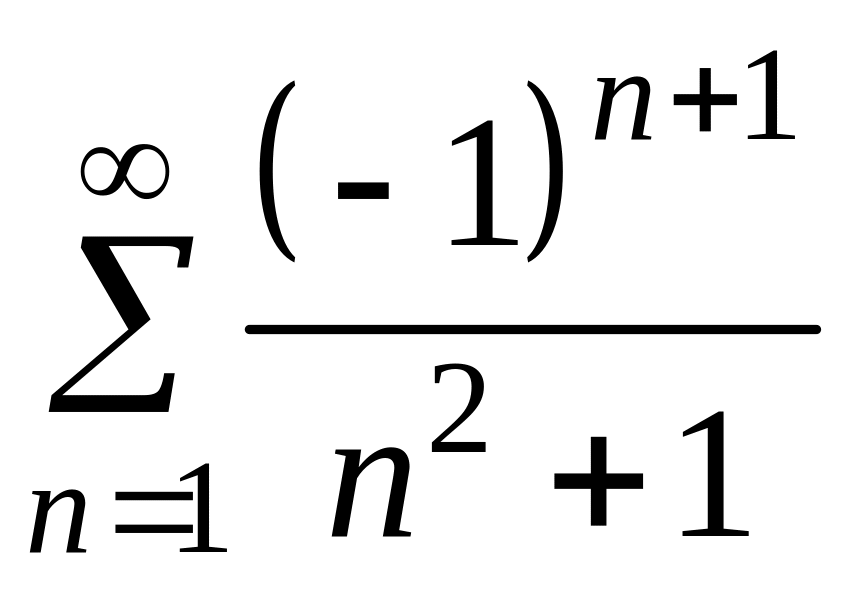. За достатньою ознакою збіжності знакозмінних рядів він є збіжним.

5. Запишіть відповідь.

Областю збіжності ряду є інтервал , до якого приєднуються точки і .

У підсумку, областю збіжності є .

Приклад 11.13. Визначити область збіжності ряду

1. З’ясуйте, за якою формулою слід знаходити радіус збіжності даного ряду.

Це ряд виду (2). (див. 11.2 Степеневі ряди)

Для даного ряду .

Будемо знаходити радіус збіжності за формулою (11.1).

2. Знайдіть радіус збіжності.

Оскільки , то .

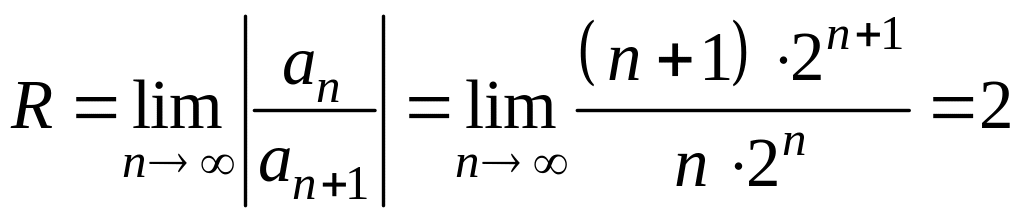3. Запишіть інтервал збіжності.

За умовою , тому інтервал збіжності такий: або .

4. Дослідіть збіжність ряду на кінцях інтервалу збіжності.

Дослідимо збіжність ряду при і .

При маємо числовий знакододатний ряд . Це гармонічний ряд, який є розбіжним.

При отримуємо знакопочережний числовий ряд

.

До нього застосуємо ознаку Лейбніца:

1) - виконується;

2) - виконується;

Оскільки обидві умови ознаки Лейбніца виконуються, то знакопочережний ряд збігається.

5. Запишіть відповідь.

Областю збіжності заданого ряду й інтервал , до якого приєднується точка .

Отже, область збіжності: .

Приклад 11.14. Визначити область збіжності ряду

1. З’ясуйте, за якою формулою слід знаходити радіус збіжності даного ряду.

Даний ряд відноситься до виду (4). (див. 11.2 Степеневі ряди)

, тому радіус збіжності знаходимо за формулою (11.4).

2. Знайдіть радіус збіжності.

Оскільки , то .

3. Запишіть інтервал збіжності.

За умовою , тому інтервал збіжності такий: .

4. Дослідіть збіжність ряду на кінцях інтервалу збіжності.

При маємо числовий знакододатний ряд . Це узагальнений гармонічний ряд , який при збігається.

При отримаємо такий же числовий ряд , який є збіжним.