11 Ряди

11.1 Числові ряди

Необхідна умова збіжності числового ряду:

якщо ряд збігається, то . (11.1)

Достатня умова розбігається числового ряду:

якщо , то ряд розбігається. (11.2)

11.1.1 Числові знакододатні ряди ,

Рекомендації до застосування достатніх ознак збіжності числових знакододатних рядів:

Ознака Даламбера:

Якщо , перевірити виконання необхідної умови збіжності.

Радикальна ознака Коші:

Якщо , перевірити виконання необхідної умови збіжності.

Друга гранична ознака порівняння рядів:

(порівняти з рядом....

Інтегральна ознака Коші:

Див. розділ «Невласні інтеграли».

В інших випадках застосовуеться перша ознака порівняння рядів (1) і (2), , :

Якщо ряд (2) збіжний, то ряд (1) також збіжний;

Якщо ряд (1) розбіжний, то ряд (2) також розбіжний.

Алгоритм дослідження збіжності числових знакододатних рядів.

1. Перевірити виконання необхідної умови збіжності.

2. У разі її виконання застосувати певну достатню умову збіжності (орієнтуючись рекомендаціями на стор. 1).

3. Якщо необхідна умова збіжності не виконується, то ряд є розбіжним.

Приклад 11.1 Дослідити збіжність ряду

1. Перевірте виконання необхідної умови збіжності.

.

.

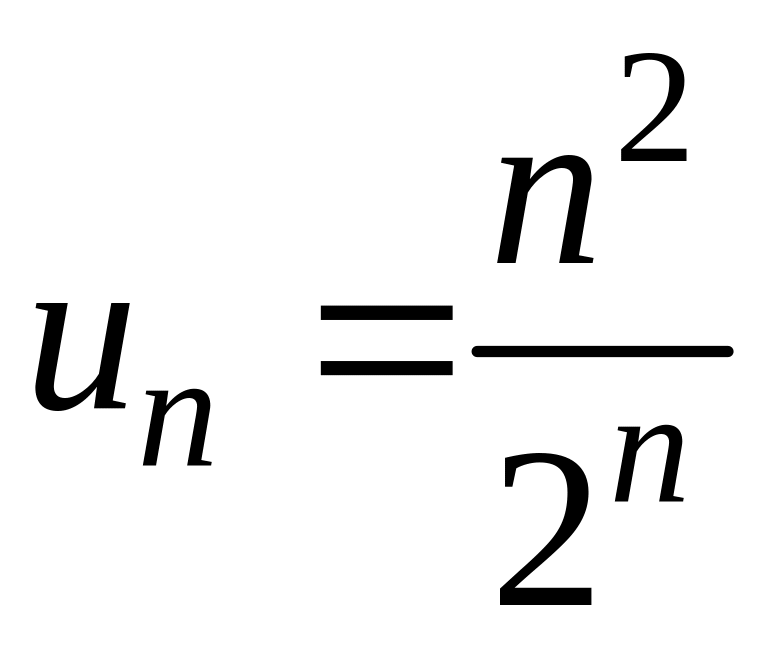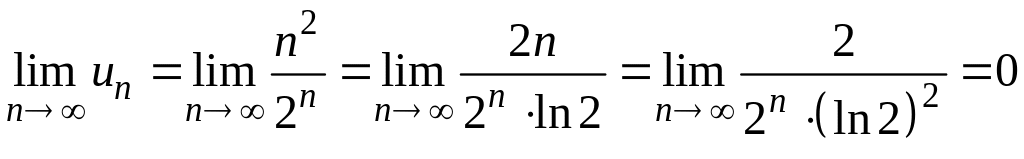Отже, необхідна умова збіжності виконується.

2. З’ясуйте, яку достатню ознаку збіжності слід використати для даного ряду.

Згідно рекомендаціям, для рядів, що містять показникові функцію(у нас ) слід застосувати ознаку Даламбера.

3. Застосуйте обрану ознаку збіжності.

Знаючи , знайдемо наступній за ним -й член, замінюючи у виразі -го члена через :

.

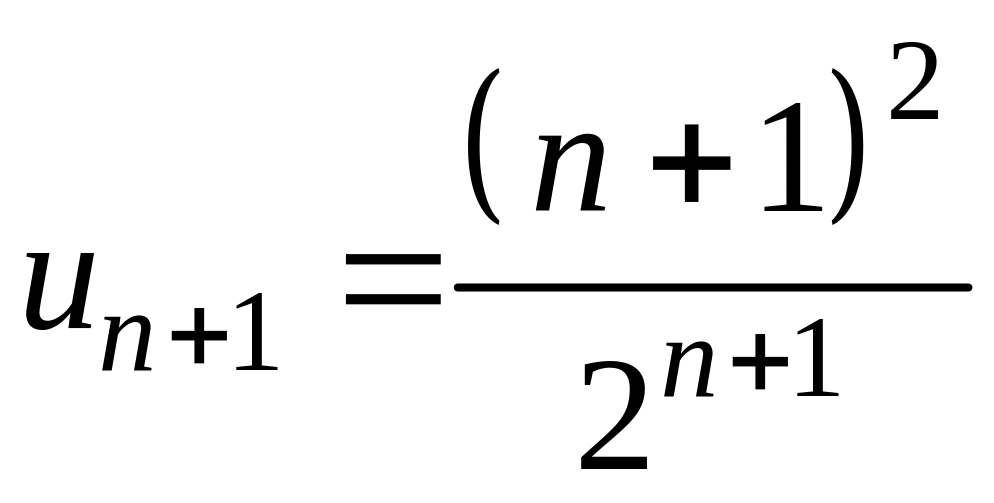Потім шукаємо границю відношення наступного члена до попереднього при .

(для обчислення можна застосувати, наприклад, правило Лопіталя)

4. Запишіть відповідь.

Отже, за ознакою Даламбера заданий ряд збігається.

Приклад 11.2 Дослідити на збіжність ряд

1. Перевірте виконання необхідної умови збіжності.

.

, оскільки при високого порядку є нескінченно великою більш високого порядку ніж .

2. Запишіть відповідь.

Оскільки необхідна умова збіжності рядів не виконується, то ряд розбігається.

Приклад 11.3 Дослідити на збіжність ряд

1. Перевірте виконання необхідної умови збіжності.

.

, оскільки при є нескінченно великою більш високого порядку, ніж .

2. З’ясуйте, яку достатню ознаку збіжності слід використати для даного ряду.

Згідно рекомендаціям, для рядів, які містять показникову функцію і величина з факторіалом слід застосувати ознаку Даламбера.

3. Застосуйте обрану ознаку збіжності.

Знаючи , знайдемо наступній за ним -й член, для чого у виразі -го члена замінимо на :

.

Тепер шукаємо границю відношення наступного члена до попереднього при

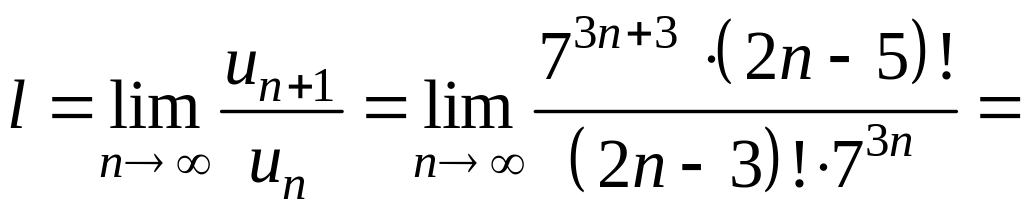
4. Запишіть відповідь.

За ознакою Даламбера заданий ряд збігається.

Приклад 11.4 Дослідити на збіжність ряд

1. Перевірте виконання необхідної умови збіжності.

.

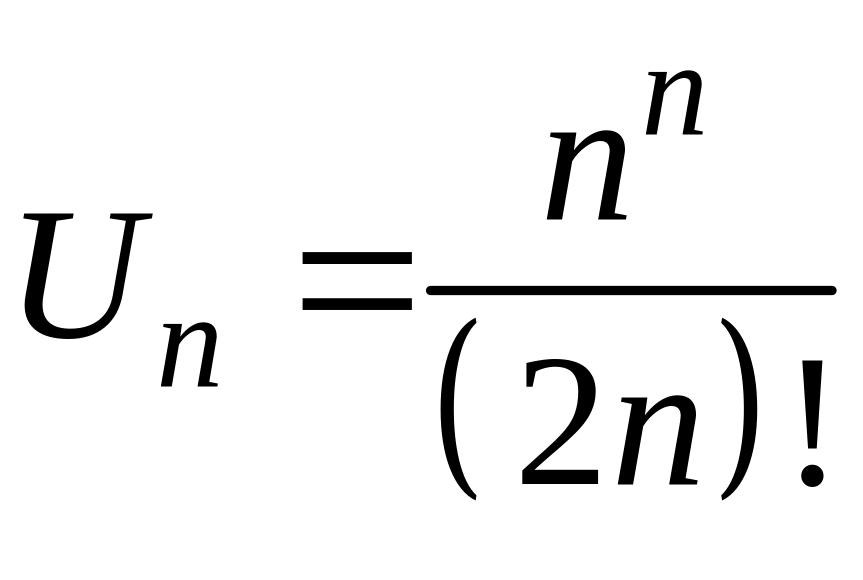Знайти важко тому відразу до достатніх ознак збіжності.

2. З’ясуйте, яку достатню ознаку збіжності слід використати для даного ряду.

Згідно рекомендаціям, обираємо ознаку Даламбера.

3. Застосуйте обрану ознаку збіжності.

Оскільки , то .

.

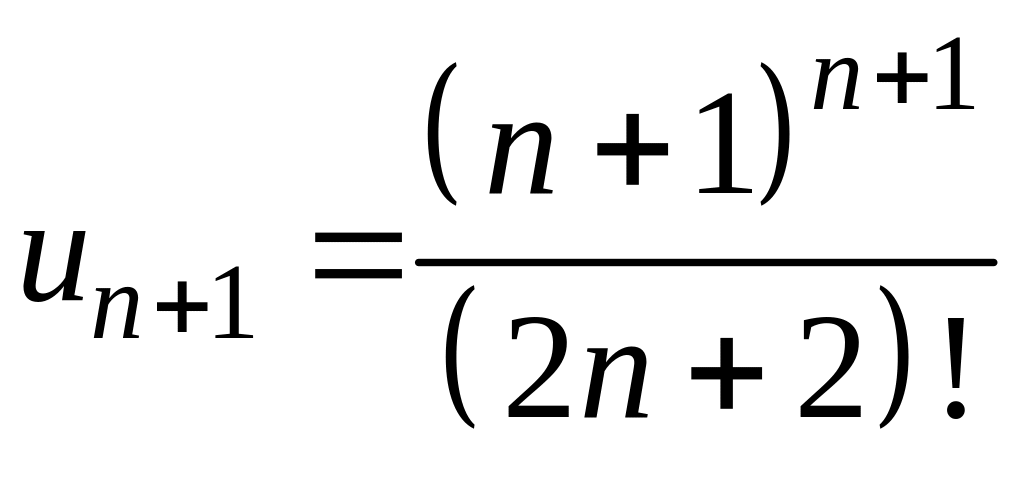(для обчислення застосували правило Лопіталя)

4. Запишіть відповідь.

За ознакою Даламбера заданий ряд збігається.

Приклад 11.5 Дослідити на збіжності ряд

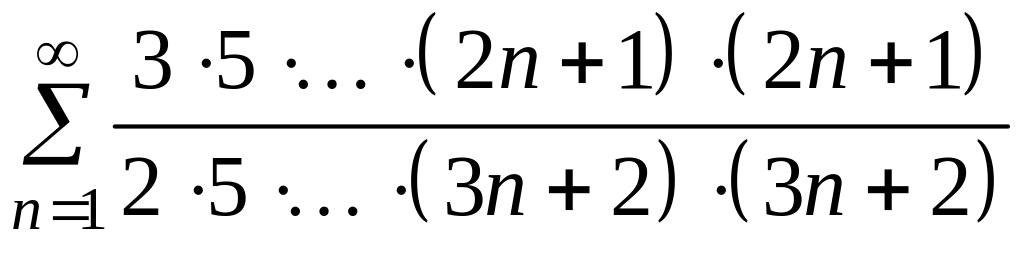
1. Перевірте виконання необхідної умови збіжності.

Рекомендації не містять такого випадку. Спробуємо застосувати ознаку Даламбера.

2. З’ясуйте, яку достатню ознаку збіжності слід використати для даного ряду.

.

.

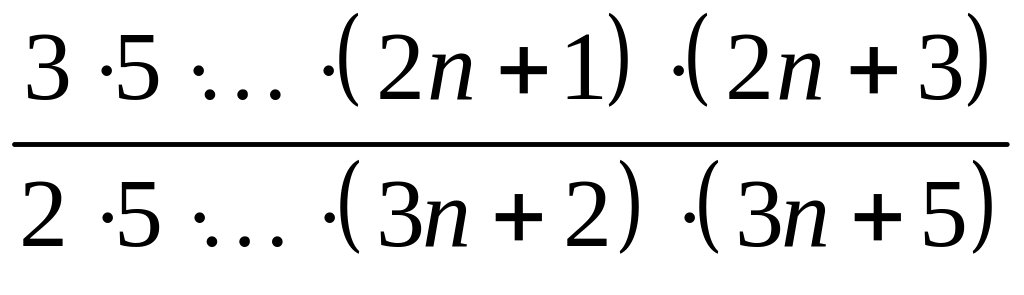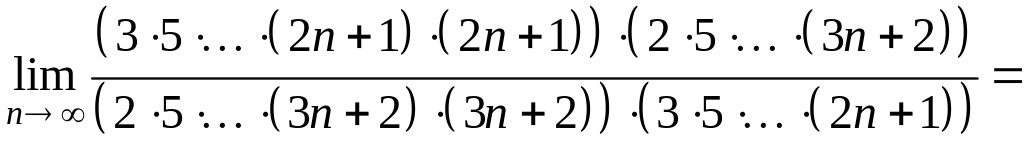
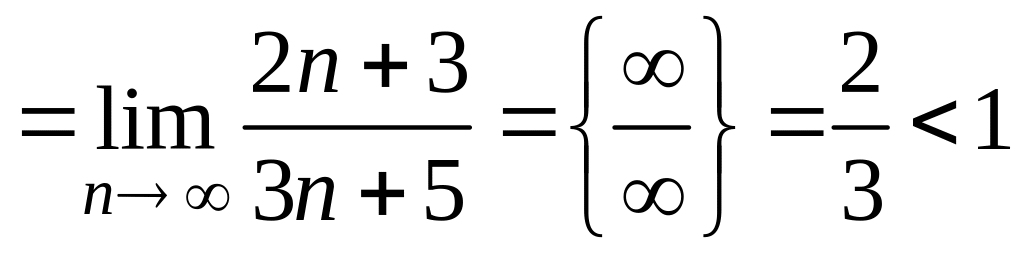3. Запишіть відповідь.

За ознакою Даламбера заданий ряд збігається.