Методика ознайомлення з дробами
2.1. Поняття дробу як кількох рівних частин цілого
Наведемо фрагмент уроку по ознайомленню з поняттям «дріб» через поділ цілого на рівні частини.
Підготовча робота
Вчитель послідовно показує кілька чисел і пропонує охарактеризувати їх одним-двома словами (1, 3, 5, 7, 9 –одноцифрові, непарні; 37, 49, 92, 99 – двоцифрові; 10, 20 30, 300, 600, 1200 – круглі числа, 357, 4900, 23506 – багатоцифрові числа).
- Всі ці числа можна назвати одним словом – натуральні. Вони використовуються при лічбі предметів, при вимірюванні величин. На сьогоднішньому уроці ми познайомимося з деякими іншими числами, які називаються дробовими або просто дробами. Ці числа використовуються при позначенні частин цілого (однієї чи кількох). Ціле може бути геометрична фігура, маса предмета, відстань, швидкість, тобто якась величина. Дробові числа виникли якраз при вимірюванні величин. Наприклад, у повсякденному житті ми часто кажемо півкілограма, півметра, три чверті години, третина поля. З деякими із дробових чисел ви уже знайомі. Це записи певної частини цілого.
Ознайомлення з поняттям «дріб»
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||| |
|||||||||||||||||||||||||||||||||||||||||||||||||||| |
На скільки рівних частин поділено прямокутник?
Скільки таких частин не зафарбовано?
Як це записати цифрами? ( ).
Як читається цей запис? (Одна третя)
Що означає число 3? (Що прямокутник поділено на 3 рівні части).
Що означає число 1? (Що взята одна така частина).
Скільки частинок зафарбовано? (дві).
За допомогою цифр зафарбовані частинки записуються так:
.
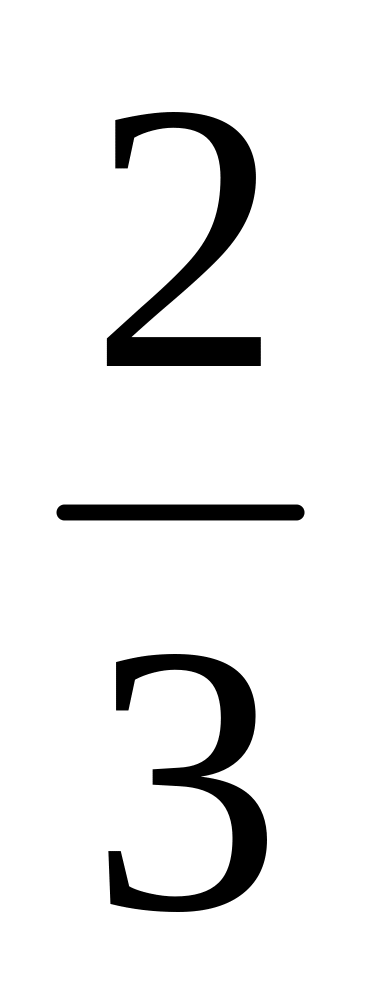Читається : дві третіх.
І так ще кілька подібних прикладів з використанням наочності.
Ми записали ряд чисел, що називаються дробовими. Число
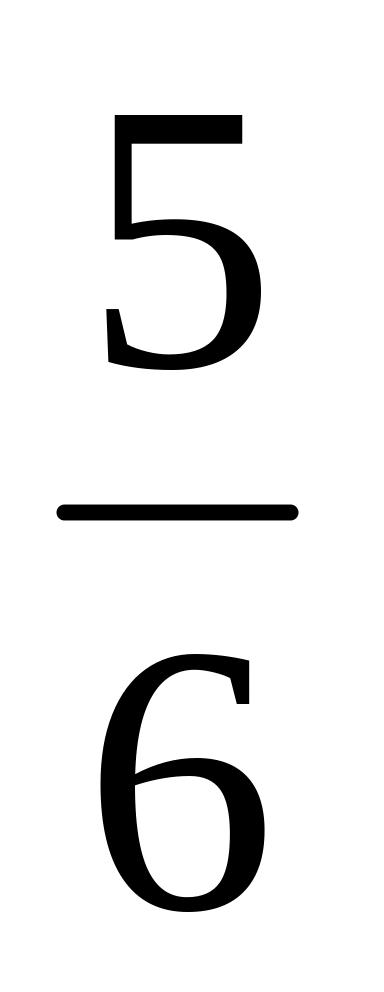- дріб. Числа 5 і 6 розділені рискою, яка
називається рискою дробу. Число під
рискою дробу називається знаменник
дробу. Знаменник дробу показує на
скільки рівних частин поділено ціле.
Число 5 над рискою дробу називається
чисельник
дробу. Воно показує скільки таких рівних
частин взято.
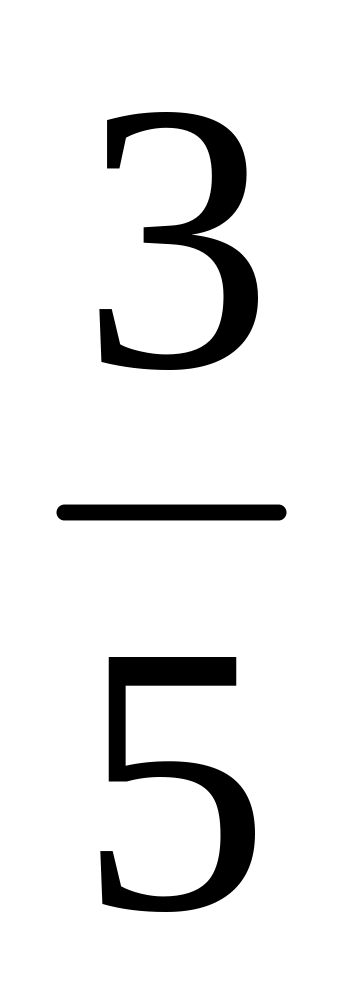
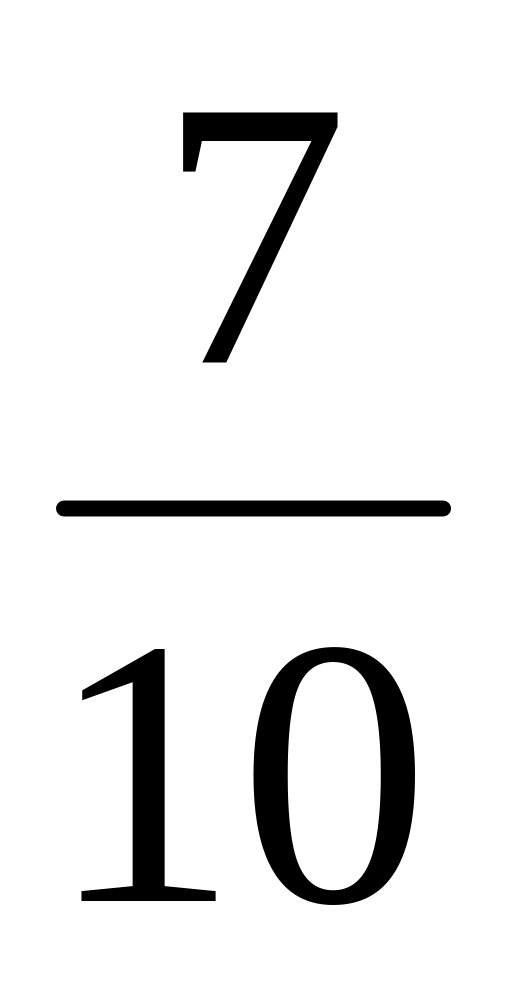
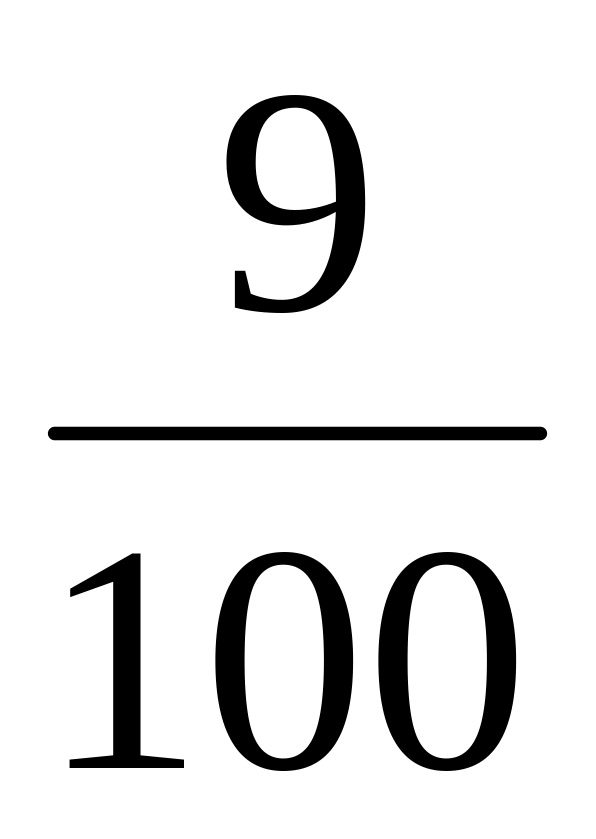
Прочитайте дроби.
Назвіть знаменник третього дробу; останнього дробу. Що показує знаменник дробу?
Назвіть чисельник четвертого дробу; першого дробу. Що показує чисельник дробу?
Що показує знаменник другого дробу? Чисельник другого дробу?
- А що ми будемо мати, коли чисельник буде дорівнювати знаменнику? ( Ми будемо мати ціле).
- У цьому випадку кажуть, що дріб дорівнює 1.
2.2. Поняття дробу як частки двох чисел
1) Підготовча робота
- Що означає чверть кілограма? Як її знайти? Скільки це становить? ( 1000г : 4 = 250г).
- Що означає три чверті кілограма? Як знайти? Скільки це становить? (1000г : 4 · 3 = 750г).
2) Розв’язування задачі:
4 хлопчики впіймали 3кг риби і поділили її порівну. Скільки риби отримав кожний хлопчик?
-
1 кг
1кг
1кг
що потрібно зробити, щоб відповісти на запитання задачі? (Треба кількість риби поділити на кількість хлопчиків, тобто, кожний з хлопчиків одержав по 3 : 4 (кг) риби).
Не перетворюючи кілограми в грами, число 3кг поділити на 4 ми не можемо. Ми бачимо, що риба розділена в мішечки по кілограму в кожному. Будемо ділити рибу з кожного мішечка окремо. Скільки кілограмів риби одержить кожний хлопчик з першого мішечка? ( кг). З другого також кг і з третього також кг. Кожний хлопчик одержить по
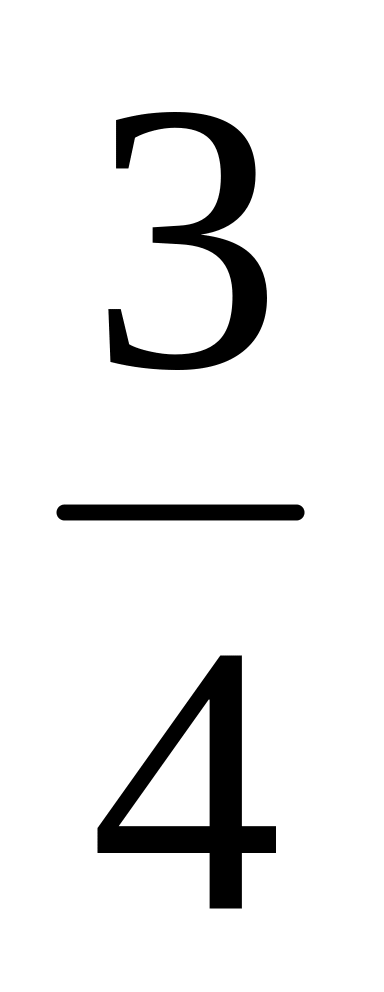кг
риби. Ми можемо розв’язання задачі
записати так: 3 : 4 =
(кг). Обчислимо, скільки це буде у грамах.
1кг = 1000г. 1000г : 4 · 3 = 750 г.Отже частку чисел 3 і 4 можна записати у вигляді дробу. Число, яке ділимо, записуємо у чисельник. Число, на яке ділимо, записуємо у знаменник. Так можна записувати не тільки частку чисел, які не діляться одне на одного, але і частку будь-яких двох чисел. Запишіть у вигляді дробу частку чисел 7 і 9; 8 і 12.